【集合论】关系幂运算 ( 关系幂运算 | 关系幂运算示例 | 关系幂运算性质 )
一、关系幂运算 、二、关系幂运算示例 、三、关系幂运算性质
一、关系幂运算
关系 R R R 的 n n n 次幂定义 :
R ⊆ A × A , n ∈ N R \subseteq A \times A , n \in N R⊆A×A,n∈N
{ R 0 = I A R n + 1 = R n ∘ R ( n ≥ 0 ) \begin{cases} R^0 = I_A & \\ R^{n +1} = R^n \circ R & ( n \geq 0 ) \end{cases} {R0=IARn+1=Rn∘R(n≥0)
关系 R R R 是 集合 A A A 上的 二元关系 , R R R 的 0 0 0 次幂 R 0 R^0 R0 是恒等关系 I A I_A IA , 关系 R R R 的 n + 1 n + 1 n+1 次幂等于 R n + 1 = R n ∘ R R^{n + 1} = R^n \circ R Rn+1=Rn∘R 其中 n ≥ 0 n \geq 0 n≥0 ;
R 1 = R 0 ∘ R = R R^1 = R^0 \circ R = R R1=R0∘R=R , 恒等关系与 关系 R R R 逆序合成 , 结果还是关系 R R R , 这个关系 R R R 可以是任意关系 ;
恒等关系就是 集合 A A A 中每个元素自己跟自己有关系 ;
关系 R R R 幂运算结果 R n R^n Rn 关系 也是集合 A A A 上的二元关系 , 因此有 R n ⊆ A × A R^n \subseteq A \times A Rn⊆A×A
关系 R R R 的 n n n 次幂 , 就是 n n n 个 R R R 关系逆序合成 :
R n = R ∘ R ∘ ⋯ ∘ R ⏟ n 个 R 逆 序 合 成 R^n = \begin{matrix} \underbrace{ R \circ R \circ \cdots \circ R } \\ n 个 R 逆序合成 \end{matrix} Rn= R∘R∘⋯∘Rn个R逆序合成
二、关系幂运算示例
集合 A = { a , b , c } A = \{ a, b, c \} A={a,b,c} 关系 R R R 是 集合 A A A 上的二元关系 , R ⊆ A × A R \subseteq A \times A R⊆A×A ,
R = { < a , b > , < b , a > , < a , c > } R = \{ <a,b> , <b,a> , <a, c> \} R={<a,b>,<b,a>,<a,c>}
关系 R R R 的 幂集个数 : A A A 是有限集 , A A A 上的有序对个数是 3 × 3 = 9 3 \times 3 = 9 3×3=9 个 , A A A 上的二元关系个数 , 即有序对集合的幂集个数 , 是 2 3 × 3 = 512 2^{3\times 3} =512 23×3=512 个 ;
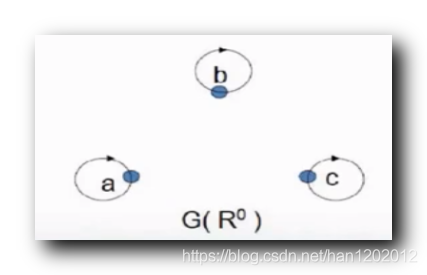
关系 R R R 的 0 0 0 次幂 : R 0 = I A R^0 = I_A R0=IA , R R R 关系的 0 0 0 次幂是恒等关系 , 关系图是每个顶点都有环 , 顶点之间没有关系 ;
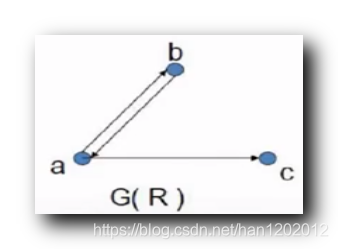
关系 R R R 的 1 1 1 次幂 : R 1 = R 0 ∘ R = R R^1 = R^0 \circ R = R R1=R0∘R=R , 恒等关系 I A I_A IA 与任何关系逆序合成 , 结果还是那个关系 ;
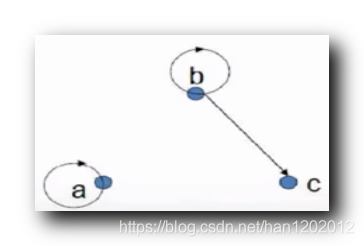
关系 R R R 的 2 2 2 次幂 :
R 2 = R 0 ∘ R = R ∘ R = { < a , b > , < b , a > , < a , c > } ∘ { < a , b > , < b , a > , < a , c > } = { < a , a > , < b , b > , < b , c > } \begin{array}{lcl}R^2 & = & R^0 \circ R \\\\ &=& R \circ R \\\\ &=& \{ <a,b> , <b,a> , <a, c> \} \circ \{ <a,b> , <b,a> , <a, c> \} \\\\ &=& \{ <a,a>, <b, b> , <b,c> \}\end{array} R2====R0∘RR∘R{<a,b>,<b,a>,<a,c>}∘{<a,b>,<b,a>,<a,c>}{<a,a>,<b,b>,<b,c>}
注意上述 ∘ \circ ∘ 运算时逆序合成 , 从后面的关系中合成前面的关系 ;
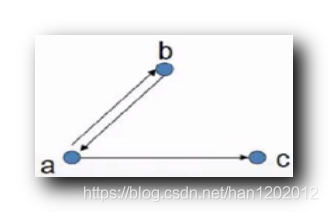
关系 R R R 的 3 3 3 次幂 : 与 R 1 R_1 R1 相同
R 3 = R 1 ∘ R = { < a , a > , < b , b > , < b , c > } ∘ { < a , b > , < b , a > , < a , c > } = { < a , b > , < a , c > , < b , a > } = R 1 \begin{array}{lcl}R^3 & = & R^1 \circ R \\\\ &=& \{ <a,a>, <b, b> , <b,c> \} \circ \{ <a,b> , <b,a> , <a, c> \} \\\\ &=& \{ <a,b>, <a, c> , <b,a> \} \\\\ &=& R^1 \end{array} R3====R1∘R{<a,a>,<b,b>,<b,c>}∘{<a,b>,<b,a>,<a,c>}{<a,b>,<a,c>,<b,a>}R1
关系 R R R 的 4 4 4 次幂 : 与 R 2 R_2 R2 相同
关系 R R R 的 5 5 5 次幂 : 与 R 1 R_1 R1 相同
关系 R R R 的 2 k 2k 2k 偶数次幂 ( k = 1 , 2 , ⋯ k=1,2, \cdots k=1,2,⋯ ) : 与 R 2 R_2 R2 相同
关系 R R R 的 2 k + 1 2k + 1 2k+1 奇数次幂 ( k = 0 , 1 , 2 , ⋯ k=0,1,2, \cdots k=0,1,2,⋯ ) : 与 R 1 R_1 R1 相同
三、关系幂运算性质
关系幂运算性质 :
关系 R R R 是 集合 A A A 上的关系 , R ⊆ A × A R \subseteq A \times A R⊆A×A , m , n m,n m,n 是自然数 , m , n ∈ N m,n \in N m,n∈N ; 关系幂运算有以下两个性质 :
R m ∘ R n = R m + n R^m \circ R^n = R^{m + n} Rm∘Rn=Rm+n
( R m ) n = R m n (R^m ) ^n = R^{m n} (Rm)n=Rmn
更多推荐
 已为社区贡献58条内容
已为社区贡献58条内容









所有评论(0)