常用的坐标系是右手系，ros中也是如下图：

坐标变换:

习惯上,我们表示一个物体的三维位置和朝向时,都会在其身上附一个随动的坐标系.所以描述一个物体在坐标系中的位置和朝向,总是可以等效为描述物体自身坐标系和别的坐标系之间的关系.

一般的坐标系转换主要为平移转换和旋转转换

可以看看 机器人坐标转换

齐次坐标 齐次坐标的理解 讲的不错。

公众号上的两篇文章：

干货 | 位置角度平移旋转，“乱七八糟”的坐标变换

另外一篇整理如下：

原文：机器人的位姿描述与坐标变换

一、刚体位姿

1. 刚体位姿：将描述刚体的3个位置自由度和3个方位即姿态自由度简称为刚体位姿。

2. 刚体位姿描述方法：

（1）建立坐标系

                                                    

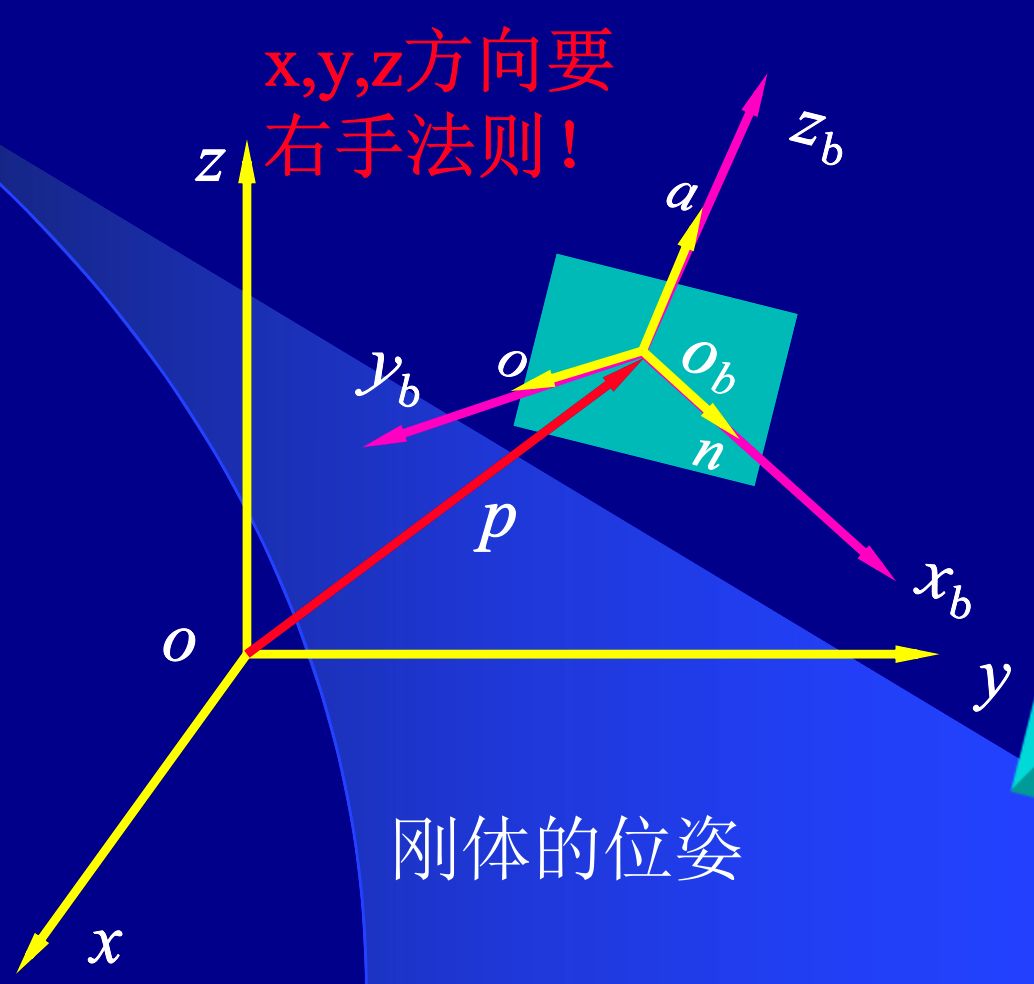
（2）位置描述

刚体的位置可以用一个3x1的矩阵来表示，即刚体坐标系原点Ob在基坐标系o-xyz中的位置。

刚体的位置描述为：

（3）姿态描述

用刚体坐标系的三个方向单位矢量n , o, a, 的方向余弦矩阵表示。

方向余弦矩阵书写为：

                                           

此方向余弦矩阵又称之为旋转矩阵。

（4）R正交性

由于旋转矩阵R的三个列向量n , o, a, 都是单位矢量，且双双相互垂直，因此旋转矩阵R的9个元素满足6个约束条件（正交条件）：

n.n=o.o=a.a=1

n.o=o.a=a.n=0

可见，旋转矩阵R是正交矩阵（Orthogonal Matrix），且R满足如下条件：

                                                                           

（5）刚体位姿描述

用4×4的齐次矩阵来表示刚体位姿，此矩阵称为刚体位姿矩阵。

                                                                               

 

二、机器人位姿描述

                                          

机器人手部的位姿可以用刚体位姿矩阵表示为：

                                                         

 

三、正交坐标变换

1. 正交坐标变换的一般形式

                                                         

点 p 在基础坐标系和刚体坐标系的位置矢量分别表示为：

                                                              

与之间的变换关系为：

                                              

从刚体坐标系到基础坐标系的一般变换关系式可以表示为：

                                                               

 

例题：如图所示，b坐标系原点与基础坐标系o-xyz的原点重合，x轴与xb轴之间的夹角为θz，另外，z轴与zb轴重合。

求：表示b系相对于基础坐标系o-xyz的位置矢量x0和旋转矩阵R，并求空间一点P=[u  v  w]T从b系到基础坐标系o-xyz的一般变换表达式。

                                                              

解：（1）位置矢量x0=0。

（2）求旋转矩阵R

                                                   

b系相对于基础坐标系o-xyz的旋转矩阵R为：

                                                               

（3）从b系到基础坐标系o-xyz的一般变换表达式为

                                                                    

                                                          

 

2. 绕坐标轴的旋转矩阵

（a）绕x轴旋转θ角的旋转矩阵

                                                            

                                                            

 

（b）绕y轴旋转θ角的旋转矩阵

                                                            

                                                            

 

（c）绕z轴旋转θ角的旋转矩阵

                                                             

                                                             

 

3. 绕任意轴的旋转矩阵

                       

 

4. 绕两个坐标轴旋转的变换矩阵

（1）相对动坐标系的变换顺序：

1）j系先绕着i系的z轴旋转θ角，得到m系；

2）绕新m系的x轴旋转α角，得到变换后的j系。

                                                                 

总的变换矩阵为：R=R(z,θ).R(x,α)

 

（2）相对定坐标系的变换

1）先绕参考坐标系i系的x轴旋转α角，得到n系；

2）再将n系绕参考z轴旋转θ角，得到j系。

                                                          

总的变换矩阵为：R=R(z,θ).R(x,α)

 

（3）总结：

坐标变换相对动系时，总变换矩阵中旋转矩阵相乘的顺序和变换顺序一致，变换矩阵右乘；

相对固定参考系时，总变换矩阵中旋转矩阵相乘的顺序和变换顺序相反，变换矩阵左乘。

 

5. 绕三个坐标轴旋转的变换矩阵

（1）基于欧拉角的欧拉变换

用欧拉角φ、θ、Ψ来规定一个转动序列所得到的变换。

欧拉变换顺序可以是：

于是可以得到：

                                                 

此时欧拉变换矩阵为：

                  

 

欧拉变换可以是Z-X-Z的顺序，也可以是其他的顺序，查阅wiki百科可以得到其他变换顺序的欧拉变换矩阵。

                            

 

当欧拉变换矩阵给定后，我们可以反向求解出欧拉角。

以Z-Y-Z变换顺序为例，此时欧拉变换矩阵为：

                                         

反求欧拉角可以得到：

                                    

 

（2）RPY变换

                               

横滚(Roll)：将船的行驶方向取为z轴，则绕z轴的旋转（α角）称横滚（回转）；

俯仰(Pitch)：把绕y轴的旋转(β角)称为俯仰(Pitch)；

偏转(Yaw)：而把铅直方向取为x轴，将绕x轴的旋转(γ角)称为偏转或侧摆(Yaw)。

 

RPY变换：将机器人操作臂手爪恣态用RPY角来表示，而手部与此相应的变换称为RPY变换。

 

RPY变换的旋转顺序：绕固定参考系的x轴回转γ角，再绕固定参考系的y轴转β角，最后绕固定参考系的z轴转α角。它们的总变换为：

          

 

通过RPY逆变换（即已知RPY变换矩阵），可以求解出RPY的三个旋转角γ、β和α。

                                         

得到   

 

四、齐次坐标变换

1. 齐次坐标

                  

                  

                                

 

2. 齐次变换（Homogeneous transform）

由平移和旋转组成的刚体运动的坐标变换一般关系式为：

                                                                          

用齐次坐标表示从坐标到基坐标的变换为：

                                                                 

简写为：

                                                                           

其中：

这个变换称之为齐次变换。

其中矩阵A称之为齐次变换矩阵。

 

3. 平移齐次变换

平移齐次变换矩阵可以表示为：

                                                                 

齐次平移变换为：

                                                                

例题：已知向量U=3i+4j+6k沿向量P=2i+5j-k平移，求：平移变换后生成的新向量V。

                                                          

解：若用矢量相加，可以得到：

V=U+P=(3+2)i+(4+5)j+(6-1)k=5i+9j+5k

若用齐次平移变换，可以得到：

                                                     

 

4. 旋转齐次变换

旋转齐次变换矩阵可以表示为：

                                                               

                                                               

                                                               

 

例题：已知齐次坐标系中一点U=[7，3，2，1]T，将此点绕Z轴旋转90度，再绕y旋转90度，求：旋转变换后所得的点W。

解：本题中是相对固定参考系的旋转，所以变换矩阵应该左乘。

                                                   

 

5. 平移加旋转的齐次变换

 

例题：空间某点的位置矢量为U=[a，b，c，1]T，它按如下顺序完成转动和移动：（1）绕z轴转动90°；（2）绕x转动90°；（3）沿着x, y, z 轴进行移动，[d，e，f]T。求：完成复合运动后的新位置矢量V。

解：本题中是相对固定参考系的旋转，所以变换矩阵应该左乘。

V= Trans(d, e, f)Rot(x, 90°)Rot(z, 90°)U

                                                      

 

五、坐标变换的相对性

这种坐标变换的实现是具有相对性的，可以相对于定坐标系，也可以相对于动坐标系。这种相对性具有普遍性。

（1）相对于定坐标系的变换实现

O2先绕基坐标绕的z轴旋转90度，相对基础坐标系平移(1,1,0)，最后得坐标系O2-x2y2z2。

                                                                      

相对于定坐标系

（2）相对于动坐标系的变换实现

O2先相对基坐标平移(1,1,0) ，再绕新坐标系的z轴旋转90度，最后得到坐标系O2-x2y2z2。

                                                                      

相对于动坐标系

 

六、坐标变换的逆变换

从坐标到基坐标的齐次变换为：

                                                                           

则其逆坐标变换为将基坐标系向量变换为刚体坐标系向量：

                                                                              

 

这需要求出齐次变换矩阵A的逆矩阵：

从刚体坐标系到基础坐标系的一般变换关系式可以重新表述为：

                                                       

由于旋转矩阵R是正交矩阵，所以

                                                                      

 于是可以得到：

                                                                

写成齐次变换的矩阵形式

                                                                 

于是得到齐次变换矩阵A的逆矩阵：

                                                                         

 

七、多坐标间的齐次变换及位姿变换方程

1. 多坐标系间的齐次变换

例题：如图所示，要求将空间一点P点从c系变换到b系，再将其由b系变换到基础参考系。求：其坐标变换。

                                                       

解：

                                                       

                                                       

 

多坐标系间变换公式的推广：

                                      

                                                             

我们称此式为齐次坐标变换方程式 。

总的变换矩阵为：

                                                             

 

2. 机器人的位姿变换方程

                                                          

建立机器人坐标系统，相应的变换矩阵有：

                                                       

工具坐标系E相对通用坐标系U的位姿，可以通过两种变换方法实现：

                                                            

                                                             

以上两式联立，

                                                          

于是，机械手H相对于基座B的位姿可以表示为：

                                                          

 

例题：一个棱柱体的原始位置如图所示，变换前定系和动系是重合的，棱柱体在动系中的位姿可用6个点的齐次坐标所组成的矩阵来描述为

                                                          

让棱柱体先绕Z轴转90°，再绕Y轴转90°，最后沿X方向平移4。

                                                           

求：变换后的棱柱体的位姿。

解：总变换矩阵为

                                                    

棱柱体上的六个点经变换后：

                                                          

变换后的棱柱体如下图所示

                                                             

至此，机器人的位姿描述和坐标变换内容介绍完毕。