机器人学：Matlab实现实时多次贝塞尔曲线(Bézier Polynomials)插值

本文结构0. 引言0.1 最终效果1. 贝塞尔插值1.1 Matlab代码实现1.2 测试代码0. 引言有时候对于三次、五次实时插值并不满足我们的控制需求，而贝塞尔曲线插值越来越受到关注。0.1 最终效果1. 贝塞尔插值对于一维M次贝塞尔曲线的公式为：b(s)=∑k=0MαkM!k!(M−k)!sk(1−s)M−kb(s) = \sum\limits_{k = 0}^M {{\alpha _k}}

陶技者

2736人浏览 · 2020-05-25 21:28:20

陶技者 · 2020-05-25 21:28:20 发布

0. 引言

有时候对于三次、五次实时插值并不满足我们的控制需求，而贝塞尔曲线插值越来越受到关注。

0.1 最终效果

下图是一个七次插值的贝塞尔曲线形状
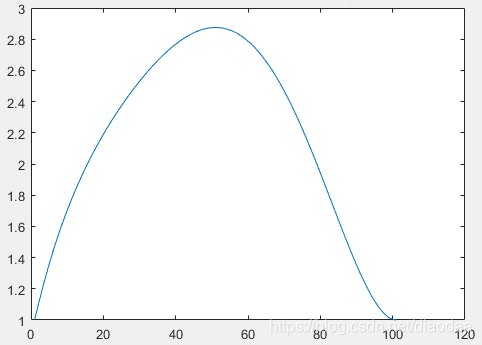
在这里插入图片描述

1. 贝塞尔插值

对于一维M次贝塞尔曲线的公式为：
$\sum\limits_{k = 0}^M {{\alpha _k}} \frac{{M!}}{{k!(M - k)!}}{s^k}{(1 - s)^{M - k}}$

例如，对于 $M = 5$ 的贝塞尔曲线， $\alpha$ 与 $s$ 的关系如下图：
在这里插入图片描述
通过这个例子，你就可以理解贝塞尔的变量关系，从而设置满足自己要求的曲线参数。
其他贝塞尔曲线性质可以这样描述：

更多动态展示你可以查看这里的视频；

1.1 Matlab代码实现

function [res] = bezierPolynomials(s,alpha)
% s在[0,1]之间 alpha决定着曲线的形状
    M = size(alpha,2)-1;% 只需要设定alpha的大小M就确定了
    M_factorial = factorial(M);
    res = 0;
    for k = 0:1:M
       res = res + M_factorial/(factorial(k)*factorial(M-k))*alpha(k+1)*s^k*(1-s)^(M-k);
    end
end

1.2 测试代码

clear
clc

alp = [0.1 0.3 0.2 0.5 0.1 0.1]*10;

s = [0:0.01:1];
dat = [];
for i = 1:size(s,2)
    dat = [dat;bezierPolynomials(s(i),alp)];
end
plot(dat);

效果就是上图所示，可以通过参数优化设计属于自己的曲线类型。