【编译原理-练习题-2】词法分析大题
题型1:正规表达式构造NFA
1.构造正规表达式a(aa)*bb(bb)*a(aa)* 的NFA(非确定有限自动机)。
解

2.对正规式(a|b)*abb构造其等价的NFA。
解

3.构造正规表达式((a|b)*|aa)*b的NFA。
解:

题型二:NFA转换为DFA
4.设M=( {x,y}, {a,b}, f, x, {y} )为一NFA(非确定的有限自动机),其中f定义如下:
f(x,a)={x,y} f{x,b}={y}
f(y,a)=Φ f{y,b}={x,y}
试构造相应的确定有限自动机M′。
解:
1)对照确定有限自动机的定义M=(S,Σ,f,So,Z),
- S是一个有限状态集,他的每一个元素称为状态
- Σ是一个又穷输入字母表他的每一个元素称为一个输入字符
- f是一个从S*Σ到S的单值映射,即f(si,a)=sj,且有si,sj属于S和a属于Σ
- S0是初态
- Z是终态集
由f的定义可知f(x,a)、f(y,b)均为多值函数,不满足定义,因此M是一非确定有限自动机。
2)先画出NFA M相应的状态图,如下图所示。
由M=( {x,y}, {a,b}, f, x, {y} )可知初态是x,终态是y
f(x,a)={x,y} ---------- 表示x接收a字符到x,y
f{x,b}={y} ---------- 表示x接收b字符到y
f(y,a)=Φ ---------- 表示y接收a字符到空
f{y,b}={x,y} ---------- 表示y接收b字符到x,y
3)用子集法构造状态转换矩阵,如下表所示。
4)将转换矩阵中的所有子集重新命名,形成下表所示的状态转换矩阵,即得到
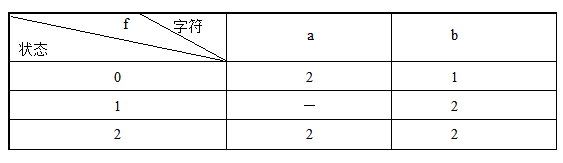
5)M′=({0,1,2},{a,b},f,0,{1,2}),M′状态转换图如下图所示。
5.将下图所示的非确定有限自动机(NFA)变换成等价的确定有限自动机(DFA)。其中,X为初态,Y为终态。

解
用子集法将NFA确定化,如图所示。

确定化的DFA如下图所示: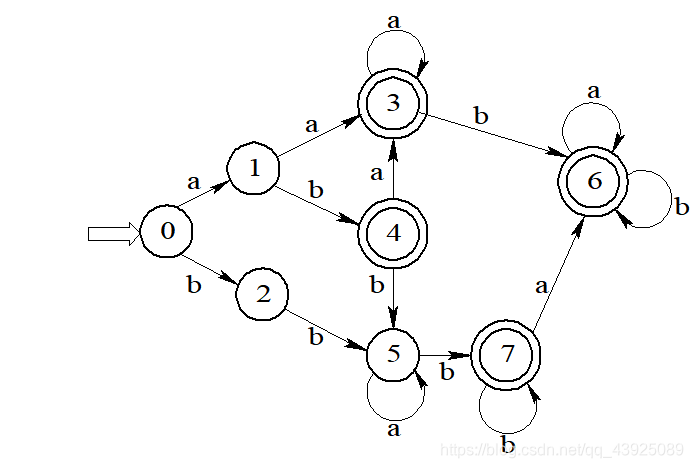
题型三:DFA最小化
6.将以下DFA(确定有限自动机) 最小化

解:
1)将状态分解为
- 终态集{Y}
- 非终态集{X,1,2}
2)考察非终态集{X,1,2}接收a字符
- X接收a字符到1 (1属于非终态集)
- 1不接收字符
- 2接收a字符到1 (1属于非终态集)
故将非终态集{X,1,2},分为{X,2},{1}
3)考察{X,2}接收b字符
- X接收不接受b
- 2接收不接受b
4)按顺序重新命名状态子集{X,2},{1},{Y}为0,1,2得到状态转换矩阵
| S | a | b |
|---|---|---|
| 0 | 1 | 空 |
| 1 | 空 | 0 |
| 2 |
5)根据状态转换矩阵绘制化简后的状态转换图
7.将下图所示的确定有限自动机(DFA)最小化。其中,X为初态,Y为终态。
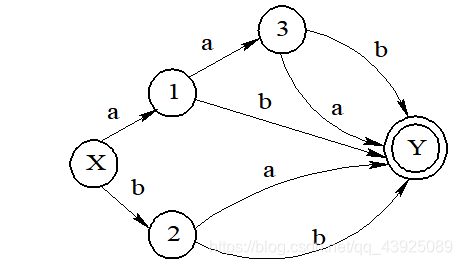
解
先划分为终态集{Y}和非终态集I={X,1,2,3}
X面对输入符号b时下一状态属于I,而1,2,3面对输入符号b时下一状态属于{Y},故划分为{X}、{1,2,3}
非终态2和非终态3面对输入符号a的下一状态相同,而1不同,即最简状态{X}、{1}、{2,3}、{Y}。按顺序重新命名为0、1、2、3,则得到最简DFA,
8.将下图的DFA最小化。

解
初始划分:II={{0,1,2},{3,4}}(1分)
(1)考查{0,1,2},1和2接受a,b后都转向相同的状态,且接受b后转向终态,而0接受b后转向非终态2,所以0与1,2可分,IInew={{0},{1,2},{3,4}}(1分)
(2)考查{3,4},接受a,b后都转向相同的状态,所以3,4不可分。IInew={{0},{1,2},{3,4}}(1分)
将1,2合并用1代表,3,4合并用3代表,最终的最小化DFA如下:
| I | a | b |
|---|---|---|
| 0 | 1 | 2 |
| 1 | 1 | 2 |
| 2 | 2 | 2 |

题型四:正规表达式求DFA
9.构造正规表达式a(aa)*bb(bb)*a 的最小化的确定有限自动机M′。
解:
先画出正规式相应的NFA M状态图,如下图所示。
用子集法构造状态转换矩阵,如下表所示。
观察状态转换矩阵,发现I中含有Y的为终态集,则:
将状态分为终态集{Y}和非终态集{X,1,2,3,4,5}
非终态集{X,1,2,3,4,5}
X接收a字符到1 1属于非终态集
1接收a字符到2 2属于非终态集
2接收a字符到1 1属于非终态集
3接收a字符到-
4接收a字符到Y
5接收a字符到-
所以非终态集分为{X,1,2},{3,5},{4}
X接收b字符到-
1接收b字符到3
2接收b字符到-
因为{X,1,2}b={,3,},所以分为{X,2},{1},
3接收b字符到4
5接收b字符到4
最后得到集合{X,2},{1},{3,5},{4},{Y}重新命名为1,2,3,4,5得到最小化的DFA M′状态转换矩阵和状态转换图如下图所示。

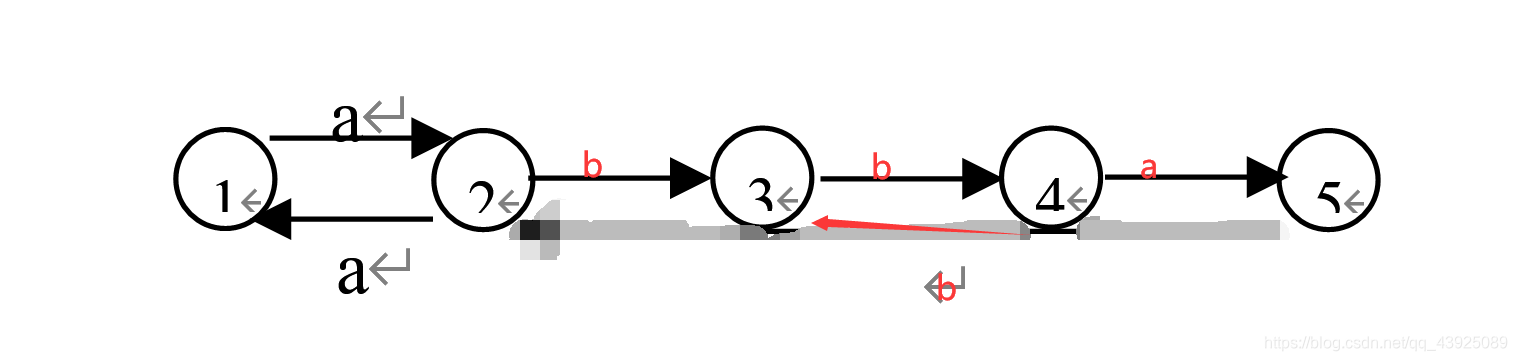
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容






















所有评论(0)