数据挖掘课程作业代码实现

一、课后习题2.41、求均值、中位数和标准差age = [23, 23, 27, 27, 39, 41, 47, 49, 50, 52, 54, 54, 56, 57, 58, 58, 60, 61]fat = [9.5, 26.5, 7.8, 17.8, 31.4, 25.9, 27.4, 27.2, 31.2, 34.6, 42.5, 28.8, 33.4, 30.2, 34.1, 3...

程勇uestc

2940人浏览 · 2020-03-25 09:22:00

程勇uestc · 2020-03-25 09:22:00 发布

一、课后习题2.4

在这里插入图片描述

1、求均值、中位数和标准差

age = [23, 23, 27, 27, 39, 41, 47, 49, 50, 52, 54, 54, 56, 57, 58, 58, 60, 61]
fat = [9.5, 26.5, 7.8, 17.8, 31.4, 25.9, 27.4, 27.2, 31.2, 34.6, 42.5, 28.8, 33.4, 30.2, 34.1, 32.9, 41.2, 35.7]

def mean(List):
    """计算列表List的均值并返回"""
    return sum(List) / len(List)

def medium(List):
    """计算列表List的中位数"""
    List = sorted(List)
    n = len(List)
    mid = int(n / 2)
    if(n % 2 == 0):  # 列表长度为偶数
        return (List[mid - 1] + List[mid]) / 2
    return List[mid]

def std(List):
    """计算列表的标准差"""
    n = len(List)
    men = mean(List)
    sum = 0
    for i in range(n):
        sum += (List[i] - men)**2
    ret = (sum / (n - 1))**0.5
    return ret

if __name__ == '__main__':
    print("age的均值为: {}, 中位数为: {}, 标准差为: {}".format(mean(age), medium(age), std(age)))
    print("fat的均值为: {}, 中位数为: {}, 标准差为: {}".format(mean(fat), medium(fat), std(fat)))

$\quad$ 程序运行结果如下：
在这里插入图片描述

2、绘制盒图

$\quad$ 盒图的形式如下：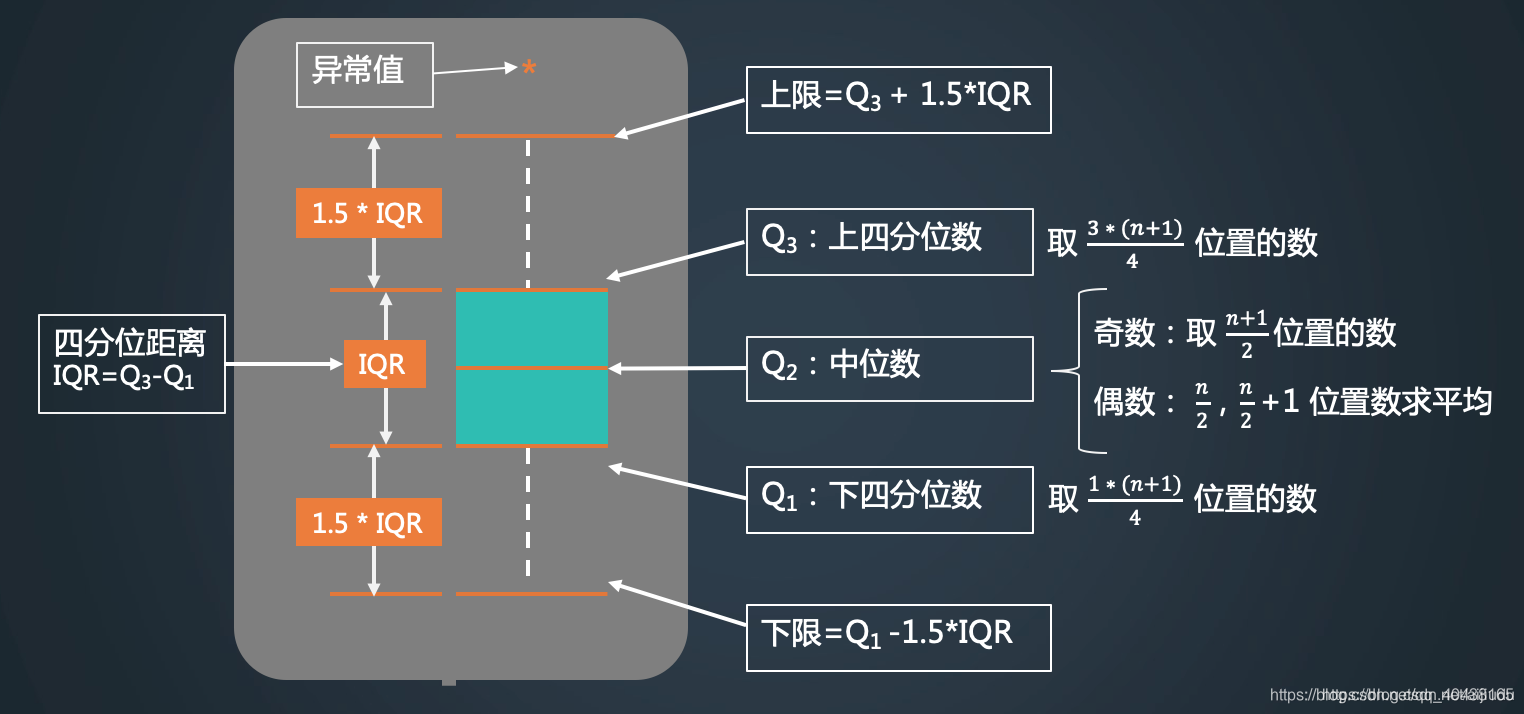
在这里插入图片描述
$\quad$ 在python的pandas库中，我们可以直接得到数据的统计信息，也可以直接画出盒图，程序如下：

import pandas as pd
import matplotlib.pyplot as plt

age = [23, 23, 27, 27, 39, 41, 47, 49, 50, 52, 54, 54, 56, 57, 58, 58, 60, 61]
fat = [9.5, 26.5, 7.8, 17.8, 31.4, 25.9, 27.4, 27.2, 31.2, 34.6, 42.5, 28.8, 33.4, 30.2, 34.1, 32.9, 41.2, 35.7]

def boxPlot(List, title):
    """绘制列表List的盒图"""
    df = pd.DataFrame(List)
    df.plot.box(title=title)  # 绘制盒图名称
    plt.grid(linestyle="--", alpha=0.3)
    plt.show()

if __name__ == '__main__':
    print(pd.DataFrame(age).describe())  # 对数据的各个属性进行描述
    boxPlot(age, title="age")
    print(pd.DataFrame(fat).describe())  # 对数据的各个属性进行描述
    boxPlot(fat, title="fat")

age的描述为：

count  18.000000  数据数目
mean   46.444444  均值
std    13.218624  方差
min    23.000000  最小值
25%    39.500000  下四分位数Q1
50%    51.000000  中位数
75%    56.750000  上四分位数Q3
max    61.000000  最大值

fat描述为

count  18.000000
mean   28.783333
std     9.254395
min     7.800000
25%    26.675000
50%    30.700000
75%    33.925000
max    42.500000

age的盒图为：
fat的盒图为：

3、绘制这两个变量的散点图和q-q图

$\quad$ python上绘制q-q图不是很方便，可在matlab中完成

age = [23 23 27 27 39 41 47 49 50 52 54 54 56 57 58 58 60 61];
fat = [9.5 26.5 7.8 17.8 31.4 25.9 27.4 27.2 31.2 34.6 42.5 28.8 33.4 30.2 34.1 32.9 41.2 35.7];
qqplot(age, fat);
title('q-q图');

二、课后习题2.8

在这里插入图片描述

target = [1.4, 1.6]  # 查询点
# data存放x1到x5五个点的信息，x1 = [1.5, 1.7, 0]表示x1坐标为(1.5, 1.7)，距离查询点距离为0
data = [[1.5, 1.7, 0], [2, 1.9, 0], [1.6, 1.8, 0], [1.2, 1.5, 0], [1.5, 1.0, 0]]

def Euclid(A, B):
    """计算A和B的欧式距离"""
    n = min(len(A), len(B))
    ret = 0
    for i in range(n):
        ret += (A[i] - B[i])**2
    return ret**0.5

def Manhattan(A, B):
    """计算A和B的曼哈顿距离"""
    n = min(len(A), len(B))
    ret = 0
    for i in range(n):
        ret += abs(A[i] - B[i])
    return ret

def Supremum(A, B):
    """计算A和B的上确界距离"""
    n = min(len(A), len(B))
    ret = 0
    for i in range(n):
        ret = max(ret, abs(A[i] - B[i]))
    return ret

def Cosine(A, B):
    """计算A和B的余弦距离"""
    n = min(len(A), len(B))
    up = 0
    for i in range(n):
        up += A[i] * B[i]
    normA, normB = 0, 0
    for i in range(n):
        normA += A[i]**2
        normB += B[i]**2
    normA, normB = normA**0.5, normB**0.5
    return up / (normA * normB)

def solve(method):
    n = len(data)
    for i in range(n):
        data[i][2] = method(data[i][:2], target)  # 用传入的method的方法计算距离
    ret = sorted(data, key=lambda item: item[2])  # 按照距离从小到大排序
    print(method.__name__, ret)
    
if __name__ == '__main__':
    methods = [Euclid, Manhattan, Supremum, Cosine]
    for method in methods:
        solve(method)

$\quad$ 输出结果如下，每一行表示在该距离衡量方法下查询点到 $x_1,\cdots,x_5$ 这5个点距离从小到大的排序值。例如Euclid方法下表示查询点距离点(1.5,1.7)距离最小，距离是1.414。

Euclid [[1.5, 1.7, 0.14142135623730948], [1.2, 1.5, 0.22360679774997896], [1.6, 1.8, 0.28284271247461906], [1.5, 1.0, 0.608276253029822], [2, 1.9, 0.6708203932499369]]
Manhattan [[1.5, 1.7, 0.19999999999999996], [1.2, 1.5, 0.30000000000000004], [1.6, 1.8, 0.40000000000000013], [1.5, 1.0, 0.7000000000000002], [2, 1.9, 0.8999999999999999]]
Supremum [[1.5, 1.7, 0.10000000000000009], [1.2, 1.5, 0.19999999999999996], [1.6, 1.8, 0.20000000000000018], [2, 1.9, 0.6000000000000001], [1.5, 1.0, 0.6000000000000001]]
Cosine [[1.5, 1.0, 0.9653633930282662], [2, 1.9, 0.9957522612528874], [1.2, 1.5, 0.9990282349375618], [1.6, 1.8, 0.9999694838187877], [1.5, 1.7, 0.999991391443956]]

$\quad$ 对于第二问，将数据规范化后再计算查询点与这五个点的欧氏距离，程序如下：

target = [1.4, 1.6]  # 查询点
# data存放x1到x5五个点的信息，x1 = [1.5, 1.7, 0]表示x1坐标为(1.5, 1.7)，距离查询点距离为0
data = [[1.5, 1.7, 0], [2, 1.9, 0], [1.6, 1.8, 0], [1.2, 1.5, 0], [1.5, 1.0, 0]]
def normlize(List):
    """规范化数据，使得List的范数为1"""
    l2 = (List[0]**2 + List[1]**2)**0.5
    List[0] /= l2
    List[1] /= l2
    return List
def Euclid(A, B):
    """计算A和B的欧式距离"""
    n = min(len(A), len(B))
    ret = 0
    for i in range(n):
        ret += (A[i] - B[i])**2
    return ret**0.5
def solve():
    """将数据规范化后计算距离并排序"""
    n = len(data)
    for i in range(n):
        data[i][:2] = normlize(data[i][:2])
        data[i][2] = Euclid(data[i][:2], normlize(target))  # 用传入的method的方法计算距离
    ret = sorted(data, key=lambda item: item[2])  # 按照距离从小到大排序
    print(method.__name__, ret)
    
if __name__ == '__main__':
    solve()

$\quad$ 结果如下：

Euclid [[0.6616216370868464, 0.7498378553650925, 0.004149350803200864], [0.6643638388299198, 0.7474093186836597, 0.007812321193114019], [0.6246950475544242, 0.7808688094430303, 0.044085486555962686], [0.7249994335944139, 0.6887494619146931, 0.09217091457843411], [0.8320502943378437, 0.5547001962252291, 0.2631980507972417]]

课后习题3.3

在这里插入图片描述

$\quad$ 这里给出第一问平滑的程序：

def smooth(data, k):
    """k为光滑箱深度，data为需平滑的数据，这里我们假设data长度能整除k"""
    ret = []
    n = len(data) // k
    for i in range(n):
        sum = 0
        for j in range(i*k, (i+1)*k):
            sum += data[j]
        avg = sum / k
        for j in range(k):
            ret.append(avg)
    return ret

if __name__ == '__main__':
    age = [13, 15, 16, 16, 19, 20, 20, 21, 22, 22,
           25, 25, 25, 25, 30, 33, 33, 35, 35, 35,
           35, 36, 40, 45, 46, 52, 70]
    age = smooth(age, k=3)
    print(age)

$\quad$ 运行结果：

[14.666666666666666, 14.666666666666666, 14.666666666666666, 18.333333333333332, 18.333333333333332, 18.333333333333332, 21.0, 21.0, 21.0, 24.0, 24.0, 24.0, 26.666666666666668, 26.666666666666668, 26.666666666666668, 33.666666666666664, 33.666666666666664, 33.666666666666664, 35.0, 35.0, 35.0, 40.333333333333336, 40.333333333333336, 40.333333333333336, 56.0, 56.0, 56.0]

课后习题3.7

$\quad$ 给出程序如下：

import numpy as np

def minmaxScaler(data, target):
    """将数据规范化到[0, 1]区间"""
    Min, Max = data[0], data[0]
    n = len(data)
    for i in range(n):
        Min = min(Min, data[i])
        Max = max(Max, data[i])
    target = (target - Min) / (Max - Min)
    return target

def zScaler(data, target):
    """将data进行z-score规范化"""
    Mean, std = np.mean(data), np.std(data)
    target = (target - Mean) / std
    return target

def pivotScaler(data, target):
    """将data使用小数定标规范化"""
    Max = np.max(data)
    j = len(str(Max))
    return target / (10**j)

if __name__ == '__main__':
    age = [13, 15, 16, 16, 19, 20, 20, 21, 22, 22,
           25, 25, 25, 25, 30, 33, 33, 35, 35, 35,
           35, 36, 40, 45, 46, 52, 70]

    print(minmaxScaler.__name__, minmaxScaler(age, 35))
    print(zScaler.__name__, zScaler(age, 35))
    print(pivotScaler.__name__, pivotScaler(age, 35))

$\quad$ 结果如下：

minmaxScaler 0.38596491228070173
zScaler 0.3966110348537352
pivotScaler 0.35

课后习题3.12

在这里插入图片描述

点击阅读全文

永洪数据分析社区

永洪科技，致力于打造全球领先的数据技术厂商，具备从数据应用方案咨询、BI、AIGC智能分析、数字孪生、数据资产、数据治理、数据实施的端到端大数据价值服务能力。

更多推荐

【2025年泰迪杯数据挖掘挑战赛】B题详细解题思路+数据预处理+代码分享

初步分析整理了B题的赛题分析与解题思路，后面还会更新详细的建模论文与解题代码，明天完成！

永洪数据分析社区

2025年泰迪杯数据挖掘竞赛B题论文首发+问题一二三四代码分享

针对问题二，将处理后的数据集，进行合并为一个完整的数据集作为训练数据集，性别（Sex）和年龄（Age）为类别变量，加速度计数据作为输入数据，MET值作为输出数据，引入随机森林回归器、随机森林、支持向量机、多层感知机、GBDT进行训练模型，并利用RMSE对模型精度进行评估。原始数据存储于CSV格式文件中，其中记录了时间戳和对应的三轴加速度值（X，Y，Z轴），这些数据反映了个体在空间中各个方向上的加