完整内容预计36h更新完毕,获取请看文末简介使用传统优化方法（如Gurobi或CPLEX）来构建和求解经典的单元调度（UC）模型。定义变量：目标函数：目标是最小化总的运行成本，包括燃料成本和启停成本：[\text{Objective} = \sum_{t=1}^{T} \sum_{i=1}^{N} \left( C_f(p_{i,t}) + C_{s,i}(x_{i,t-1}, x_{i,t})

通过建立三维坐标系，并结合运动学原理和向量计算，我们可以有效地计算机器人左手末端的最终位置。通过分析各关节的角度和位置变化，并验证其是否符合安全要求，确保机器人能够安全、顺畅地完成该动作。通过运动学建模和S-curve模型，求解了机器人在从起始点到目标点之间的路径和时间规划，并通过分析膝关节的加速度变化来找出最大角度变化时刻。通过建立协同运动模型，利用圆周运动和逆向动力学分析，确保机器人在执行复杂

完整文章以及1-4问代码结果已更新完毕,获取请看文末简介摘要在问题一中，旨在研究PDMS薄膜在不同厚度和折射率条件下的辐射率随波长变化的规律，进而分析其在辐射冷却技术中的应用潜力。通过建立数学模型，首先计算了薄膜的反射率和透过率，并据此推导出其发射率，进而评估其辐射冷却能力。为了优化薄膜的冷却性能，我们采用了优化算法，最大化辐射冷却功率，确定最优的薄膜厚度和折射率组合。最终，结果表明薄膜的发射率随

PDMS薄膜的发射率（(\epsilon(\lambda, d))）是材料在特定波长和厚度下的辐射能力。我们需要建立一个模型，描述不同波长（(\lambda)）和不同薄膜厚度（(d)）下的发射率。

评估指标体系 - 任务1（二分类）：准确率、召回率、F1值、AUC；识别并定位图像中的破损区域，明确其类型（裂纹、凹陷、穿孔、锈蚀等），并在每张图像中输出最多四个按严重程度排序的破损区域。通过对集装箱表面图像的智能分析与识别，可以快速判断其是否存在损伤、损伤类型及程度，从而为后续维修与流转提供决策依据。对策：采用模型蒸馏与轻量化网络（RT-DETR-S、YOLOv8-n）。1.数据检查与分析：标注

因此，如何科学评估客户索赔的合理性、预测赔付金额、识别高风险索赔案件，是智能风控体系中的核心课题。1.问题1（规则生成）：以数据分布为依据，构建“合理诉求—诉求偏高—严重超额”的分级规则，保证阈值随赔付金额单调上升，符合业务逻辑；3.问题3（分类识别）：利用问题1标注的标签训练分类模型，实现风险预测，并探讨直接分类与“回归+规则判类”两种路径的优劣。附件1（训练集）：包含已结案的历史运单数据，其

然而，残差分析揭示，随着预测金额的增加，模型在高赔付金额区域的误差逐渐放大，提示未来需要进一步优化模型以处理特殊情况。接着，使用80%和97%分位数作为合理诉求与诉求偏高、诉求偏高与严重超额的边界，并通过保序回归平滑分位数边界，确保随着赔付金额的增加，风险分类的阈值逐渐上升。1.方法合理，贴合业务逻辑.本文在风险标注环节引入分位数回归与保序回归相结合的策略，不仅保障了风险阈值的单调性，还充分考虑了

处理样本音频，要求在论文中 给出每个音频包含的噪声种类，去噪后的音频文件的信噪比，并分析 在不同噪声类型和强度下的适用范围与局限性。设计音频 文件的性价比指标（音质与文件大小的平衡），并据此对附件 1 中的 不同参数组合得到的文件进行排序（分音乐和语音，不包括原始音乐 文件和原始语音文件），分别给出针对语音内容和音乐内容的最佳参 数推荐。在工程实践中，我们会使用不同的编码算法（如MP3的有损压缩、

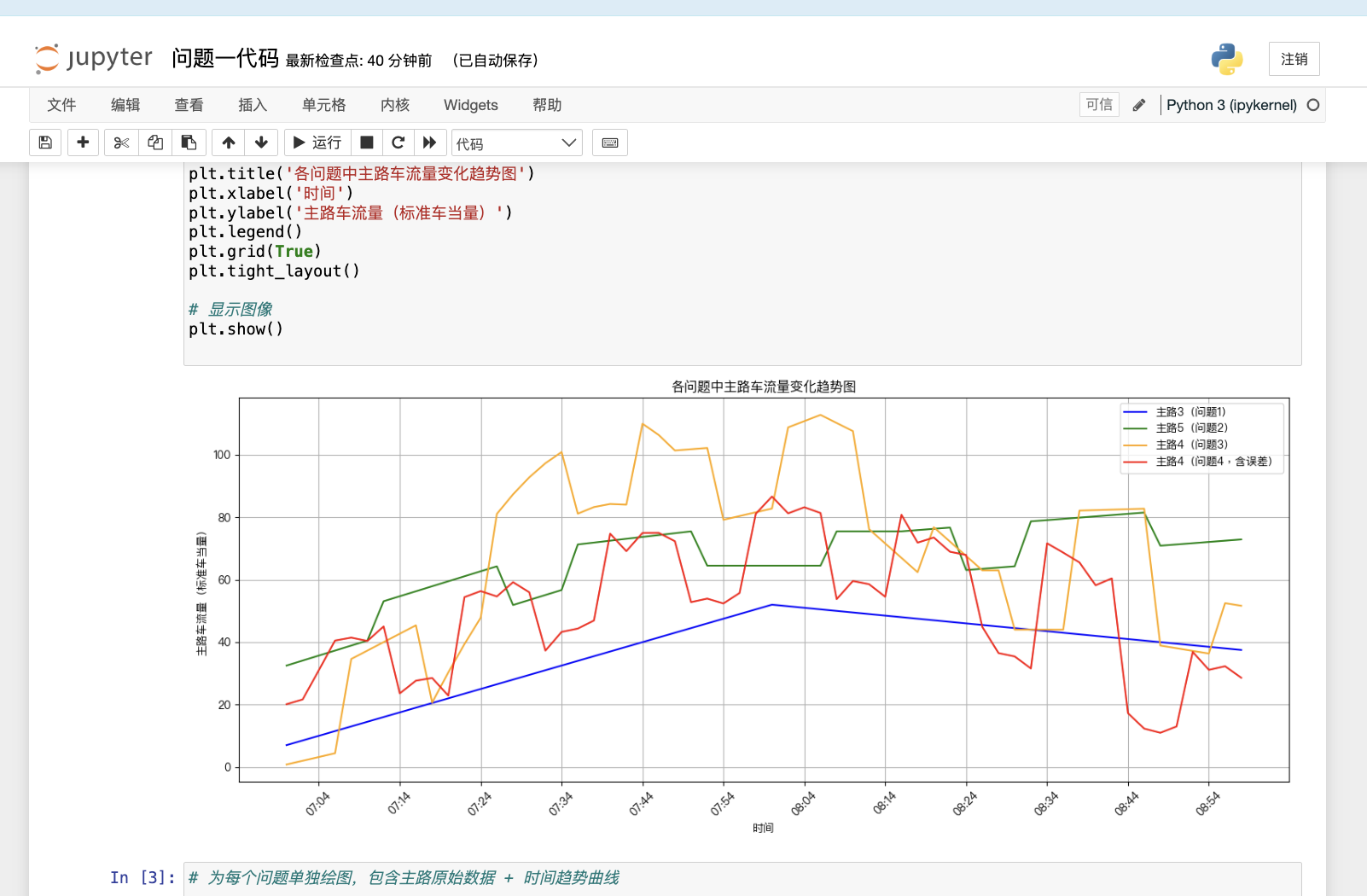
f3(t)={0,tmod  18∈[0,8) (红灯)g(t),tmod  18∈[8,18) (绿灯，g可为常数/线性)主路车流量 F(t)=f1(t)+f2(t)，用最小二乘拟合主路数据得到未知参数；推测4个支路的函数表达式（支路4为周期函数），并给出7:30、8:30时刻的车流值。问题3中需覆盖所有灯控状态变化点，如 7:06, 7:16, 7:24…套用延时关系后：F(t)=f1(t−1

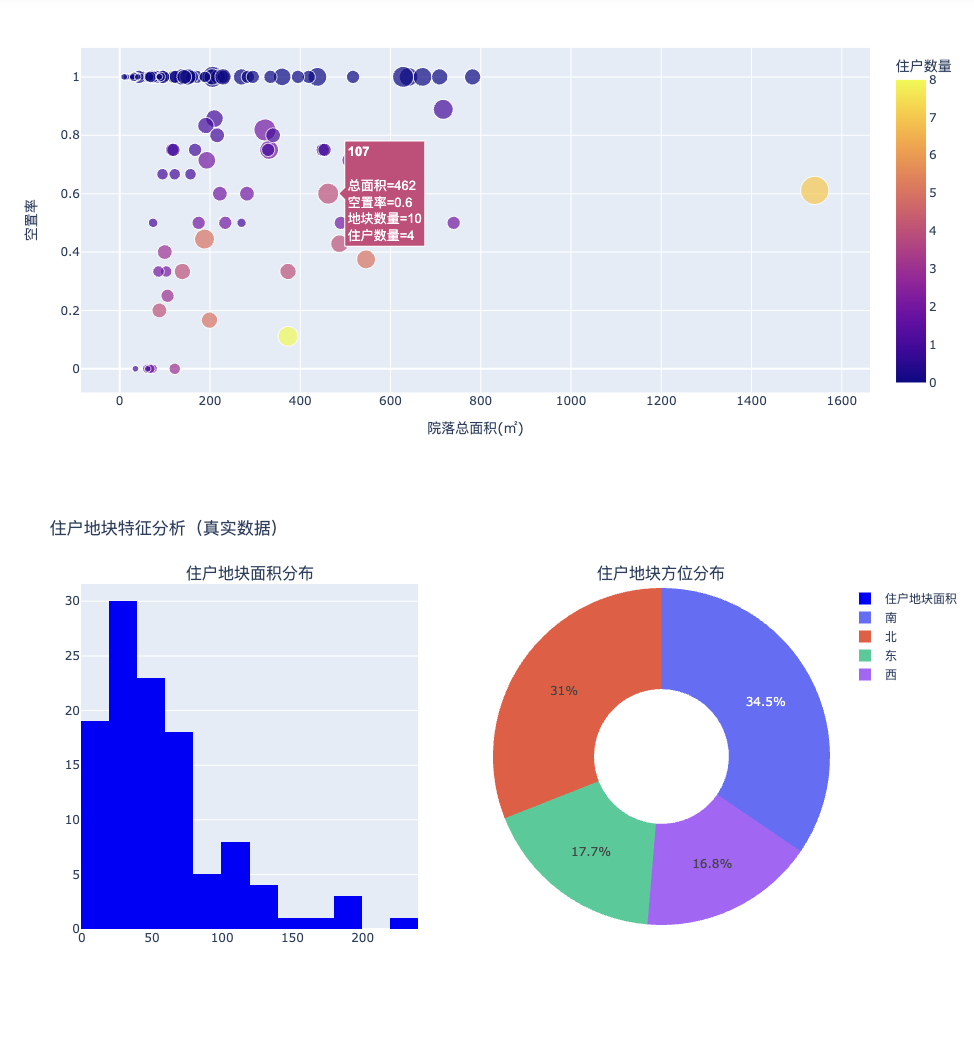
我们从三个维度建立补偿模型：面积补偿确保居民居住空间不缩减，设定迁入地块面积下限为原面积，上限为原面积的130%，既保证基本需求又控制开发商成本。首先将院落按潜在腾空面积排序，优先处理能腾空大面积院落的搬迁组合。约束条件包括：面积补偿约束(1≤A_k/A_j≤1.3)、采光约束(O_k≥O_j)、总成本约束(∑C_ijk≤2600万)，以及每户最多搬迁一次的完整性约束。定义性价比m=(ΔR×10)