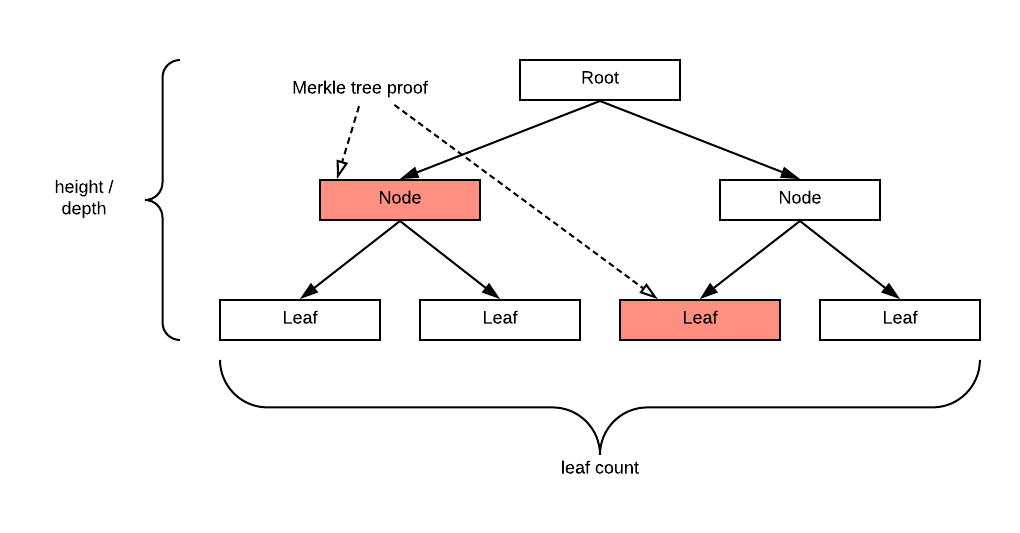
一个区块中的交易总数是一个重要的信息。我们展示了如何在没有受信任的第三方的情况下获得它，这在以前被认为是不可能的。范围让我们将 Merkle 路径的长度表示为 n。叶子的数量，即一个区块中的交易数量，介于 2^(n-1) + 1 和 2^n 之间。这是因为高度为 n 的满二叉树¹ 恰好有 2^n 个叶子。Merkle 路径的长度与 Merkle 树的高度相同。高度 2 的满二叉树确切数字查找最后一

区块头包含区块创建时的时间戳。但通常我们想要访问块高度，它不包含在块头中。我们设计了一种新技术来无需信任地获取包含在 coinbase 交易中的块高度。Coinbase 交易的区块高度coinbase 交易是区块中的第一笔交易。区块中的 Coinbase 交易BIP34 规定区块高度必须是 coinbase 交易解锁脚本中的第一项，如下所示。一个Coinbase 交易函数 blockHeight(

我们已经演示了在 BSV 上运行一个成熟的深度神经网络，其中机器学习 (ML) 算法的输入和模型都是公开的。在实践中，通常希望将输入或模型保持在链下并因此保持私有，同时仍确保 ML 算法如实运行。我们通过将零知识证明 (ZKP) 应用于 ML 来实现这一点。

比特币原生脚本是一种低级语言，是比特币虚拟机的操作码集合。通常情况下，比特币智能合约开发者不必直接处理它，可以使用 sCrypt 等高级语言。 但是，在某些情况下可能需要直接使用原生脚本。例如，自定义的脚本经过优化，可能比 sCrypt 生成的脚本更高效；又或者脚本是使用 MiniForth 等外部工具生成的，需要集成到 sCrypt 中。内联脚本函数我们在 sCrypt IDE 0.4.0 中引

当谈及智能合约时，大多数人都会下意识地把 Bitcoin 排除范围之外，因为当下流行的观点是 Bitcoin 不具有智能合约的能力。但是今天想跟大家介绍的内容则正好与此相反：即 Bitcoin 从诞生之日即拥有支持智能合约的能力，下面让我们一起来探个究竟。

今天可以在 BSV 上开发信息不完整的游戏，因为我们已经在其上实现了 zk-SNARKs。由于 BSV 上的智能合约交易便宜且即时，因此它是构建此类游戏的理想平台。