
简介
该用户还未填写简介
擅长的技术栈
未填写擅长的技术栈
可提供的服务
暂无可提供的服务
入门:The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices辅助阅读+总结
假设给定的数据被排列为大矩阵 D ∈ Rm×n 的列。估计低维子空间的数学模型是找到一个低秩矩阵A,使得A和D之间的差异最小化,从而导致以下约束优化:其中 r ≪ min(m, n) 是子空间的目标维度, ‖ · ‖F 是 Frobenius 范数,其对应于假设数据被 i.i.d的 高斯噪声损坏。这个问题可以通过先计算 D 的奇异值分解(SVD),然后将 D 的列向量投影到 D 的 r 个主左奇异
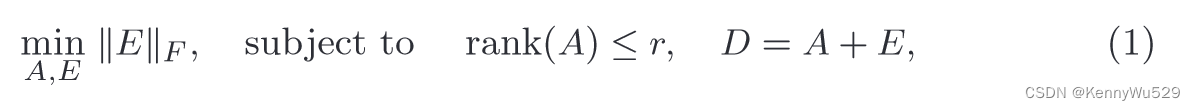
到底了










