控制论大题速成| 02 时域分析
初值定理limt→+∞f(t)=lims→0sF(s)\lim_{t\to +\infty}f(t)=\lim_{s\to 0}sF(s)t→+∞limf(t)=s→0limsF(s)终值定理limt→0+f(t)=lims→+∞sF(s)\lim_{t\to 0^+}f(t)=\lim_{s\to +\infty}sF(s)t→0+limf(t)=s→+∞limsF(s)y(t)
控制论大题速成| 02 时域分析
lalplace的性质
- 简单laplce变化对儿
| 原函数 | 像函数 |
|---|---|
| t n t^n tn | n ! s n + 1 \frac{n!}{s^{n+1}} sn+1n! |
| sin ω t \sin \omega t sinωt | ω s 2 + ω 2 \frac{\omega}{s^{2}+\omega^2} s2+ω2ω |
| cos ω t \cos \omega t cosωt | s s 2 + ω 2 \frac{s}{s^{2}+\omega^2} s2+ω2s |
| e − a t f ( t ) e^{-at}f(t) e−atf(t) | F ( s + a ) F(s+a) F(s+a) |
| f ( t − τ ) f(t-\tau) f(t−τ) | e − τ s F ( s ) e^{-\tau s}F(s) e−τsF(s) |
- Laplace性质
初值定理
lim t → + ∞ f ( t ) = lim s → 0 s F ( s ) \lim_{t\to +\infty}f(t)=\lim_{s\to 0}sF(s) t→+∞limf(t)=s→0limsF(s)
终值定理
lim t → 0 + f ( t ) = lim s → + ∞ s F ( s ) \lim_{t\to 0^+}f(t)=\lim_{s\to +\infty}sF(s) t→0+limf(t)=s→+∞limsF(s)
基础知识
y ( t ) = ∑ i = 1 n A 1 i e s i t + ∑ i = 1 n A 2 i e s i t ⏞ 自由响应 + B ( t ) ⏞ 强迫响应 y(t) = \overbrace{\sum_{i=1}^{n} A_{1i} e^{s_i t} + \sum_{i=1}^{n} A_{2i} e^{s_i t}}^{\text{自由响应}} + \overbrace{B(t)}^{\text{强迫响应}} y(t)=i=1∑nA1iesit+i=1∑nA2iesit
自由响应+B(t)
强迫响应
∑ i = 1 n A 1 i e s i t ⏟ 零输入响应 + ∑ i = 1 n A 2 i e s i t + B ( t ) ⏟ 零状态响应 \quad\quad\quad\underbrace{\sum_{i=1}^{n} A_{1i} e^{s_i t}}_{\text{零输入响应}} + \underbrace{\sum_{i=1}^{n} A_{2i} e^{s_i t} + B(t)}_{\text{零状态响应}} 零输入响应
i=1∑nA1iesit+零状态响应
i=1∑nA2iesit+B(t)
系统的固有特性由阶次 n n n和特征根 s i s_i si决定,其稳定的充要条件是所有的特征根实部为负数。特征根对自由响应的影响:
- 特征根的实部影响自由响应项的收敛性
- 若所有特征根均具有负实部,则系统自由响应收敛(系统稳定)
- 若存在特征根的实部为正,则系统自由响应发散(系统不稳定)
- 若存在特征根的实部为零,其余实部为负,则系统的自由响应等幅振荡(系统临界稳定)
- 特征根的虚部影响自由响应项的振荡性
虚部绝对值越大,自由响应项的振荡越剧烈。
示例
一阶系统的时域分析
X i ( s ) = 1 s X_i(s)=\frac{1}{s} Xi(s)=s1
那么就有:
x o ( t ) = L − 1 [ 1 T s + 1 1 s ] = L − 1 [ − T T s + 1 + 1 s ] = L − 1 [ − T T s + 1 ] + L − 1 [ 1 s ] = L − 1 [ − 1 s + 1 T ] + L − 1 [ 1 s ] = − e − t T + 1 \begin{align*} x_{o}(t)&=\mathcal{L}^{-1}\left[\frac{1}{Ts+1}\frac{1}{s}\right]\\&=\mathcal{L}^{-1}\left[-\frac{T}{Ts+1}+\frac{1}{s}\right]\\&=\mathcal{L}^{-1}\left[-\frac{T}{Ts+1}\right]+\mathcal{L}^{-1}\left[\frac{1}{s}\right]\\&=\mathcal{L}^{-1}\left[-\frac{1}{s+\frac{1}{T}}\right]+\mathcal{L}^{-1}\left[\frac{1}{s}\right]\\&=-e^{-\frac{t}{T}}+1 \end{align*} xo(t)=L−1[Ts+11s1]=L−1[−Ts+1T+s1]=L−1[−Ts+1T]+L−1[s1]=L−1[−s+T11]+L−1[s1]=−e−Tt+1
对于一阶惯性系统,其时间常数为:
T T T
时间常数反映的是系统的固有特性,系统的时间常数越大,惯性越小,响应的快速性越高。
计算:
X i ( s ) = sin ω t X_i(s)=\sin \omega t Xi(s)=sinωt
那么,我们就有:
x o ( t ) = L − 1 [ 1 T s + 1 ⋅ ω s 2 + ω 2 ] = L − 1 [ − T 1 + ( T ω ) 2 s s 2 + ω 2 + − 1 1 + ( T ω ) 2 ω s 2 + ω 2 + ω T 2 1 + ( T ω ) 2 T s + 1 ] = − T 1 + ( T ω ) 2 L − 1 [ s s 2 + ω 2 ] − 1 1 + ( T ω ) 2 L − 1 [ ω s 2 + ω 2 ] + ω T 2 1 + ( T ω ) 2 L − 1 [ 1 T s + 1 ] = − T 1 + ( T ω ) 2 cos ( ω t ) − 1 1 + ( T ω ) 2 sin ( ω t ) + ω T 1 + ( T ω ) 2 e − t T \begin{align*} x_{o}(t)&=\mathcal{L}^{-1}\left[\frac{1}{Ts+1}\cdot\frac{\omega }{s^2+\omega^2}\right]\\ &=\mathcal{L}^{-1}\left[\frac{-\frac{T}{1+(T\omega)^2}s}{s^2+\omega^2} + \frac{-\frac{1}{1+(T\omega)^2}\omega}{s^2+\omega^2} + \frac{\frac{\omega T^2}{1+(T\omega)^2}}{Ts+1}\right]\\ &= -\frac{T}{1+(T\omega)^2}\mathcal{L}^{-1}\left[\frac{s}{s^2+\omega^2}\right] - \frac{1}{1+(T\omega)^2}\mathcal{L}^{-1}\left[\frac{\omega}{s^2+\omega^2}\right] + \frac{\omega T^2}{1+(T\omega)^2}\mathcal{L}^{-1}\left[\frac{1}{Ts+1}\right]\\ &= -\frac{T}{1+(T\omega)^2}\cos(\omega t) - \frac{1}{1+(T\omega)^2}\sin(\omega t) + \frac{\omega T}{1+(T\omega)^2}e^{-\frac{t}{T}} \end{align*} xo(t)=L−1[Ts+11⋅s2+ω2ω]=L−1 s2+ω2−1+(Tω)2Ts+s2+ω2−1+(Tω)21ω+Ts+11+(Tω)2ωT2 =−1+(Tω)2TL−1[s2+ω2s]−1+(Tω)21L−1[s2+ω2ω]+1+(Tω)2ωT2L−1[Ts+11]=−1+(Tω)2Tcos(ωt)−1+(Tω)21sin(ωt)+1+(Tω)2ωTe−Tt
二阶系统的时域分析
类似地,我们这里着重强调二阶系统的性能指标:
t r = π − β ω d t_r=\frac{\pi -\beta}{\omega_d} tr=ωdπ−β
t p = π ω d t_p=\frac{\pi }{\omega_d} tp=ωdπ
M p = x ( t p ) − x o ( ∞ ) x o ( ∞ ) = e − π tan β M_p=\frac{x(t_p)-x_o(\infty)}{x_o(\infty )}=e^{-\frac{\pi}{\tan \beta}} Mp=xo(∞)x(tp)−xo(∞)=e−tanβπ
衰减时间
σ = 1 ζ ω n \sigma=\frac{1}{\zeta \omega_n} σ=ζωn1
调整时间
t s = 4 σ , Δ = 2 % t_s=4\sigma,\Delta =2\% ts=4σ,Δ=2%
t s = 3 σ , Δ = 5 % t_s=3\sigma,\Delta =5\% ts=3σ,Δ=5%
高阶系统的时域分析
找主导极点,将其视为二阶系统一对共轭复数极点进行进行近似处理:距虚轴最近、实部的绝对值为其它极
点实部绝对值的1/5或更小,且其附近没有零点的闭环极点。
偏差与误差
偏差定义为:
ε ( t ) = x i ( t ) − b ( t ) \varepsilon(t)=x_{i}(t)-b(t) ε(t)=xi(t)−b(t)
误差定义为:
e ( t ) = x o r ( t ) − x o ( t ) e(t)=x_{or}(t)-x_{o}(t) e(t)=xor(t)−xo(t)
推导误差与偏差的关系
E ( s ) = X i ( s ) − H ( s ) X o ( s ) E(s) =X_i(s)-H(s)X_o(s) E(s)=Xi(s)−H(s)Xo(s)
当无偏差时,系统为期望输出:
X o r ( s ) = X o ( s ) , E ( s ) = 0 X_{or}(s)=X_{o}(s),E(s)=0 Xor(s)=Xo(s),E(s)=0
所以:
H ( s ) X o r ( s ) = X i ( s ) H(s)X_{or}(s)=X_i(s) H(s)Xor(s)=Xi(s)
则有:
E 1 ( s ) = H ( s ) E ( s ) E_1(s)=H(s)E(s) E1(s)=H(s)E(s)
推导有干扰情况下的误差和偏差
E 1 ( s ) = X o r ( s ) − X o ( s ) = X i ( s ) H ( s ) − ( X o X i ( s ) + X o N ( s ) ) E_1(s)=X_{or}(s)-X_o(s)=\frac{X_i(s)}{H(s)}-\left(X_{oX_i}(s)+X_{oN}(s)\right) E1(s)=Xor(s)−Xo(s)=H(s)Xi(s)−(XoXi(s)+XoN(s))
稳态偏差与偏差系数
首先,偏差与输入之间的放大函数为:
1 1 + G ( s ) H ( s ) \frac{1}{1+G(s)H(s)} 1+G(s)H(s)1
考虑最小相位系统:
G K ( s ) = G ( s ) H ( s ) = K ∏ ( 1 + τ s ) s ν ∏ ( 1 + T s ) G_{K}(s)=G(s)H(s)=\frac{K\prod (1+\tau s)}{s^{\nu}\prod (1+Ts)} GK(s)=G(s)H(s)=sν∏(1+Ts)K∏(1+τs)
ε s s = lim s → 0 s ν + 1 s ν + K X i ( s ) \varepsilon_{ss}=\lim_{s\to 0}\frac{s^{\nu+1}}{s^{\nu}+K}X_{i}(s) εss=s→0limsν+Ksν+1Xi(s)
无偏系数记为
K ν = lim s → 0 s ν G ( s ) H ( s ) K_{\nu}=\lim_{s\to 0}s^{\nu}G(s)H(s) Kν=s→0limsνG(s)H(s)
例题
例1 已知某一阶系统的单位阶跃响应曲线如下,求该系统的传递函数 G ( s ) G(s) G(s)。
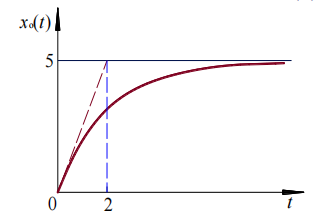
解
注意它只说是一阶系统,所用用一阶微分方程描述的系统都叫一阶系统,而非只有惯性环节
x o ( t ) = K ( 1 − e t T ) x_o(t)=K(1-e^{\frac{t}{T}}) xo(t)=K(1−eTt)
或者:
x o ′ ( 0 ) = lim s → ∞ K s T s + 1 x^{\prime}_o(0)=\lim_{s\to \infty} \frac{Ks}{Ts+1} xo′(0)=s→∞limTs+1Ks
x o ( ∞ ) = 5 = lim s → 0 K T s + 1 x_{o}(\infty)=5=\lim_{s\to 0}\frac{K}{Ts+1} xo(∞)=5=s→0limTs+1K
例2
如图(a)所示的机械系统,在质块$m 上施加, 上施加, 上施加,x_i(t)=8.9\text{N} 阶跃力后, 阶跃力后, 阶跃力后,m 的时间响应 的时间响应 的时间响应x_o(t) 如图 ( b ) 所示,试求系统的 如图(b)所示,试求系统的 如图(b)所示,试求系统的m 、 、 、k 和 和 和c $值。
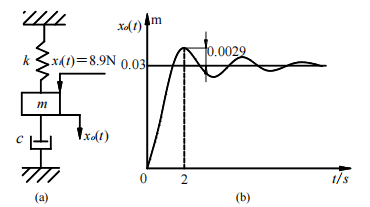
解
由于比例环节只对输出的稳态值有影响,由此:
M p = e − π tan β = 0.0029 0.03 ⇒ ζ M_p=e^{-\frac{\pi}{\tan \beta}}=\frac{0.0029}{0.03} \Rightarrow \zeta Mp=e−tanβπ=0.030.0029⇒ζ
t r = π ω d → ω n t_r=\frac{\pi }{\omega_d}\rightarrow \omega_n tr=ωdπ→ωn
lim s → 0 s m s 2 + c s + k 8.9 s = 0.03 \lim_{s\to 0}\frac{s}{ms^2+cs+k}\frac{8.9}{s}=0.03 s→0limms2+cs+kss8.9=0.03
例3
有一位置随动系统,其方框图如下图(a)所示。当系统输入单位阶跃函数时, M p ≤ 5 % M_p \leq 5\% Mp≤5%,试
(1)校核该系统的各参数是否满足要求;
(2)在(a)系统中增加一微分负反馈,如图(b)示,求其时间常数 τ \tau τ。
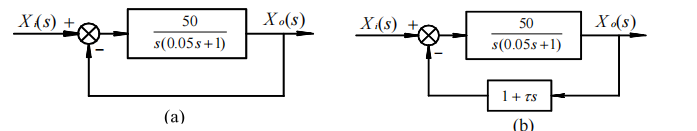
解
设前向通道的传递函数为:
G ( s ) G(s) G(s)
反馈增益为:
H ( s ) H(s) H(s)
闭环传递函数为:
G B ( s ) = G ( s ) 1 − H ( s ) G_B(s)=\frac{G(s)}{1-H(s)} GB(s)=1−H(s)G(s)
再有:
M p = e − π tan β ≤ 5 % M_p=e^{-\frac{\pi}{\tan \beta}}\leq 5\% Mp=e−tanβπ≤5%
例4 已知某单位反馈系统 G K ( s ) = 12 ( s + 1 ) s 2 ( s + 4 ) G_K(s) = \frac{12(s+1)}{s^2(s+4)} GK(s)=s2(s+4)12(s+1),试求在参考输入 x i ( t ) = 4 + 6 t + 3 t 2 x_i(t) = 4 + 6t + 3t^2 xi(t)=4+6t+3t2 作用下系统的稳态误差。
解
lim s → 0 G K ( s ) = ∞ \lim_{s\to 0}G_K(s)=\infty s→0limGK(s)=∞
lim s → 0 s G K ( s ) = ∞ \lim_{s\to 0}sG_K(s)=\infty s→0limsGK(s)=∞
lim s → 0 s 2 G K ( s ) = 3 \lim_{s\to 0}s^2G_K(s)=3 s→0lims2GK(s)=3
e s s = ε s s = a 0 1 + ∞ + a 1 ∞ + a 2 3 = 2 e_{ss}=\varepsilon_{ss}=\frac{a_0}{1+\infty}+\frac{a_1}{\infty}+\frac{a_2}{3}=2 ess=εss=1+∞a0+∞a1+3a2=2
另外的解法
K = lim s → 0 G k ( s ) K=\lim_{s\to 0}G_k(s) K=s→0limGk(s)
ν = 开环传递函数的积分环节 \nu=开环传递函数的积分环节 ν=开环传递函数的积分环节
例5
系统方框图如下图,求当 x i ( t ) = n ( t ) = 1 ( t ) x_i(t)=n(t)=1(t) xi(t)=n(t)=1(t)时,系统的 e ss e_{\text{ss}} ess。
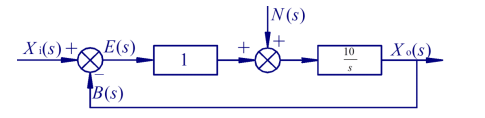
解
E ( s ) E(s) E(s)与 X i ( s ) X_i(s) Xi(s)之间的放大函数:
E ( s ) = X i ( s ) − B ( s ) = X i ( s ) − 10 s + 10 X i ( s ) − 10 s 1 + 10 s N ( s ) E(s)=X_i(s)-B(s)=X_i(s)-\frac{10}{s+10}X_i(s)-\frac{\frac{10}{s}}{1+\frac{10}{s}}N(s) E(s)=Xi(s)−B(s)=Xi(s)−s+1010Xi(s)−1+s10s10N(s)
对于单位负反馈:
ε s s = lim s → 0 s ( X i ( s ) − 10 s + 10 X i ( s ) − 10 s 1 + 10 s N ( s ) ) = − 1 \varepsilon_{ss}=\lim_{s\to 0}s\left(X_i(s)-\frac{10}{s+10}X_i(s)-\frac{\frac{10}{s}}{1+\frac{10}{s}}N(s)\right)=-1 εss=s→0lims(Xi(s)−s+1010Xi(s)−1+s10s10N(s))=−1
另外的解法
叠加定理:
[
\varepsilon_{\text{ss}} = \varepsilon_{\text{ss}X} + \varepsilon{\text{ss}_N}
]
-
对于输入( x_i(t)=1(t) ),系统为Ⅰ型系统,位置误差系数( K_p = \infty ),因此:
[
\varepsilon_{\text{ss}_X} = \frac{1}{1+K_p} = \frac{1}{1+\infty} = 0
] -
计算扰动引起的稳态误差( \varepsilon_{\text{ss}N} ),由终值定理:
[
\varepsilon{\text{ss}N} = \lim{s \to 0} s \cdot \frac{-\frac{10}{s}}{1+\frac{10}{s}} \cdot \frac{1}{s} = \lim_{s \to 0} \frac{-10}{s+10} = -1
] -
因( H(s)=1 ),故系统稳态误差:
[
e_{\text{ss}} = \varepsilon_{\text{ss}} = \varepsilon_{\text{ss}X} + \varepsilon{\text{ss}_N} = -1
]
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)