贪心算法之哈夫曼编码(C语言实现)
如题问题描述:现有一个文本文件,其中包含的字符数据出现的次数各不相同,先要求对该文本中包含的字符进行编码,使文本占用的位数更小。问题分析:我们知道文件的存储都是以二进制数表示的,如:字符c可以表示为010101…之类的。因为不同的操作系统对于不同的数据类型会分配给相同的数据容器长度,如C中int型数据固定占用4个字节的存储空间。现在问题时因为各个字符出现的概率不同,那么我们就可以给出现概率高的字符
·
如题
问题描述:现有一个文本文件,其中包含的字符数据出现的次数各不相同,先要求对该文本中包含的字符进行编码,使文本占用的位数更小。
问题分析
我们知道文件的存储都是以二进制数表示的,如:字符c可以表示为010101…之类的。因
为不同的操作系统对于不同的数据类型会分配给相同的数据容器长度,如C中int型数据固定占用4个字节
的存储空间。现在问题时因为各个字符出现的概率不同,那么我们就可以给出现概率高的字符分配以”短
“的二进制表示数,给出现概率低的字符分配以”长”的二进制表示数。从而达到降低平均每字符占用的空
间数,进而实现无损的空间压缩。
OK,我们来论证哈夫曼编码问题的贪心选择性质。这里必须介绍一下的是,我们会使用二叉树这种数
据结构来解哈夫曼问题。从根节点到叶节点经过的路径就是某个叶节点对象(这里就是字符)的编码值。
那么从直觉(恩,直觉,我觉的解贪心算法的话,直觉很重要)上将讲,应该将概率低的元素放置到树的
底部,将概率高的元素放置到树的顶部。
解题步骤
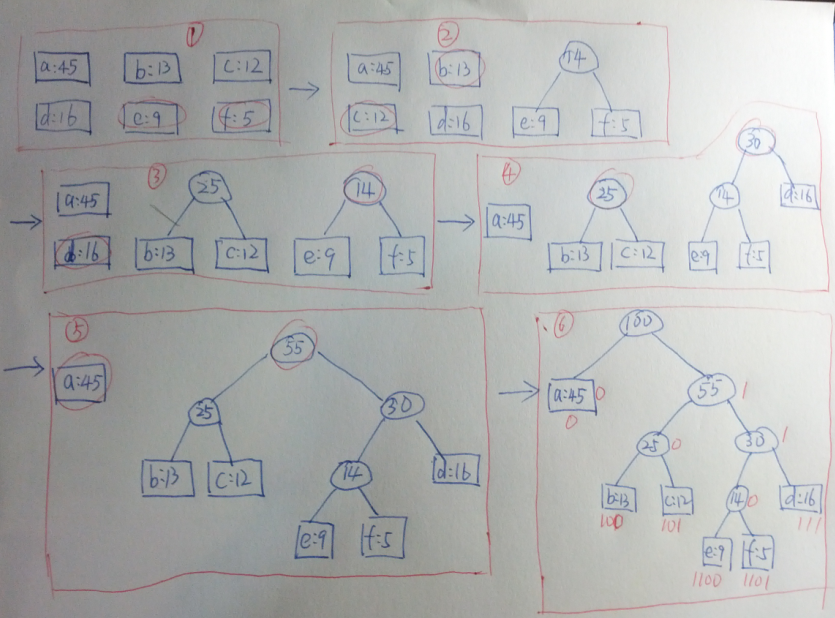
由题意可知,字符有对应的频率,这可以当做树的权重方便计算,主要思路通过每次查找最小权和次小
权构建叶子节点,俩者的和作为父节点的权值,如此循环下来构成一棵完全二叉树,对应的左子树编码
为0,右子树编码为1,通过遍历树即可得出最终的哈夫曼编码。具体代码实现如下
#define maxn 1000
struct huffnode
{
char ch; //字符
int weight; //权值
int parent; //父节点下标
int lchild;
int rchild;
}HTree[maxn*2];
char *HCode[maxn*2];
/* 创建最优二叉树 */
/* 数组c[0..n-1]和w[0..n-1]存放了n个字符及其概率,构造Huffman树HT */
void select(int n, int &r1, int &r2)
{
int minx1 = -1, ans1 = -1, ans2 = -1;
for(int i = 1; i <= n; i++)
{
if(HT[i].parent == 0)
{
if(minx1 < 0 || HTree[i].weight < minx1)
{
minx1 = HTree[i].weight;
ans1 = i;
}
}
}
minx1 = -1;
for(int i = 1; i <= n; i++)
{
if(HTree[i].parent == 0 && i != ans1)
{
if(minx1 < 0 || HTree[i].weight < minx1)
{
minx1 = HTree[i].weight;
ans2 = i;
}
}
}
r1 = ans1;
r2 = ans2;
}
void createHTree(char c[], int w[], int n )
{
int i, s1, s2;
if (n <= 1)
return;
/* 根据n个权值构造n棵只有根结点的二叉树 */
for (i=1; i<=n; i++)
{
HTree[i].ch = c[i-1];
HTree[i].weight = w[i-1];
HTree[i].parent = HTree[i].lchild = HTree[i].rchild = 0;
}
for (; i<2*n; ++i)
{
HTree[i].ch = '0';
HTree[i].parent = 0;
HTree[i].lchild = 0;
HTree[i].rchild = 0;
}
/* 构造Huffman树 */
for (i=n+1; i<2*n; i++)
{
/* 从HT[1..i-1]中选择parent为0且weight最小的两棵树,其序号为s1和s2 */
select(i-1,s1,s2);
HTree[s1].parent = i;
HTree[s2].parent = i;
HTree[i].lchild = s1;
HTree[i].rchild = s2;
HTree[i].weight = HTree[s1].weight + HTree[s2].weight;
}
}
/* n个叶子结点在Huffman树HT中的下标为1~n */
/* 第i(1<= i <= n)个叶子的编码存放HC[i]中 */
void HuffmanCoding(int n)
{
char *cd;
int i, start, c, f;
if (n<=1)
return;
/* 分配n个字节的内存,用来存放当前得到的编码 */
/* n个叶子结点最大的编码长度为n所以分配n个字节 */
cd = (char*)malloc(n);
cd[n-1] = '\0';
for (i=1; i <= n; i++)
{
start = n-1;
for (c = i,f = HTree[c].parent; f != 0; c = f, f = HTree[f].parent)
{
/**
c获取结点的下标,f获取其父母,如果其父母的左孩子下标与c相等,说明处于左子树,填0
,否则在右子树,填1,然后c跳到父母
*/
if (HT[f].lchild == c)
cd[--start] = '0';
else
cd[--start] = '1';
}
/* 从叶子结点开始查找编码
叶子结点的父结点的左子树为叶子结点,则编码为0
否则就为父结点的右子树,则编码为1 */
/* 分配内存,分配内存的字节数为当前得到的字符编码数 */
HCode[i] = (char*)malloc(n-start);
strcpy(HCode[i], &cd[start]);
}
free(cd);
}
代码中已经给出了相当多的注释,一来方便读者理解,二来是为了以后更好的复习,每日一算法,坚持便是永恒!!
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)