压缩感知——简介

压缩感知，compressed sensing又称compressed sampling，是在采样过程中完成了数据压缩的过程。
压缩感知在信号采样的过程中，用很少的采样点，实现了和全采样一样的效果。

压缩感知——信号采样

学过通信原理或信号与系统的都知道奈奎斯特采样定理，即想让采样之后的数字信号完整保留原始信号中的信息，采样频率必须大于信号中最高频率的2倍。原因是时域以τ为间隔进行采样，频域会以1/τ为周期发生周期延拓。那么如果采样频率低于两倍的信号最高频率，信号在频域频谱搬移后就会发生混叠。
2004年，Candes，陶哲轩和Donoho提出了压缩感知理论，该理论认为：如果信号是稀疏的，那么它可以由远低于采样定理要求的采样点重建恢复。
突破的关键就在于采样的方式。当我们说“采样频率”的时候，意味着做的是等间距采样，数字信号领域通常都是做等间距采样，也服从奈奎斯特采样定律。

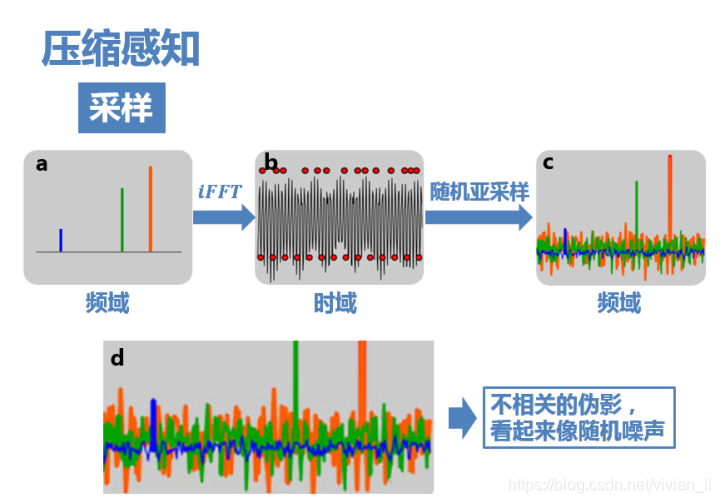
但是压缩感知采用不等间距采样，比如采用随机亚采样（图b上方的红点），那么这时候频域就不再是以固定周期进行延拓了，而是会产生大量不相关（incoherent）的干扰值。如图c，最大的几个峰值还依稀可见，只是一定程度上被干扰值覆盖。这些干扰值看上去非常像随机噪声，但实际上是由于三个原始信号的非零值发生能量泄露导致的（不同颜色的干扰值表示它们分别是由于对应颜色的原始信号的非零值泄露导致的）
之所以随机亚采样会有这样的效果，可以理解成随机采样使得频谱不再是整齐地搬移，而是一小部分一小部分胡乱地搬移，频率泄露均匀地分布在整个频域，因而泄漏值都比较小，从而有了恢复的可能。

压缩感知——信号恢复

压缩感知——两个前提条件

刚刚的例子之所以能够实现最终信号的恢复，是因为它满足了两个前提条件：

1. 这个信号在频域只有3个非零值，所以可以较轻松地恢复出它们。
2. 采用了随机亚采样机制，因而使频率泄露均匀地分布在整个频域。
   这两点对应了CS的两个前提条件——稀疏性（sparsity）、不相关性（incoherence）。
   稀疏性可以简单直观地理解为：若信号在某个域中只有少量非零值，即信号在某个域中非零点远远小于信号总点数，那么它在该域稀疏，该域也被称为信号的稀疏域。
   因此，第一个前提条件要求信号必须在某一个变换域具有稀疏性。比如例子中，信号在频域是稀疏的，因而可以通过所述的重建方法轻松地在稀疏域（频域）复原出原信号。
   然而通常信号在变换域中不会呈现完全的稀疏性。其实只要它近似满足稀疏性，即大部分值趋于零，只有少量大的非零值，就可以认为它是可压缩信号，可以对它进行CS亚采样。
   对于之前讲的例子，如果它在频域中不稀疏，我们可以做DWT、DCT等，找到它的稀疏变换。

前提条件1——稀疏性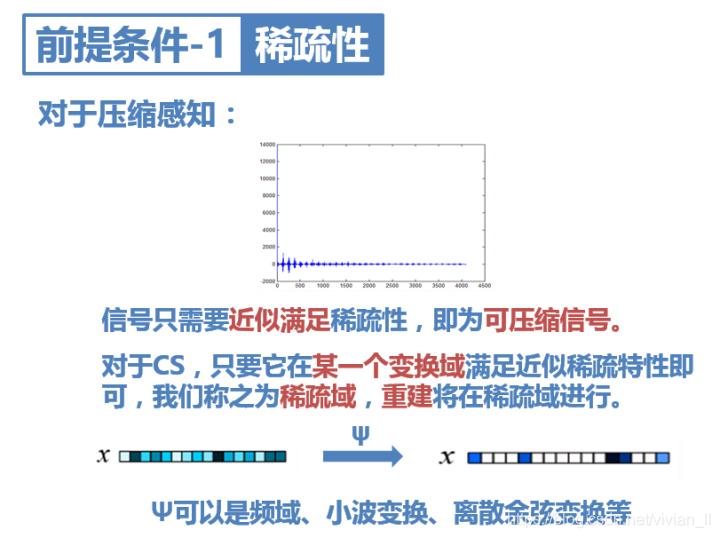

前提条件2——非相关性/等距约束性

在讲第二个前提条件之前，需要引入必要的数学表达。

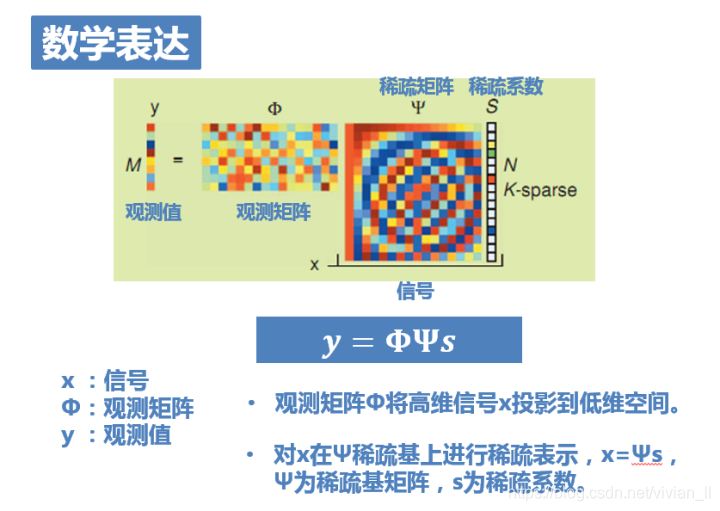
上面这张图把亚采样的过程用矩阵的方式表达出来：
如图，x是为长度N的一维信号，也就是原信号，稀疏度为k。此刻它是未知的。
Φ为观测矩阵，对应着亚采样这一过程。它将高维信号x投影到低维空间，是已知的。
y=Φx为长度M的一维测量值，也就是亚采样后的结果。显然它也是已知的。
因此，压缩感知问题就是在已知测量值y和测量矩阵Φ的基础上，求解欠定方程组y=Φx得到原信号x。
然而，一般的自然信号x本身并不是稀疏的，需要在某种稀疏基上进行稀疏表示。令x=Ψs，Ψ为稀疏基矩阵，s为稀疏系数。
于是最终方程就变成了：y=ΦΨs。已知y、Φ、Ψ，求解s。
y=ΦΨs有点长，我们把ΦΨ合并成一个矩阵，称之为传感矩阵。即令Θ=ΦΨ ，则y=ΘS。问题即为，已知y和Θ，求解S。
对应到一开始的例子中：
x就是三个正弦信号叠加在一起的原信号a；
稀疏矩阵Ψ就是傅里叶变换，将信号变换到频域S；
观测矩阵Φ就是我们采用的随机亚采样方式；
y就是最终的随机亚采样的结果c。

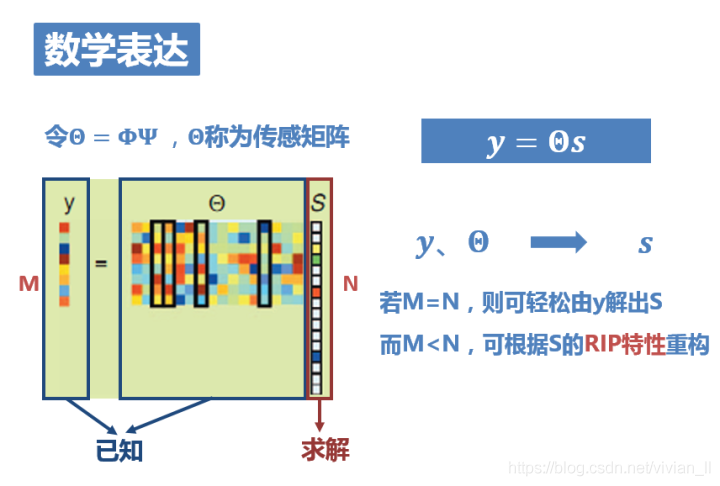
求解出S后，由x=Ψs即可得到恢复出的原信号x。
然而在正常情况下，方程的个数远小于未知数的个数，方程是没有确定解的，无法重构信号。但是，由于信号是K稀疏，如果上式中的Φ满足有限等距性质(RIP)，则K个系数就能够从M个测量值准确重构（得到一个最优解）。
陶哲轩和Candès证明了RIP是观测矩阵要满足的准确要求。但是，要确认一个矩阵是否满足RIP非常复杂。于是Baraniuk证明：RIP的等价条件是观测矩阵和稀疏表示基不相关（incoherent）。即压缩感知的第二个前提条件。


那怎样找到不相关的观测矩阵呢？陶哲轩和Candès又证明： 独立同分布的高斯随机测量矩阵可以成为普适的压缩感知测量矩阵。
于是满足高斯分布的随机测量矩阵就成了CS最常用的观测矩阵。
对于二维信号，往往就采用二维高斯随机测量采样矩阵对图像进行亚采样。
对于一维信号，采用前文提到的随机不等间距的亚采样即可。

压缩感知——重建方法

信号采样后需要将其恢复。CS的重建也就是求解欠定方程组y=ΘS的方法。这是一个零范数（l0）最小化问题，是一个NP完全问题（没有快速解法的问题），因此往往转换成一范数（l1）最小化的求解，或者用一些近似估计的算法。
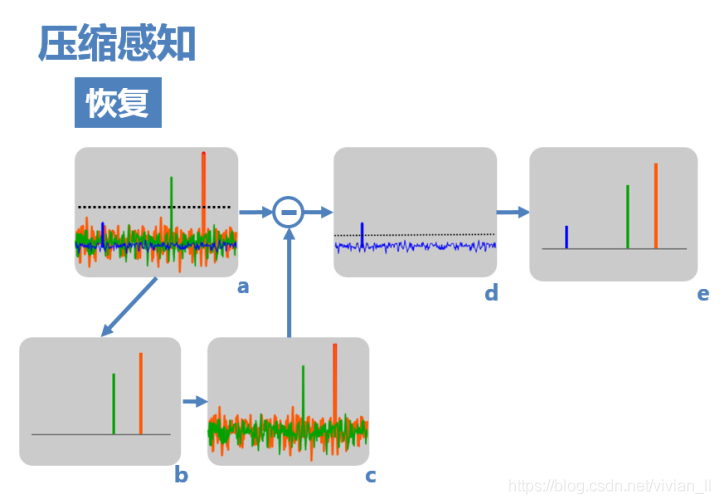
匹配追踪是一种典型的算法。以上文中的例子为例：
(1) 由于原信号的频率非零值在亚采样后的频域中依然保留较大的值，其中较大的两个可以通过设置阈值，检测出来（图a）。
(2) 然后，假设信号只存在这两个非零值（图b），则可以计算出由这两个非零值引起的干扰（图c）。
(3) 用a减去c，即可得到仅由蓝色非零值和由它导致的干扰值(图d），再设置阈值即可检测出它，得到最终复原频域（图e）
(4) 如果原信号频域中有更多的非零值，则可通过迭代将其一一解出。

扩展：图像压缩与压缩感知

信号的稀疏性已经在图像压缩领域有了很广泛的应用。利用信号的稀疏性，可以对信号进行压缩。如图像压缩领域的JPEG格式，就是将图像变换到离散余弦域，得到近似稀疏矩阵，只保留较大的值，从而实现压缩。
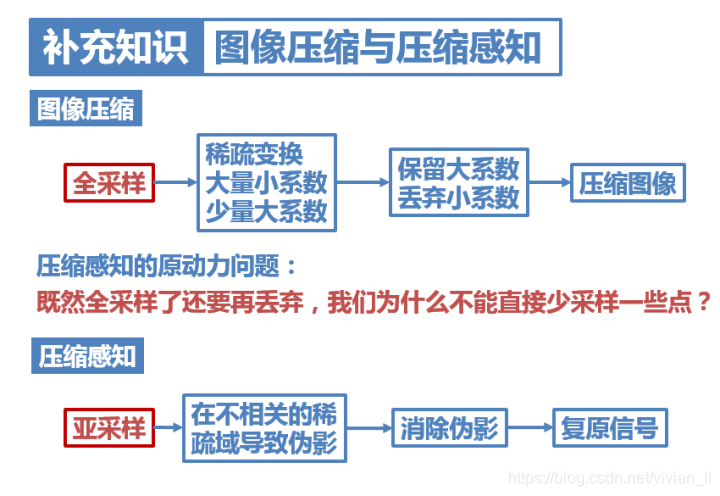
图像压缩和压缩感知这两个概念有着本质上的区别。
图像压缩是先进行了全采样，然后再变换域丢弃小系数，完成压缩；
而压缩感知不同，它的思想其实从图像压缩中借鉴了很多：既然全采样了还要再丢弃，我们为什么不能直接少采样一些点？因此，压缩感知直接进行了亚采样，然后再用算法消除亚采样导致的伪影。可以说，压缩感知直接在采样时就完成了压缩。

这种直接减少采样点，采集完后重建的方式，相比于图像压缩的全采用之后再压缩的方式，对于很多情形，比如照相机拍摄照片，并没有优势。因为所有像素的采集在一瞬间就都完成了。但是对于一些采集比较慢的情形，比如核磁共振成像，CS就可以发挥巨大优势。原本一副MRI图像常常需要几十秒，速度慢也是MRI的一大缺陷。而应用CS技术后，只需要采集全采样几分之一的数据，就可以重建出原图。这样就可以把成像速度提高好几倍，同时对图像质量影响不大。

总结

什么是压缩感知：
如果一个信号在某个变换域是稀疏的，那么就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上，然后通过求解一个优化问题就可以从这些少量的投影中以高概率重构出原信号。
压缩感知理论主要包括三部分：
（1）信号的稀疏表示；
（2）设计测量矩阵，要在降低维数的同时保证原始信号x的信息损失最小；
（3）设计信号恢复算法，利用M个观测值无失真地恢复出长度为N的原始信号。

从06年提出至今，已经发展出了很多算法，原来的基于l1 minimization的BP算法很慢，现在都是快速算法，而且求解算法也从纯优化方面扩展到了estimation方面，有很多基于贝叶斯估计的方法了，目前最火的也是Donoho他们组搞得AMP算法，是用Graph model里面的message passing算法通过近似求解MMSE（MAP）解。在测量矩阵方面，也已经设计出了各种矩阵，除了i.i.d. Gaussian的矩阵还有很多正交的矩阵，比如partial random DFT/DCT 矩阵。对信号的要求也从稀疏变成了存在某种结构，比如low rank，group sparse等等。（2017年进展）

压缩感知和矩阵填充

矩阵填充的要领是通过低秩矩阵中的已知要素还原出该矩阵的其他未知要素的进程。这几年，关于矩阵填充方法的理论研究成为压缩感知技术的一个研究热点。在实际的应用领域中涉及对高维数据的分析与处理，可以运用矩阵填充的方法来解决。其过程主要是：通过观测到的局部数据来准确填充缺失数据,从而获得完整数据矩阵的过程。
压缩感知和矩阵填充都是稀疏约束下的反问题，压缩感知利用信号本身或在变换域中的稀疏约束性求解欠定方程，矩阵填充利用矩阵的低秩约束性求解欠定方程。
压缩感知理论的核心问题是信号的稀疏表示、观测矩阵的设计和重构算法，信号本身或在变换域中的系数越稀疏，观测矩阵和稀疏基构成的压缩感知矩阵的受限等距常数越小，则压缩感知的性能越好。
矩阵填充理论的核心问题是矩阵的低秩特性、非相干特性和重构算法，寻找性能良好的重构算法一直是矩阵填充理论中的一个研究重点。此外，压缩感知的应用领域已经拓展得较为广泛，但矩阵填充的应用尚处于起步阶段，挖掘矩阵填充的应用，进而将矩阵填充和压缩感知结合起来进行应用方面的探索，是非常重要和有意义的课题。
压缩感知的性能取决于3个要素：信号的稀疏性、压缩感知矩阵的非相干性和重构算法的快速有效性。
矩阵填充性能也取决于3个要素：矩阵的低秩性、矩阵的不相关性和重构算法的快速有效性。

低秩矩阵

还记得我们怎么手工求矩阵的秩吗？为了求矩阵A的秩，我们是通过矩阵初等变换把A化为阶梯型矩阵，若该阶梯型矩阵有r个非零行，那A的秩rank(A)就等于r。从物理意义上讲，矩阵的秩度量的就是矩阵的行列之间的相关性。如果矩阵的各行或列是线性无关的，矩阵就是满秩的，也就是秩等于行数。回到上面线性方程组来说吧，因为线性方程组可以用矩阵描述嘛。秩就表示了有多少个有用的方程了。上面的方程组有3个方程，实际上只有2个是有用的，一个是多余的，所以对应的矩阵的秩就是2了。
OK。既然秩可以度量相关性，而矩阵的相关性实际上就表示了矩阵的结构信息。如果矩阵之间各行的相关性很强，那么就表示这个矩阵实际可以投影到更低维的线性子空间，也就是用几个向量就可以完全表达了，它就是低秩的。所以我们总结的一点就是：如果矩阵表达的是结构性信息，例如图像、用户-商品推荐表等等，那么这个矩阵各行之间存在这一定的相关性，那这个矩阵一般就是低秩的。
如果X是一个m行n列的数值矩阵，rank(X)是X的秩，假如rank (X)远小于m和n，则我们称X是低秩矩阵。低秩矩阵每行或每列都可以用其他的行或列线性表出，可见它包含大量的冗余信息。利用这种冗余信息，可以对缺失数据进行恢复，也可以对数据进行特征提取。

应用

矩阵填充越来越多的应用在协同滤波、系统识别、无线传感网络、视频去噪、人脸识别、医学成像等领域，正在发挥着巨大的作用。特别是在室内定位中的 应用越来越多，是当下的研究热点之一。

参考网址：
形象易懂讲解算法II——压缩感知（非常好）
AndyJee：浅谈压缩感知系列——博客园（非常丰富）
压缩感知理论
机器学习——低秩矩阵分解中低秩的意义、矩阵填补、交叉验证