L2/L1正则化方法，就是最常用的正则化方法，它直接来自于传统的机器学习。

L2正则化方法如下：

L1正则化方法如下：

那它们俩有什么区别呢？最流行的一种解释方法来自于模式识别和机器学习经典书籍，下面就是书中的图。

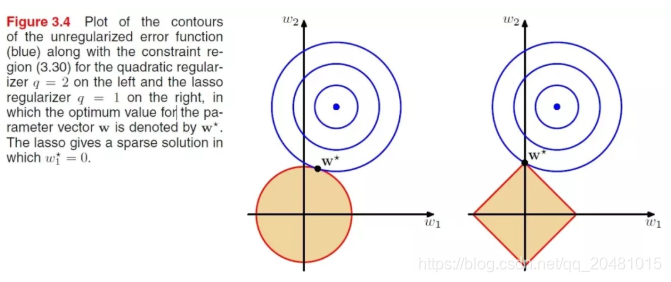
这么来看上面的那张图，参数空间(w1,w2)是一个二维平面，蓝色部分是一个平方损失函数，黄色部分是正则项。

蓝色的那个圈，中心的点其实代表的就是损失函数最优的点，而同心圆则代表不同的参数相同的损失，可见随着圆的扩大，损失增大。黄色的区域也类似，周边的红色线表示的是损失相同点的轮廓。

正则项的红色轮廓线示平方损失的蓝色轮廓线总要相交，才能使得两者加起来的损失最小，两者的所占区域的相对大小，是由权重因子决定的。不管怎么说，它们总有一个交叉点。

对于L2正则化，它的交点会使得w1或者w2的某一个维度特别小，而L1正则化则会使得w1或者w2的某一个维度等于0，因此获得所谓的稀疏化。

在深度学习框架中，大家比起L1范数，更钟爱L2范数，因为它更加平滑和稳定。