1.算法介绍

最小割算法（Minimum Cut）是图像分割的经典算法之一，同时也在"Graph Cut"、"Grab Cut"等算法中都有被使用过。最小割最大流算法是指在一个有向的图中，能够从源点（source）到达汇点（terminal）的最大流量等于如果从图中剪除就能够导致网络流中断的边的集合的最小容量和。即在任何网络中，最大流的值等于最小割的容量。
提出该分割算法的论文：
Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images

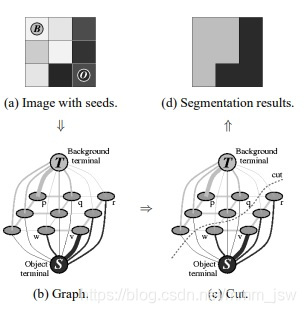
2.最小割

图论中的最小割
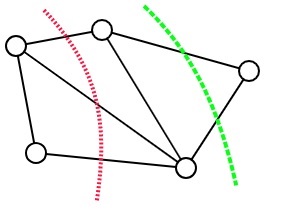
在图论中，图的最小切割是其在某种意义上是最小的切割（图形的顶点划分为由至少一个边连接的两个不相交的子集）。图的最小割可以分很多情况进行讨论，例如有向图、无向图，边的权重等。下图是一张无向无权重图和它的两个割，红色的线格割掉了三条边，而绿色的线割掉了两条边，很明显绿色的线为该图的最小割。

关于最小割
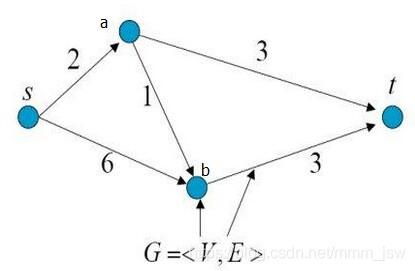
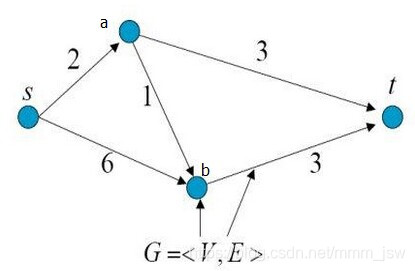
如下图1所示，是一个有向带权图，共有4个顶点和5条边。每条边上的箭头代表了边的方向，每条边上的数字代表了边的权重。

公式：$$G=<V,E>$$是图论中对图的表示方式，其中V表示顶点(vertex)所构成的集合，E表示边(edge)所构成的集合。顶点V的集合和边的集合E构成了图G(graph)。
以图1为例，图1中顶点s表示源点(source)，顶点t表示终点(terminal)，从源点s到终点t共有3条路径：

s -> a -> t
s -> b -> t
s -> a -> b-> t
现在要求剪短图中的某几条边，使得不存在从s到t的路径，并且保证所减的边的权重和最小。相信大家能很快想到解答：剪掉边”s -> a”和边”b -> t”。

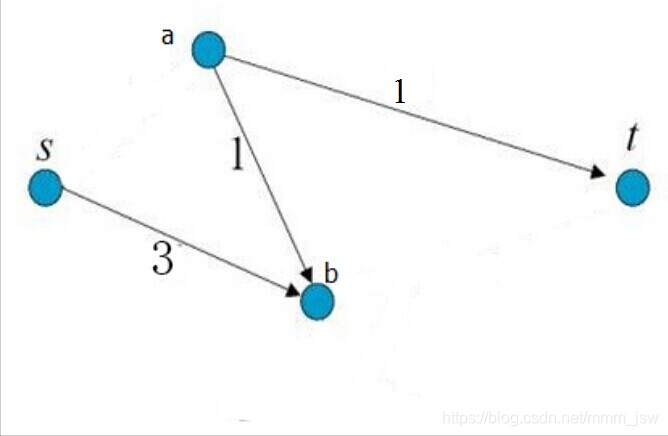
如上图2所示，图中已经不存在从源点到终点的路径，所割掉的边的权重值之和为5，是所有的切割方式中权重值最小的，像这样的切割方法我们将其称之为最小割。

3.最大流

如图所示，假如顶点s源源不断有水流出，边的权重代表该边允许通过的最大水流量，顶点t流入的水流量最大是多少？

我们可以从顶点s到顶点t的3条路径着手分析，从源点s到终点t共有3条路径：
s -> a -> t：流量被边”s -> a”限制，最大流量为2
s -> b -> t：流量被边”b -> t”限制，最大流量为3
s -> a -> b-> t：边”s -> a”的流量已经被其他路径占满，没有流量
所以，顶点t能够流入的最大水流量为：2 + 3 = 5。
这就是最大流问题。所以，图1的最大流为：2 + 3 = 5。
可以发现图1的最小割和最大流都为5，经过数学证明可以知道，图的最小割问题可以转换为最大流问题。所以，算法上在处理最小割问题时，往往先转换为最大流问题。

最大流和最小割的关系是什么？
1.最大流不可能大于最小割，因为最大流所有的水流都一定经过最小割那些割边，流过的水流怎么可能比水管容量还大呢？
2.最大流不可能小于最小割，如果小，那么说明水管容量没有物尽其用，可以继续加大水流。
由此可见，最大流和最小割的其实都是在求解同一个问题。

最大流的求解方式
最小割最大流的一种详细的解释
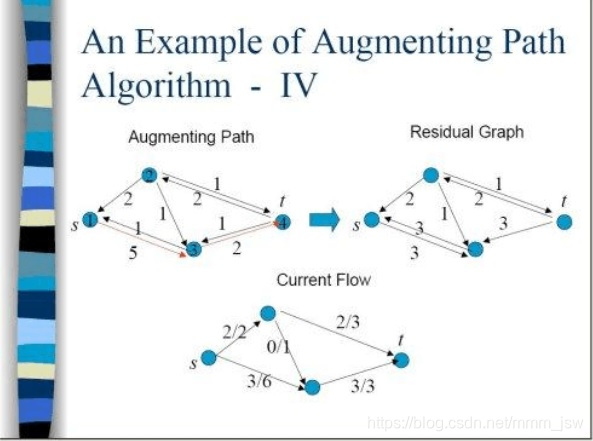
下面介绍最大流的求解过程：
Step 1：1->2->3->4（s->t的路径）

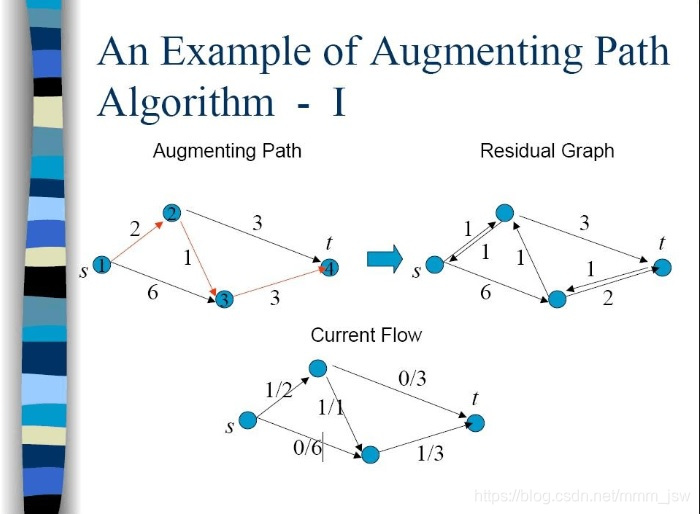
Step 2：1->2->3（s->t的路径）

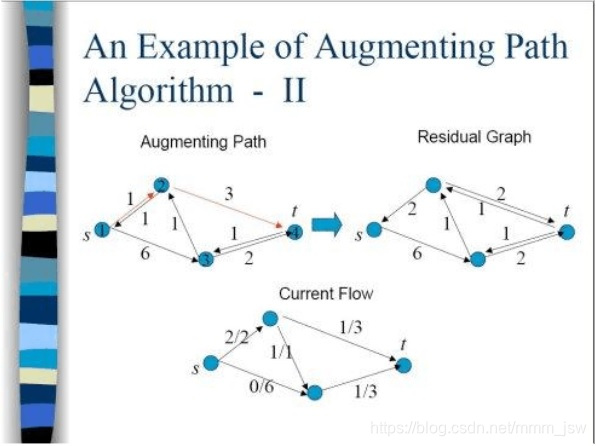
Step 3： 1->3->2->4（s->t的路径，其中2-3的方向在之前已经反向）

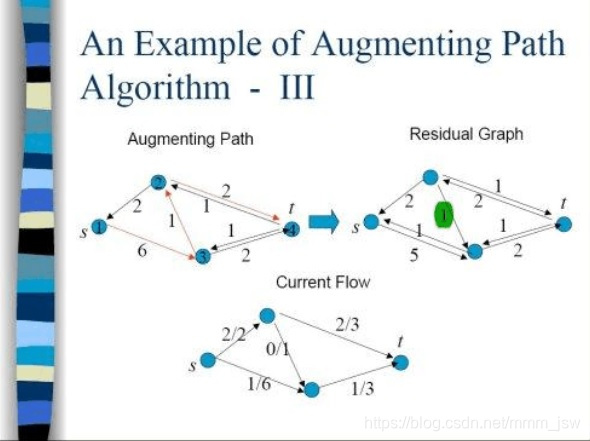
Step 4： 1->3->4（s->t的路径）

4.参考内容

1.图像分割之最小割与最大流算法：
https://imlogm.github.io/%E5%9B%BE%E5%83%8F%E5%A4%84%E7%90%86/mincut-maxflow/
2.最大流-最小割问题：
https://wenku.baidu.com/view/54323c030722192e4536f64f.html?re=view