ECC椭圆曲线加解密原理详解(配图)

本文主要参照：ECC加密算法入门介绍及 ECC椭圆曲线详解(有具体实例)

前言： 椭圆曲线(ECC)加密原理跟RSA加解密原理比起来，可真是晦涩难懂。拜读了Kalafinaian的文章“ECC椭圆曲线详解(有具体实例)”，终于看到了参透的曙光。 由于原文中有微小的瑕疵，也为了便于阅读起来更加流畅，我重新整理了一下这篇文章。

为什么使用椭圆曲线加密算法？

RSA的解决分解整数问题需要亚指数时间复杂度的算法，而目前已知计算椭圆曲线离散对数问题(ECDLP)的最好方法都需要全指数时间复杂度。这意味着在椭圆曲线系统中我们只需要使用相对于RSA 短得多的密钥就可以达到与其相同的安全强度。例如，一般认为160比特的椭圆曲线密钥提供的安全强度与1024比特RSA密钥相当。使用短的密钥的好处在于加解密速度快、节省能源、节省带宽、存储空间。
比特币以及中国的二代身份证都使用了256 比特的椭圆曲线密码算法。

实数椭圆曲线

什么是椭圆曲线，想必大家都会首先想到的是高中时学到的标准椭圆曲线方程。
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b，焦点在x轴，a<b，焦点在y轴)$$

其实本文提到的椭圆曲线，跟这个高中时代的椭圆曲线方程基本无关。椭圆曲线的椭圆一词来源于椭圆周长积分公式。(这个命名深究起来比较复杂，了解一下就可以了¹)

一条椭圆曲线是在射影平面上满足威尔斯特拉斯方程（Weierstrass）所有点的集合，
$$Y^{2}Z+a_{1}XYZ+a_{3}Y{Z}^2=X^3+a_2{X}^{2}Z+a_{4}X{Z}^2+a_6{Z}^3$$
对普通平面上点(x,y)，令x=X/Z，y=Y/Z，Z≠0，得到如下方程
$$y^2{Z}^3+a_{1}xy{Z}^3+a_{3}y{Z}^3=x^3{Z}^3+a_2{x}^2{Z}^3+a_{4}x{Z}^3+a_6{Z}^3$$
约掉$Z^3$可以得到：$$y^2+a_{1}xy+a_{3}y=x^3+a_2{x}^2+a_{4}x+a_6$$

简化版的Weierstrass方程：
$$E:y^2=x^3+ax+b$$
其中，
(1) $\Delta =-16(4a^3+27b)\ne 0$ ,用来保证曲线是光滑的，即曲线的所有点都没有两个或者两个以上的不同的切线。
(2) $a,b\in K,K为E的基础域。$
(3) 点 $O_{\infty }$ 是曲线的唯一的无穷远点。

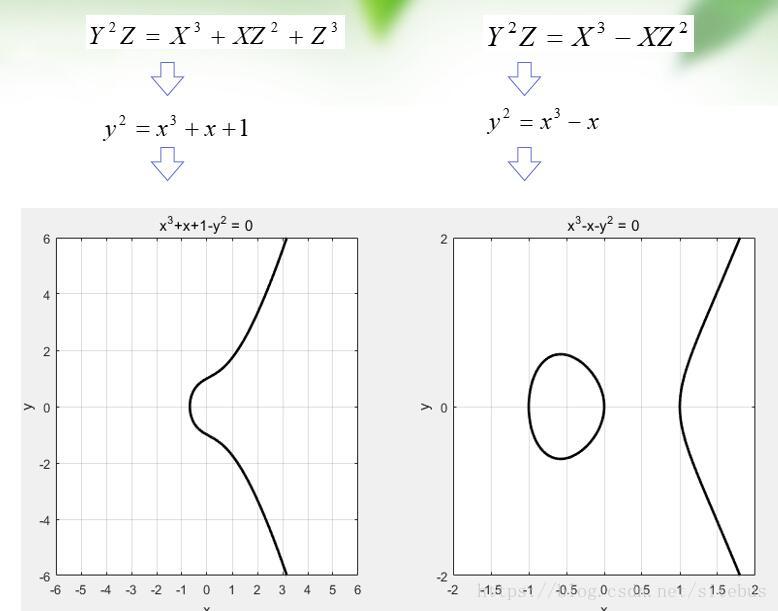
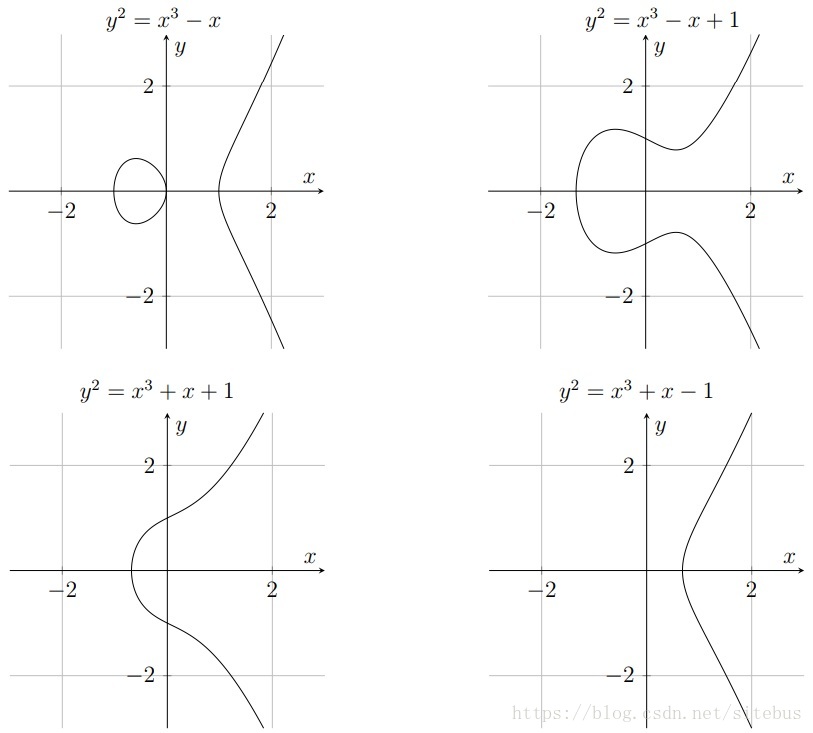
椭圆曲线示例

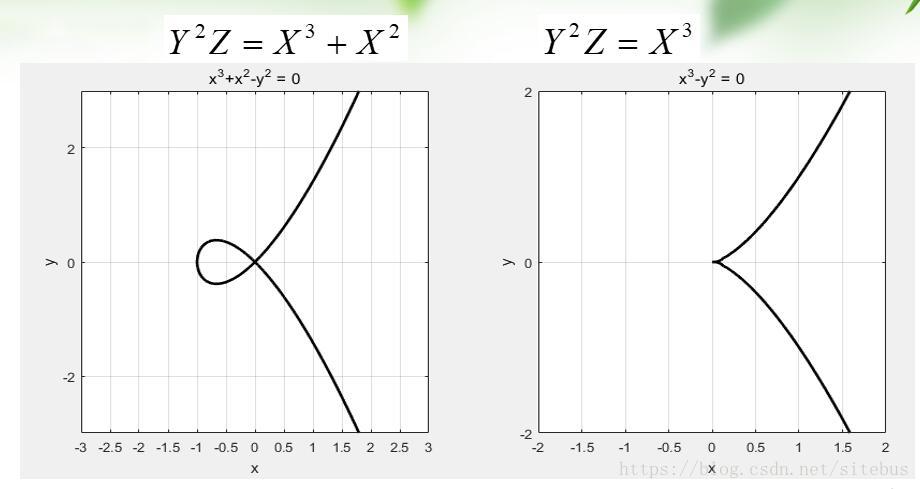
非椭圆曲线示例

这两个方程都不是椭圆曲线,因为他们在（0:0:1）点处（即原点）没有切线，不满足椭圆曲线每个点都必须是非奇异的（光滑的）

椭圆曲线阿贝尔群

我们已经看到了椭圆曲线的图象，但点与点之间好象没有什么联系。我们能不能建立一个类似于在实数轴上加法的运算法则呢？这就要定义椭圆曲线的加法群，这里需要用到近世代数中的阿贝尔群。

在数学中，群是一种代数结构，由一个集合以及一个二元运算所组成。已知集合和运算(G,*)如果是群则必须满足如下要求。

封闭性： ∀a,b∈G，ab ∈ G
结合性： ∀a,b,c∈G ，有 (ab)c = a (b*c)
单位元： ョe∈G， ∀a ∈G，有ea = ae = a
逆元： ∀a ∈G ，ョb∈G 使得 ab = ba = e
交换性: ∀a,b∈G，ab = ba

同样在椭圆曲线也可以定义阿贝尔群。
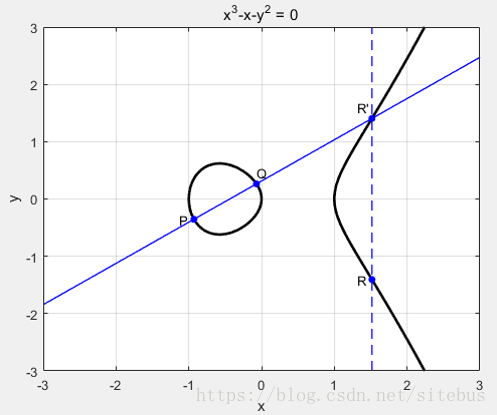
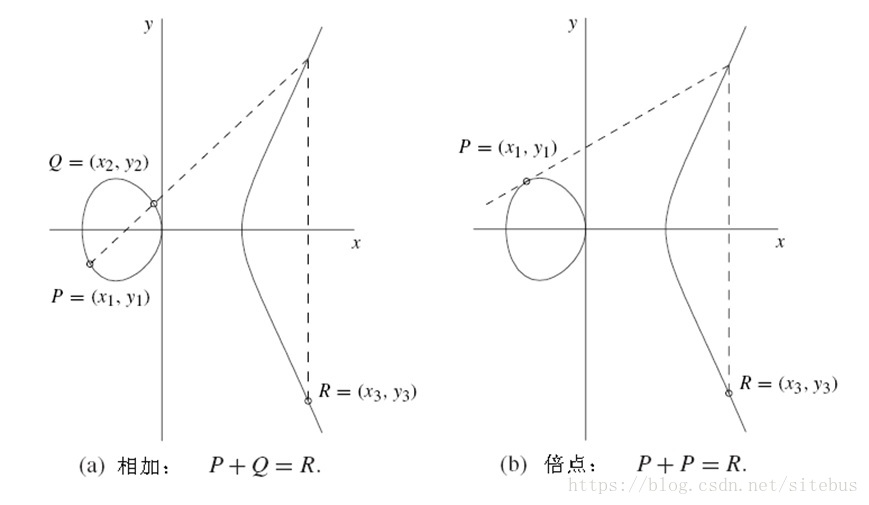
任意取椭圆曲线上两点P、Q（若P、Q两点重合，则作P点的切线），作直线交于椭圆曲线的另一点R’，过R’做y轴的平行线交于R，定义P+Q=R。这样，加法的和也在椭圆曲线上，并同样具备加法的交换律、结合律。

同点加法
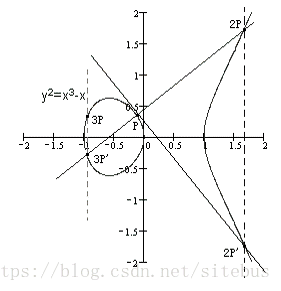
若有k个相同的点P相加，记作kP 。 P+P=2P

P+P+P=2P+P=3P

有限域椭圆曲线

椭圆曲线是连续的，并不适合用于加密；所以，我们必须把椭圆曲线变成离散的点，我们要把椭圆曲线定义在有限域上。

我们给出一个有限域Fp

• Fp中有p（p为质数）个元素0,1,2,…, p-2,p-1
• Fp的加法是$a+b\equiv c(\mathrm{m}\mathrm{o}\mathrm{d}p)$
• Fp的乘法是$a\times b\equiv c(\mathrm{m}\mathrm{o}\mathrm{d}p)$
• Fp的除法是$a÷b\equiv c(\mathrm{m}\mathrm{o}\mathrm{d}p)，即a\times b^{-1}\equiv c(\mathrm{m}\mathrm{o}\mathrm{d}p)，b^{-1}也是一个0到p-1之间的整数，但满足b\times b^{-1}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}p)$
• Fp的单位元是1，零元是 0
• Fp域内运算满足交换律、结合律、分配律
• 椭圆曲线Ep(a,b)，p为质数，x,y∈[0,p-1]

$$y^2=x^3+ax+b(\mathrm{m}\mathrm{o}\mathrm{d}p)$$

选择两个满足下列约束条件的小于p的非负整数a、b :
$$4a^3+27b^2\ne 0(\mathrm{m}\mathrm{o}\mathrm{d}p)$$

Fp上的椭圆曲线同样有加法

1.无穷远点 $O_{\infty }是零元，有O_{\infty }+O_{\infty }=O_{\infty }，O_{\infty }+P=P$
2.P(x,y)的负元是 (x,-y mod p)= (x,p-y) ，有$P+(-P)=O_{\infty }$
3.$P(x_1,y_1),Q(x_2,y_2)的和R(x_3,y_3)$ 有如下关系：
$$\begin{array}{rl}{x}_3& \equiv k^2-x_1-x_2(\mathrm{m}\mathrm{o}\mathrm{d}p)\\ y_3& \equiv k(x_1-x_3)-y_1(\mathrm{m}\mathrm{o}\mathrm{d}p)\\ & 若P=Q,则k=\frac{3x_1^2+a}{2y_1}(\mathrm{m}\mathrm{o}\mathrm{d}p)\\ & 若P\ne Q,则k=\frac{y_2-y_1}{x_2-x_1}(\mathrm{m}\mathrm{o}\mathrm{d}p)\end{array}$$

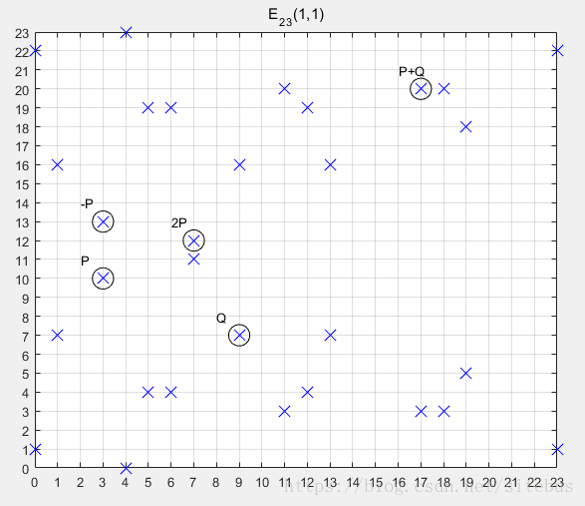
例题椭圆曲线已知E23(1,1)上两点P(3,10)，Q(9,7)，求
(1) -P
(2) P+Q
(3) 2P

(1) 计算-P
$-P=(3,-10(\mathrm{m}\mathrm{o}\mathrm{d}23))=(3,13)$
(2) 计算P+Q
$$\begin{array}{rl}k& =\frac{7-10}{9-3}=-2^{-1}(\mathrm{m}\mathrm{o}\mathrm{d}23)\\ & 2\times 2^{-1}=1(\mathrm{m}\mathrm{o}\mathrm{d}23)\\ & \Rightarrow 2^{-1}=12\\ & \Rightarrow k=-12(\mathrm{m}\mathrm{o}\mathrm{d}23)=11\\ \therefore P+Q& =(11^2-3-9(\mathrm{m}\mathrm{o}\mathrm{d}23),11\times (3-x_3)-10(\mathrm{m}\mathrm{o}\mathrm{d}23))\\ & =(17,11\times (3-17)-10(\mathrm{m}\mathrm{o}\mathrm{d}23))\\ & =(17,20)\end{array}$$
(3) 计算2P
$$\begin{array}{rl}k& =\frac{3\times 3^2+1}{2\times 10}(\mathrm{m}\mathrm{o}\mathrm{d}23)=7\times 5^{-1}(\mathrm{m}\mathrm{o}\mathrm{d}23)\\ & 5\times 5^{-1}=1(\mathrm{m}\mathrm{o}\mathrm{d}23)\\ & \Rightarrow 5^{-1}=14\\ & \Rightarrow k=7\times 14(\mathrm{m}\mathrm{o}\mathrm{d}23)=6\\ \therefore 2P& =(6^2-3-3(\mathrm{m}\mathrm{o}\mathrm{d}23),6\times (3-x_3)-10(\mathrm{m}\mathrm{o}\mathrm{d}23))\\ & =(7,6\times (3-7)-10(\mathrm{m}\mathrm{o}\mathrm{d}23))\\ & =(7,12)\end{array}$$

有限域椭圆曲线点的阶

如果椭圆曲线上一点P，存在最小的正整数n使得数乘$nP=O_{\infty }$ ,则将n称为P的阶
若n不存在，则P是无限阶的.

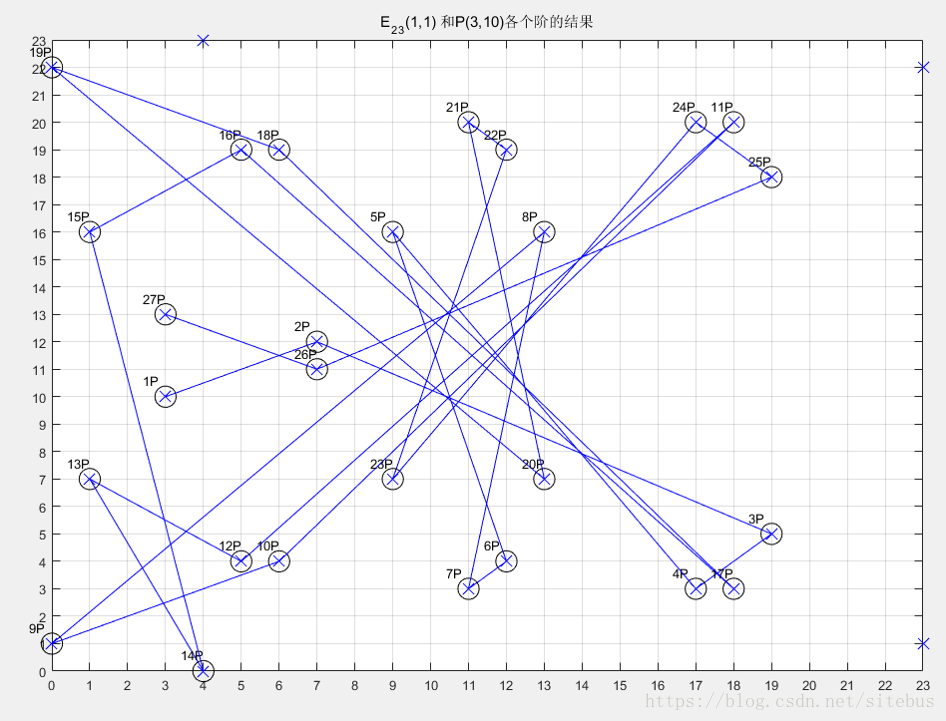
计算可得$27P=-P=(3,13)$ , 所以$28P=O_{\infty }$ P的阶为28
这些点做成了一个循环阿贝尔群，其中生成元为P，阶数为28。显然点的分布与顺序都是杂乱无章。

椭圆曲线加密

考虑$K=kG$ ，其中K、G为椭圆曲线Ep(a,b)上的点，n为G的阶（$nG=O_{\infty }$ ），k为小于n的整数。则给定k和G，根据加法法则，计算K很容易但反过来，给定K和G，求k就非常困难。因为实际使用中的ECC原则上把p取得相当大，n也相当大，要把n个解点逐一算出来列成上表是不可能的。这就是椭圆曲线加密算法的数学依据 。

• 点G称为基点（base point）
• $k(k<n)$为私有密钥（private key）
• K为公开密钥（public key)
  
  下面是利用椭圆曲线进行加密通信的过程：
  1、用户A选定一条椭圆曲线Ep(a,b)，并取椭圆曲线上一点，作为基点G。
  2、用户A选择一个私有密钥k，并生成公开密钥K=kG。
  3、用户A将Ep(a,b)和点K，G传给用户B。
  4、用户B接到信息后 ，将待传输的明文编码到Ep(a,b)上一点M（编码方法很多，这里不作讨论），并产生一个随机整数r（r<n）。
  5、用户B计算点$C_1=M+rK$和$C_2=rG$。
  6、用户B将$C_1、C_2$传给用户A。
  7、用户A接到信息后，计算$C_1-k{C}_2$，结果就是点M。再对点M进行解码就可以得到明文。
  因为$C_1-k{C}_2=M+rK-k(rG)=M+rkG-krG=M$
  

ECC保密通信算法例子

1. Alice选定一条椭圆曲线E，并取椭圆曲线上一点作为基点G 假设选定E29(4,20)，基点G(13,23) , 基点G的阶数n=37
2. Alice选择一个私有密钥k（k<n）比如25，并生成公开密钥K=kG = 25G = (14,6）
3. Alice将E和点K、G传给Bob
4. Bob收到信息后，将待传输的明文编码到E上的一点M，并产生一个随机整数r（r<n,n为G的阶数） 假设r=6 要加密的信息为3,因为M也要在E29(4,20) 上，所以M=(3,28)
5. Bob计算点$C_1$和$C_2$ $$\begin{array}{rl}{C}_1& =M+rK=M+6K=M+6G=(3,28)+6\times (14,6)=(3,28)+(27,27)=(6,12)\\ C_2& =rG=6G=(5,7)\end{array}$$
6. Bob将$C_1、C_2$传给Alice
7. Alice收到信息后，计算$C_1-k{C}_2$，结果就是 $M=C_1-k{C}_2=(6,12)-25C_2=(6,12)-25\times (5,7)=(6,12)-(27,27)=(6,12)+(27,2)=(3,28)$

ECC技术要求

通常将Fp上的一条椭圆曲线描述为T=(p,a,b,G,n,h)p、a、b确定一条椭圆曲线（p为质数，(mod p)运算）G为基点，n为点G的阶，h是椭圆曲线上所有点的个数m与n相除的商的整数部分

参量选择要求：

• p越大安全性越好，但会导致计算速度变慢
• 200bit左右可满足一般安全要求
• n应为质数 h≤4；p≠n×h ；pt≠1(mod n) (1≤t＜20)
• $4a^3+27b^2\ne 0(\mathrm{m}\mathrm{o}\mathrm{d}p)$

ECC的应用（比特币）

比特币系统选用的secp256k1中，参数为
p = 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F= $2^{256}-2^{32}-2^9-2^8-2^7-2^6-2^4-1$
a = 0， b = 7
G=(0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
n = 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
h = 01

ECC vs. RSA – ECC的优缺点

优点	缺点
安全性能更高：160位ECC与1024位RSA、DSA有相同的安全强度	设计困难，实现复杂
处理速度更快：在私钥的处理速度上，ECC远 比RSA、DSA快得多	如果序列号设计过短，那么安全性并没有想象中的完善
带宽要求更低
存储空间更小：ECC的密钥尺寸和系统参数与RSA、DSA相比要小得多

---

---

1. 椭圆曲线的名称由来：椭圆周长的计算可以转化为积分${\int }_{\alpha }^{\beta }\frac{dx}{\sqrt{x^3+ax+b}}$，分母的函数项$y=\sqrt{x^3+ax+b}$两边平方即可得到椭圆曲线方程，曲线故而得名椭圆曲线。(请参考椭圆曲线密码体制解释，这个命名深究起来很复杂，了解一下就可以了) ↩︎