交叉熵代价函数

1. 交叉熵理论

交叉熵与熵相对，如同协方差与方差。

熵考察的是单个的信息（分布）的期望：

$$H(p)=-\sum_{i=1}^n p(x_i)\log p(x_i)$$

交叉熵考察的是两个的信息（分布）的期望：

$$H(p,q)=-\sum_{i=1}^np(x_i)\log q(x_i)$$
详见 wiki Cross entropy

y = tf.placeholder(dtype=tf.float32, shape=[None, 10])

.....

scores = tf.matmul(h, w) + b
probs = tf.nn.softmax(scores) 
loss = -tf.reduce_sum(y*tf.log(probs))

2. 交叉熵代价函数

$$L_H(\mathbf x,\mathbf z)=-\sum_{k=1}^dx_k\log z_k+(1-x_k)\log(1-z_k)$$
$\mathbf x$ 表示原始信号， $\mathbf z$ 表示重构信号，以向量形式表示长度均为 $d$，又可轻易地将其改造为向量内积的形式。

3. 交叉熵与 KL 散度（也叫相对熵）

• Intuitively, why is cross entropy a measure of distance of two probability distributions?
• 熵、交叉熵、相对熵（KL 散度）意义及其关系
• 机器学习基础（五十八）—— 香农熵、相对熵（KL散度）与交叉熵

所谓相对，自然在两个随机变量之间。又称互熵，Kullback–Leibler divergence（K-L 散度）等。设 p(x) 和 q(x) 是 X 取值的两个概率分布，则 p 对 q 的相对熵为：

$$\begin{split} D_{KL}(p||q)=&\sum_{i=1}^n p(x_i)\log\frac{p(x_i)}{q(x_i)}\\ =&\sum_{i=1}^np(x_i)\log p(x_i)-\sum_{i=1}^np(x_i)\log q(x_i)\\ =&-H(p)+H(p,q) \end{split}$$

（在稀疏型自编码器损失函数的定义中，基于 KL 散度的惩罚项常常定义成如下的形式：

$$H(\rho||\hat \rho)=-\sum_{j=1}^m\left[\rho_j\log(\hat \rho_j)+(1-\rho_j)\log(1-\hat \rho_j)\right]$$

其中：$\hat\rho=\frac1k\sum\limits_{i=1}^kh_i$（遍历的是层内的所有输出，$\sum_{j=1}^m$ 则是遍历所有的层））

4. 神经网络中的交叉熵代价函数

为神经网络引入交叉熵代价函数，是为了弥补 sigmoid 型函数的导数形式易发生饱和（saturate，梯度更新的较慢）的缺陷。

首先来看平方误差函数（squared-loss function），对于一个神经元（单输入单输出），定义其代价函数：

$$C=\frac{\left (a-y\right )^2}2$$
其中 $a=\sigma(z),\;z=wx+b$，然后根据对权值（ $w$）和偏置（$b$）的偏导（为说明问题的需要，不妨将 $x=1,\;y=0$）：
$$\frac{\partial\,C}{\partial\,w}=\left(a-y\right)\sigma'(z)x=a\sigma'(z)\\ \frac{\partial\,C}{\partial\,b}=\left(a-y\right)\sigma'(z)=a\sigma'(z)$$

根据偏导计算权值和偏置的更新：

$$w=w-\eta \frac{\partial\,C}{\partial\,w}=w-\eta a\sigma'(z)\\ b=b-\eta \frac{\partial\,C}{\partial\,b}=b-\eta a\sigma'(z)$$

无论如何简化，sigmoid 型函数的导数形式 $\sigma'(z)$ 始终阴魂不散，上文说了 $\sigma'(z)$ 较容易达到饱和，这会严重降低参数更新的效率。

为了解决参数更新效率下降这一问题，我们使用交叉熵代价函数替换传统的平方误差函数。

对于多输入单输出的神经元结构而言，如下图所示：

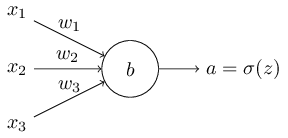
我们将其损失函数定义为：

$$C=-\frac1n\sum_xy\ln a+(1-y)\ln(1-a)$$
其中 $a=\sigma(z),\;z=\sum_jw_jx_j+b$

最终求导得：

$$\frac{\partial\,C}{\partial\,w}=\frac1n\sum_xx_j(\sigma(z)-y)\\ \frac{\partial\,C}{\partial\,b}=\frac1n\sum_x(\sigma(z)-y)$$

就避免了 $\sigma'(z)$ 参与参数更新、影响更新效率的问题；