按之字形顺序打印二叉树
题目描述请实现一个函数按照之字形打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右至左的顺序打印,第三行按照从左到右的顺序打印,其他行以此类推。以题目中的二叉树为例,一步步分析。当二叉树的根结点(结点1)打印之后,它的左子结点(结点2)和右子结点(结点3)先后保存到一个容器中。值得注意的是,在打印第二层的结点时,先打印结点3,后打印结点2。由此可见结点在这个容器中是后进先出的,因此该容
·
题目描述
请实现一个函数按照之字形打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右至左的顺序打印,第三行按照从左到右的顺序打印,其他行以此类推。
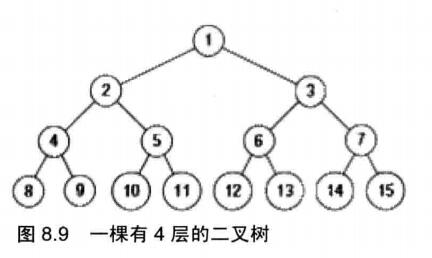
以题目中的二叉树为例,一步步分析。
- 当二叉树的根结点(结点1)打印之后,它的左子结点(结点2)和右子结点(结点3)先后保存到一个容器中。值得注意的是,在打印第二层的结点时,先打印结点3,后打印结点2。由此可见结点在这个容器中是后进先出的,因此该容器可以用栈来实现。
- 接着打印第二层的两个节点。根据题目定义,先打印结点3,再打印结点2,并把他们的子结点放入一个容器中。注意到,打印第三层时,先打印结点2的两个结点,后打印结点3的两个结点。这意味着,我们还可以用一个栈来保存结点2和结点3的子结点。
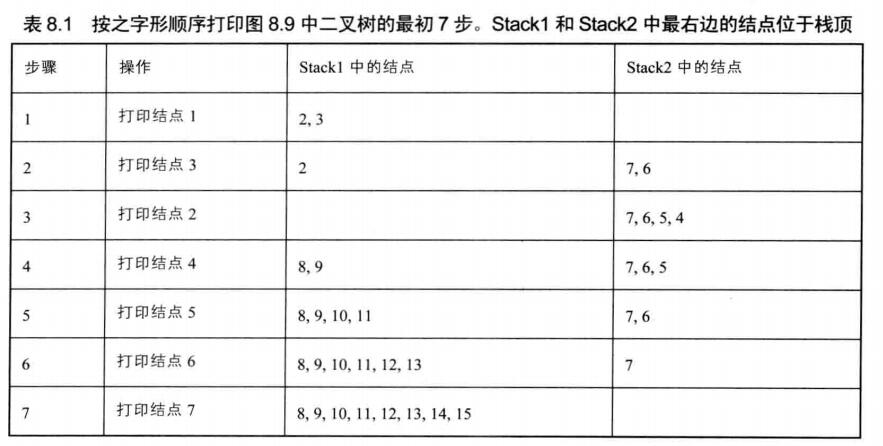
- 此外我们还注意到,第三层的结点是从左向右打印的。按照栈后进先出的特点,应该先保存7到栈中,再保存结点6,之后再分别保存结点5和结点4。也就是说,在打印第二层的时候,我们先保存右子结点到栈中,再保存左子结点到栈中。保存子结点的顺序和打印第一层时不一样。
- 接下来打印第三层。与之前一样,在打印第三层的同时,我们要把第四层的结点保存到一个栈中。由于第四层的打印顺序是从右到左,因此保存的顺序是从左到右。这和保存根结点的两个子结点的顺序是一样的。
从上面的分析可以看出,按之字形顺序打印二叉树,需要两个栈。当我们在打印某一行的结点时,把下一层的结点保存到相应的栈中。如果当前打印的是奇数层,则先保存左子结点再保存右子结点到一个栈中;如果当前打印的是偶数层,则先保存右子结点再保存左子结点到另一个栈中。
vector<vector<int> > Print(TreeNode* pRoot) {
vector<vector<int>> ret;
if(!pRoot)
return ret;
stack<TreeNode*> stacks[2];
int cur = 0;
int next = 1;
stacks[cur].push(pRoot);
vector<int> curVec;
while(!stacks[0].empty() || !stacks[1].empty())
{
TreeNode* pNode= stacks[cur].top();
curVec.push_back(pNode->val);
stacks[cur].pop();
if(cur == 0)
{
if(pNode->left)
stacks[next].push(pNode->left);
if(pNode->right)
stacks[next].push(pNode->right);
}
else
{
if(pNode->right)
stacks[next].push(pNode->right);
if(pNode->left)
stacks[next].push(pNode->left);
}
if(stacks[cur].empty())
{
ret.push_back(curVec);
curVec.clear();
cur = 1-cur;
next = 1-next;
}
}
return ret;
}更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容










所有评论(0)