拉格朗日(lagrange)插值及其MATLAB程序
根据《插值多项式的性质》中的定理6.1可得其中(6.19)称为基函数,(6.18)称为拉格朗日多项式,用(6.18)
·
一、n次拉格朗日插值
根据《插值多项式的性质》中的定理6.1可得
其中(6.19)称为基函数,(6.18)称为拉格朗日多项式,用(6.18)计算插值称为拉格朗日多项式插值。
方法2:通过MATLAB程序计算
>> X = [-2, 0, 1, 2]; Y = [17, 1, 2, 17];
>> p1 = poly(X(1)); p2 = poly(X(2)); p3 = poly(X(3)); p4 = poly(X(4));
>> l01 = conv(conv(p2, p3), p4)/((X(1) - X(2)) * (X(1) - X(3)) * (X(1) - X(4)));
>> l11 = conv(conv(p1, p3), p4)/((X(2) - X(1)) * (X(2) - X(3)) * (X(2) - X(4)));
>> l21 = conv(conv(p1, p2), p4)/((X(3) - X(1)) * (X(3) - X(2)) * (X(3) - X(4)));
>> l31 = conv(conv(p1, p2), p3)/((X(4) - X(1)) * (X(4) - X(2)) * (X(4) - X(3)));
>> l0 = poly2sym(l01), l1 = poly2sym(l11), l2 = poly2sym(l21), l3 = poly2sym(l31)
l0 =
- x^3/24 + x^2/8 - x/12
l1 =
x^3/4 - x^2/4 - x + 1
l2 =
- x^3/3 + (4*x)/3
l3 =
x^3/8 + x^2/8 - x/4
>> P = l01 * Y(1) + l11 * Y(2) + l21 * Y(3) + l31 * Y(4)
P =
1 4 -4 1
>> L = poly2sym(P), x = 0.6; Y = polyval(P, x)
L =
x^3 + 4*x^2 - 4*x + 1
Y =
0.2560
>> syms M; x = 0.6;
>> R3 = M * abs((x - X(1)) * (x - X(2)) * (x - X(3)) * (x - X(4))) / 24
R3 =
(91*M)/2500
>> 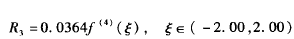
二、拉格朗日多项式和基函数的MATLAB程序
编辑M文件:
%lagran1.m
%求拉格朗日插值多项式和基函数
%输入的量:n+1个节点(x_i,y_i)(i = 1,2, ... , n+1)横坐标向量X,纵坐标向量Y
%输出的量:n次拉格朗日插值多项式L及其系数向量C,基函数l及其系数矩阵L
function [C,L,L1,l] = lagran1(X,Y)
m = length(X); L = ones(m,m);
for k = 1 : m
V = 1;
for i = 1 : m
if k ~= i
V = conv(V,poly(X(i))) / (X(k) - X(i));
end
end
L1(k, :) = V; l(k, :) = poly2sym(V);
end
C = Y * L1;
L = Y * l;
>> X = [-2.15 -1.00 0.01 1.02 2.03 3.25];
>> Y = [17.03 7.24 1.05 2.03 17.06 23.05];
>> [C,L,L1,l] = lagran1(X,Y);
>> C
C =
-0.2169 0.0648 2.1076 3.3960 -4.5745 1.0954
>> vpa(L,5)
ans =
- 0.21686*x^5 + 0.06482*x^4 + 2.1076*x^3 + 3.396*x^2 - 4.5745*x + 1.0954
>> L1
L1 =
-0.0056 0.0299 -0.0323 -0.0292 0.0382 -0.0004
0.0331 -0.1377 -0.0503 0.6305 -0.4852 0.0048
-0.0693 0.2184 0.3961 -1.2116 -0.3166 1.0033
0.0687 -0.1469 -0.5398 0.6528 0.9673 -0.0097
-0.0317 0.0358 0.2530 -0.0426 -0.2257 0.0023
0.0049 0.0004 -0.0266 0.0001 0.0220 -0.0002
>> vpa(l,5)
ans =
- 0.0056263*x^5 + 0.029875*x^4 - 0.032273*x^3 - 0.029239*x^2 + 0.038157*x - 0.00037862
0.033098*x^5 - 0.13769*x^4 - 0.050322*x^3 + 0.63051*x^2 - 0.48517*x + 0.0047887
- 0.069344*x^5 + 0.21843*x^4 + 0.39608*x^3 - 1.2116*x^2 - 0.31662*x + 1.0033
0.06865*x^5 - 0.14691*x^4 - 0.53981*x^3 + 0.65279*x^2 + 0.9673*x - 0.0097378
- 0.031721*x^5 + 0.035845*x^4 + 0.25295*x^3 - 0.042557*x^2 - 0.22568*x + 0.0022608
0.0049432*x^5 + 0.00044489*x^4 - 0.026633*x^3 + 0.000092729*x^2 + 0.022008*x - 0.00022006三、拉格朗日插值及其误差估计的MATLAB程序
编写M文件
%lagrane.m
%拉格朗日插值及其误差估计
%输入的量:X是n+1个节点(x_i,y_i)(i = 1,2, ... , n+1)横坐标向量,Y是纵坐标向量,
%x是以向量形式输入的m个插值点,M在[a,b]上满足|f~(n+1)(x)|≤M
%注:f~(n+1)(x)表示f(x)的n+1阶导数
%输出的量:y为m个插值构成的向量,R是误差限
function [y, R] = lagrange(X, Y, x, M)
n = length(X);m = length(x);
for i = 1:m
z = x(i);
s = 0.0;
for k = 1:n
p = 1.0; q1 = 1.0; c1 = 1.0;
for j = 1:n
if j~=k
p = p * (z - X(j)) / (X(k) - X(j));
end
q1 = abs(q1 * (z - X(j)));
c1 = c1 * j;
end
s = p * Y(k) + s;
end
y(i) = s;
R(i) = M * q1 / c1;
end
例:用Lagrange插值来求sinx在某点的值,并估计其误差,已知sin0° = 0, sin30° = 0.5, sin45° = 0.7071, sin60° = 0.8660, sin90° = 1.
X 0 pi/6 pi/4 pi/3 pi/2
Y 0 0.5 0.7071 0.8660 1
解:
>> X = [0 pi/6 pi/4 pi/3 pi/2];
>> Y = [0 0.5 0.7071 0.8660 1];
>> x = linspace(0,pi,50);
>> M = 1;
>> [y, R] = lagrange(X, Y, x, M);
>> y1 = sin(x);
>> errorbar(x,y,R,'.g')
>> hold on
>> plot(X, Y, 'or', x, y, '.k', x, y1, '-b');
>> legend('误差','样本点','拉格朗日插值估算','sin(x)');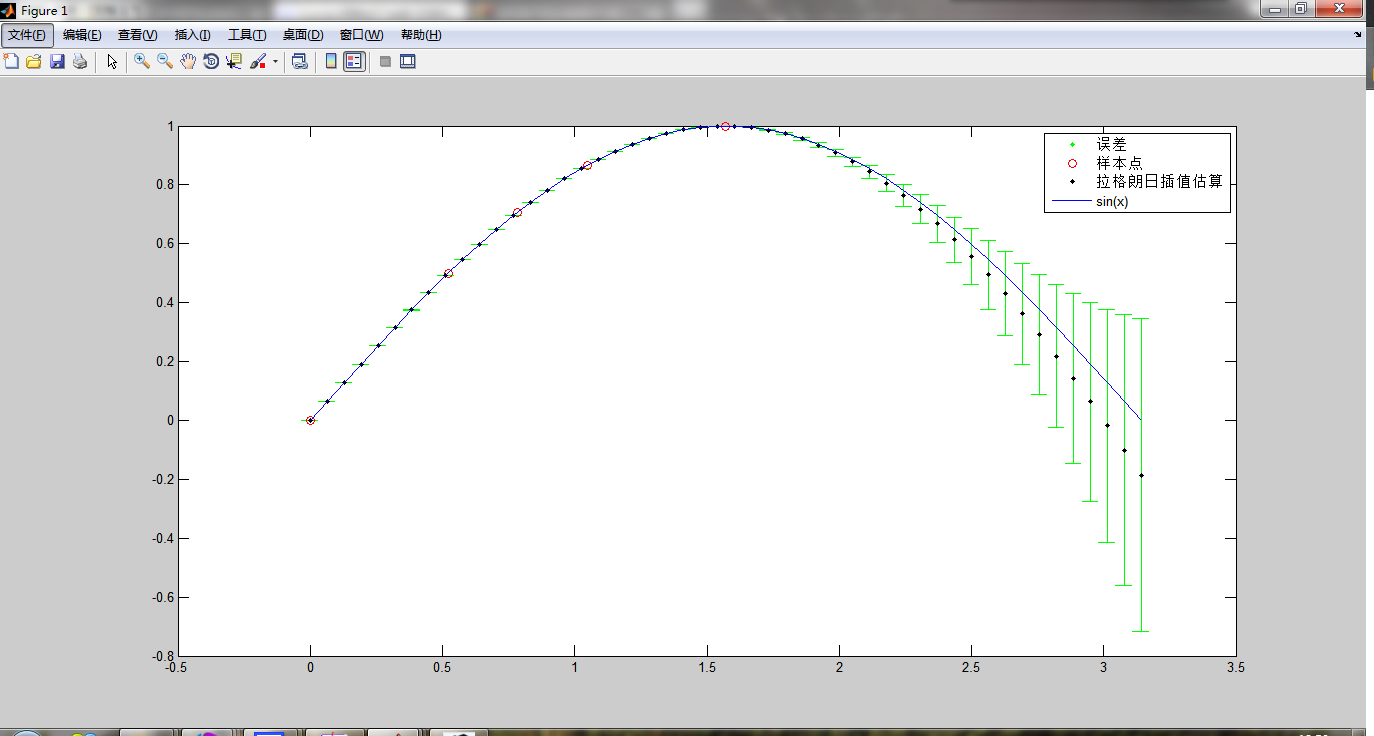
更多推荐
 已为社区贡献17条内容
已为社区贡献17条内容













所有评论(0)