红黑树由于节点颜色的特性，保证其是一种自平衡的二叉搜索树。

红黑树的一系列规则虽然实现起来比较复杂，但是遵循起来却比较简单，而且红黑树的插入，删除性能也还不错。

所以红黑树在内核中的应用非常广泛，掌握好红黑树，即有利于阅读内核源码，也可以在自己的代码中借鉴这种数据结构。

红黑树必须满足的规则：

• 所有节点都有颜色，要么红色，要么黑色
• 根节点是黑色，所有叶子节点也是黑色
• 叶子节点中不包含数据
• 非叶子节点都有2个子节点
• 如果一个节点是红色，那么它的父节点和子节点都是黑色的
• 从任何一个节点开始，到其下叶子节点的路径中都包含相同树木的黑节点

红黑树中最长的路径就是红黑交替的路径，最短的路径是全黑节点的路径，再加上根节点和叶子节点都是黑色，

从而可以保证红黑树中最长路径的长度不会超过最短路径的2倍。

一、相关文件在内核中的位置

内核中关于红黑树定义的头文件位于：<linux/rbtree.h> include/linux/rbtree.h

头文件中定义的函数的实现位于：lib/rbtree.c

内核中红黑树的使用和链表(list)有些类似，是将红黑树的节点放入自定义的数据结构中来使用的。

首先需要注意的一点是红黑树节点的定义：

struct rb_node
{
    unsigned long  rb_parent_color;
#define    RB_RED        0
#define    RB_BLACK    1
    struct rb_node *rb_right;
    struct rb_node *rb_left;
} __attribute__((aligned(sizeof(long))));

刚开始看到这个定义的时候，我觉得很奇怪，等到看懂了之后，才知道原来作者巧妙的利用内存对齐来将2个内容存入到一个字段中（不服不行啊^_^!）。

字段 rb_parent_color 中保存了2个信息：

1. 父节点的地址
2. 本节点的颜色

这2个信息是如何存入一个字段的呢？主要在于 __attribute__((aligned(sizeof(long))));

这行代码的意思就是 struct rb_node 在内存中的地址需要按照4 bytes或者8 bytes对齐。

注：sizeof(long) 在32bit系统中是4 bytes，在64bit系统中是8 bytes

 

struct rb_node的地址按4 bytes对齐，意味着分配的地址都是4的倍数。

4 的二进制为 100 ，所以申请分配的 struct rb_node 的地址的最后2位始终是零，

struct rb_node 的字段 rb_parent_color 就是利用最后一位来保存节点的颜色信息的。

（有时候不禁就想感慨一下，太巧妙了！！太精妙了！！）

/* rb_parent_color 保存了父节点的地址和本节点的颜色 */

/* 将 rb_parent_color 的最后2位置成0，即将颜色信息去掉，剩下的就是parent节点的地址 */
#define rb_parent(r)   ((struct rb_node *)((r)->rb_parent_color & ~3))

/* 取得 rb_parent_color 二进制表示的最后一位，即用于保存颜色信息的那一位 */
#define rb_color(r)   ((r)->rb_parent_color & 1)

/* 将 rb_parent_color 二进制表示的最后一位置为0，即置为红色 */
#define rb_set_red(r)  do { (r)->rb_parent_color &= ~1; } while (0)

/* 将 rb_parent_color 二进制表示的最后一位置为1，即置为黑色 */
#define rb_set_black(r)  do { (r)->rb_parent_color |= 1; } while (0)

在刚开始看的时候就没怎么想明白这个事，明白了4字节对齐的问题再看上面的头文件就比较轻松了！

还有需要重点看的就是rb_tree.c中的5个函数，下面对这5个函数进行一些注释：

二、函数介绍

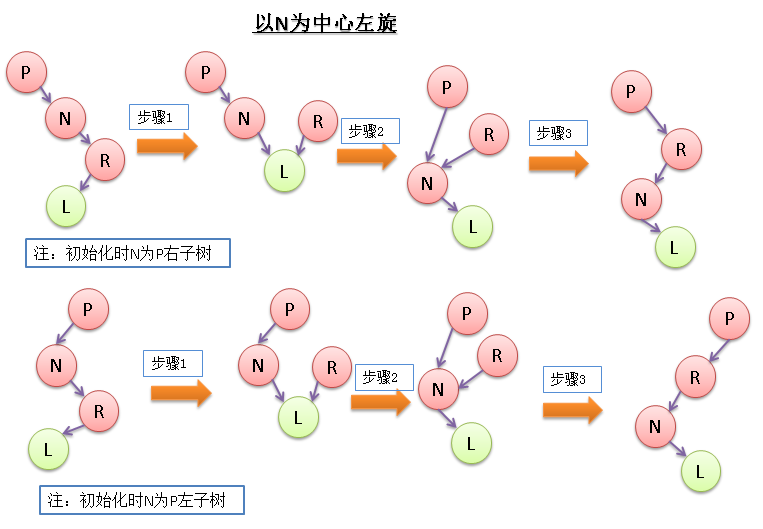
函数1：左旋操作，当右子树的长度过大导致树不平衡时，进行左旋操作：

/*
 *  左旋操作其实就3个动作：见图left
 *  1. node的右子树关联到right的左子树
 *  2. right的左子树关联到node
 *  3. right取代node的位置
 *  其他带代码都是一些相应的parent指针的变化
 */
static void __rb_rotate_left(struct rb_node *node, struct rb_root *root)
{
    /* 初始化相对于node节点的父节点(图中的P)和右节点(图中的R) */
    struct rb_node *right = node->rb_right;
    struct rb_node *parent = rb_parent(node);

    /* 步骤1  */
    if ((node->rb_right = right->rb_left))
        rb_set_parent(right->rb_left, node);

    /* 步骤2 */
    right->rb_left = node;
    rb_set_parent(right, parent);

    /* node的parent NOT NULL 时，right取代原先的node的位置 */
    if (parent)
    {
        if (node == parent->rb_left)
            parent->rb_left = right;
        else
            parent->rb_right = right;
    }

    /* node的parent NULL 时，说明node原先时root节点，将新的root指向root即可 */
    else
        root->rb_node = right;
    rb_set_parent(node, right);
}

左旋操作图解:

函数2：右旋操作，和左旋操作类似。

 

函数3：追加节点后，设置此节点的颜色。

/*
 *  本函数没有插入节点的功能，只是在插入新节点后，设置新节点的颜色，从而保证红黑树的平衡性。
 *  新插入的节点默认都是红色的。
 *  
 *  下面的代码看着复杂，其实只要时时记住红黑树的几个重要特性，就会发现下面的都是在尽量保持住红黑树的这些特性。
 *  1. 无论从哪个节点开始，到其叶子节点的路径中包含的黑色节点个数时一样的
 *  2. 不能有连续的2个红色节点，即父节点和子节点不能同时为红色
 *  所以最简单的情况就是：插入节点的父节点是黑色的。那么插入一个红节点后不会有任何影响。
 *  3. 左旋操作有减少右子树高度的作用
 *  4. 同理，右旋操作有减少左子树高度的作用
 */
void rb_insert_color(struct rb_node *node, struct rb_root *root)
{
    struct rb_node *parent, *gparent;

    while ((parent = rb_parent(node)) && rb_is_red(parent))
    {
        gparent = rb_parent(parent);

        /* parent 是 gparent的左子树时 */
        if (parent == gparent->rb_left)
        {
            {
                /* gparent的左右子树的黑色节点都增加一个，仍然平衡 */
                register struct rb_node *uncle = gparent->rb_right;
                if (uncle && rb_is_red(uncle))
                {
                    rb_set_black(uncle);
                    rb_set_black(parent);
                    rb_set_red(gparent);
                    node = gparent;
                    continue;
                }
            }

            /* node为parent右子树时 */
            if (parent->rb_right == node)
            {
                register struct rb_node *tmp;
                /* 左旋后，parent的位置被node取代，然后再交换parent和node的位置，
                 * 相当于node是parent的左子树
                 * 由于node和parent都是红色（否则到不了这一步），parent左右子树的黑色节点数仍然是相等的
                 */
                __rb_rotate_left(parent, root);
                tmp = parent;
                parent = node;
                node = tmp;
            }

            /* parent 红->黑，gparent左子树比右子树多一个黑色节点
             * 右旋后，gparent左子树高度减一，减少的节点即parent，减少了一个黑色节点，parent变为新的gparent。
             * 所以右旋后，新的gparent的左右子树的黑色节点数再次平衡了
             */
            rb_set_black(parent);
            rb_set_red(gparent);
            __rb_rotate_right(gparent, root);
        /* parent 是 gparent的右子树时，和上面的过程类似 */
        } else {
            {
                register struct rb_node *uncle = gparent->rb_left;
                if (uncle && rb_is_red(uncle))
                {
                    rb_set_black(uncle);
                    rb_set_black(parent);
                    rb_set_red(gparent);
                    node = gparent;
                    continue;
                }
            }

            if (parent->rb_left == node)
            {
                register struct rb_node *tmp;
                __rb_rotate_right(parent, root);
                tmp = parent;
                parent = node;
                node = tmp;
            }

            rb_set_black(parent);
            rb_set_red(gparent);
            __rb_rotate_left(gparent, root);
        }
    }

    rb_set_black(root->rb_node);
}

函数4：删除一个节点，并且调整删除后各节点的颜色。其中调整节点颜色其实是另一个单独的函数。

/* 删除节点时，如果被删除的节点左子树==NULL或右子树==NULL或左右子树都==NULL
 * 那么只要把被删除节点的左子树或右子树直接关联到被删节点的父节点上即可，剩下的就是调整各节点颜色。
 * 只有被删节点是黑色才需要调整颜色，因为删除红色节点不影响红黑树的特性。
 *
 * 被删节点左右子树都存在的情况下，其实就是用中序遍历中被删节点的下一个节点来替代被删节点。
 * 代码中的操作只是将各个指针指向新的位置而已。
 */
void rb_erase(struct rb_node *node, struct rb_root *root)
{
    struct rb_node *child, *parent;
    int color;

    if (!node->rb_left)
        child = node->rb_right;
    else if (!node->rb_right)
        child = node->rb_left;
    else
    {
        struct rb_node *old = node, *left;

        /* 寻找中序遍历中被删节点的下一个节点 */
        node = node->rb_right;
        while ((left = node->rb_left) != NULL)
            node = left;

        /* 替换要删除的节点old */
        if (rb_parent(old)) {
            if (rb_parent(old)->rb_left == old)
                rb_parent(old)->rb_left = node;
            else
                rb_parent(old)->rb_right = node;
        } else
            root->rb_node = node;

        child = node->rb_right;
        parent = rb_parent(node);
        color = rb_color(node);

        if (parent == old) {
            parent = node;
        } else {
            if (child)
                rb_set_parent(child, parent);
            parent->rb_left = child;

            node->rb_right = old->rb_right;
            rb_set_parent(old->rb_right, node);
        }

        node->rb_parent_color = old->rb_parent_color;
        node->rb_left = old->rb_left;
        rb_set_parent(old->rb_left, node);

        goto color;
    }

    parent = rb_parent(node);
    color = rb_color(node);

    if (child)
        rb_set_parent(child, parent);
    if (parent)
    {
        if (parent->rb_left == node)
            parent->rb_left = child;
        else
            parent->rb_right = child;
    }
    else
        root->rb_node = child;

 color:
    if (color == RB_BLACK)
        __rb_erase_color(child, parent, root);
}

函数5：删除一个黑色节点后，重新调整相关节点的颜色。

/* 这里的node就是上面函数中的child，所有node节点的左右子树肯定都是NULL
 * 不满足红黑树规则的就是从parent节点开始的子树，只要给从parent开始的子树增加一个黑色节点就行
 * 如果从parent节点开始的节点全是黑色，node和parent都继续向上移动
 */
static void __rb_erase_color(struct rb_node *node, struct rb_node *parent,
                 struct rb_root *root)
{
    struct rb_node *other;

    /* （node不为NULL 且 node是黑色的） 或者 node == NULL */
    while ((!node || rb_is_black(node)) && node != root->rb_node)
    {
        if (parent->rb_left == node)
        {
            other = parent->rb_right;
            if (rb_is_red(other))
            {
                rb_set_black(other);
                rb_set_red(parent);
                __rb_rotate_left(parent, root);
                other = parent->rb_right;
            }
            /* 如果从parent节点开始的节点全是黑色，node和parent都继续向上移动 */
            if ((!other->rb_left || rb_is_black(other->rb_left)) &&
                (!other->rb_right || rb_is_black(other->rb_right)))
            {
                rb_set_red(other);
                node = parent;
                parent = rb_parent(node);
            }
            else
            {
                if (!other->rb_right || rb_is_black(other->rb_right))
                {
                    rb_set_black(other->rb_left);
                    rb_set_red(other);
                    __rb_rotate_right(other, root);
                    other = parent->rb_right;
                }
                rb_set_color(other, rb_color(parent));
                rb_set_black(parent);
                rb_set_black(other->rb_right);
                __rb_rotate_left(parent, root);
                node = root->rb_node;
                break;
            }
        }
        else
        {
            other = parent->rb_left;
            if (rb_is_red(other))
            {
                rb_set_black(other);
                rb_set_red(parent);
                __rb_rotate_right(parent, root);
                other = parent->rb_left;
            }
            if ((!other->rb_left || rb_is_black(other->rb_left)) &&
                (!other->rb_right || rb_is_black(other->rb_right)))
            {
                rb_set_red(other);
                node = parent;
                parent = rb_parent(node);
            }
            else
            {
                if (!other->rb_left || rb_is_black(other->rb_left))
                {
                    rb_set_black(other->rb_right);
                    rb_set_red(other);
                    __rb_rotate_left(other, root);
                    other = parent->rb_left;
                }
                rb_set_color(other, rb_color(parent));
                rb_set_black(parent);
                rb_set_black(other->rb_left);
                __rb_rotate_right(parent, root);
                node = root->rb_node;
                break;
            }
        }
    }
    if (node)
        rb_set_black(node);
}

这是别人关于linux内核中红黑树的分析，接下来还有自己的理解，未完待续！