有很多小伙伴在后台私信我说对于代码很模糊，看不懂我发的博客代码，一些大模型功能的实现觉得很困难，代码能力的薄弱确实让我们在热爱的领域进步举步维艰，所以我准备出几期基础的算法教学，帮助大家学习。

当然如果你的目标是去大厂工作，这个可能只能做个基础，最重要还是得刷刷力扣，虽然算法在AI时代弱化了很多，但是我们也要有个基本的概念。

如果你的目标和我一样，不是为了工作，单纯对这个方向感兴趣，作为一个爱好，那么这个系列的博客完全足够了。

本博客主要讲解krahets大佬的算法课程。

首先申明，这个课程非常基础，完全面向初学者，已经懂算法的可以不用看！！！

1.数据结构分类：

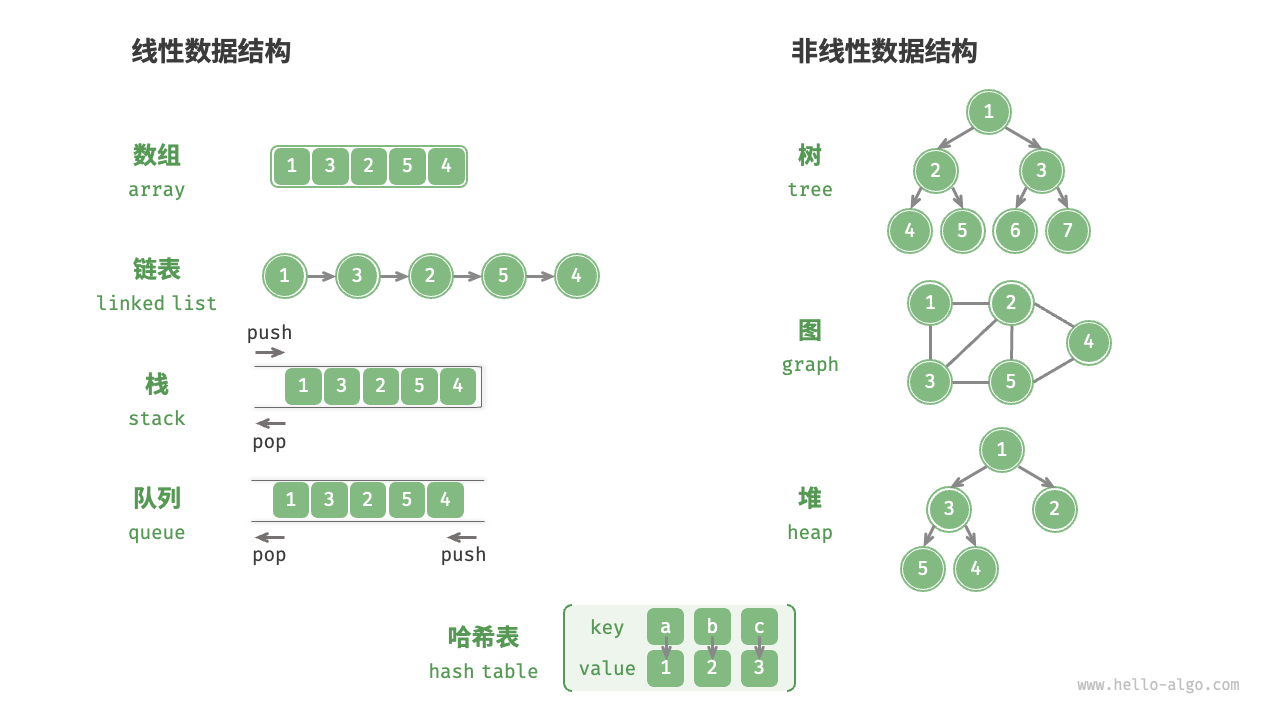
常见的数据结构包括数组、链表、栈、队列、哈希表、树、堆、图，它们可以从“逻辑结构”和“物理结构”两个维度进行分类。

A. 逻辑结构 (Logical Structure)

逻辑结构这是指数据之间逻辑上的关系，不管在电脑里具体怎么存，它们看起来是什么样的。

  • 线性结构 (Linear): 数据像一条线一样排队。

    • 例子：数组 (Array)、链表 (Linked List)、栈 (Stack)、队列 (Queue)。

  • 非线性结构 (Non-linear): 数据之间关系复杂，不是一对一。

    • 树 (Tree): 一对多（像家谱、文件系统）。

    • 图 (Graph): 多对多（像社交网络、地图导航）。

这里引用一张图：

B. 物理结构 (Physical Structure)

这是指数据真正在内存条里是如何存放的。这是决定性能的关键。

  • 连续空间 (Contiguous): 数据挤在一起，紧挨着存放。

    • 代表： 数组 (Array)。

    • 优点： 查找快（因为地址连续，可以直接计算偏移量），对 CPU 缓存友好。

    • 缺点： 插入和删除慢（因为要移动后面的所有元素），大小固定（扩容麻烦）。

  • 分散空间 (Linked): 数据零散地分布在内存各处，通过“指针”（像线一样）连起来。

    • 代表： 链表 (Linked List)。

    • 优点： 插入删除快（改个指针就行），大小动态灵活。

    • 缺点： 查找慢（必须从头顺藤摸瓜），占用额外空间存指针。

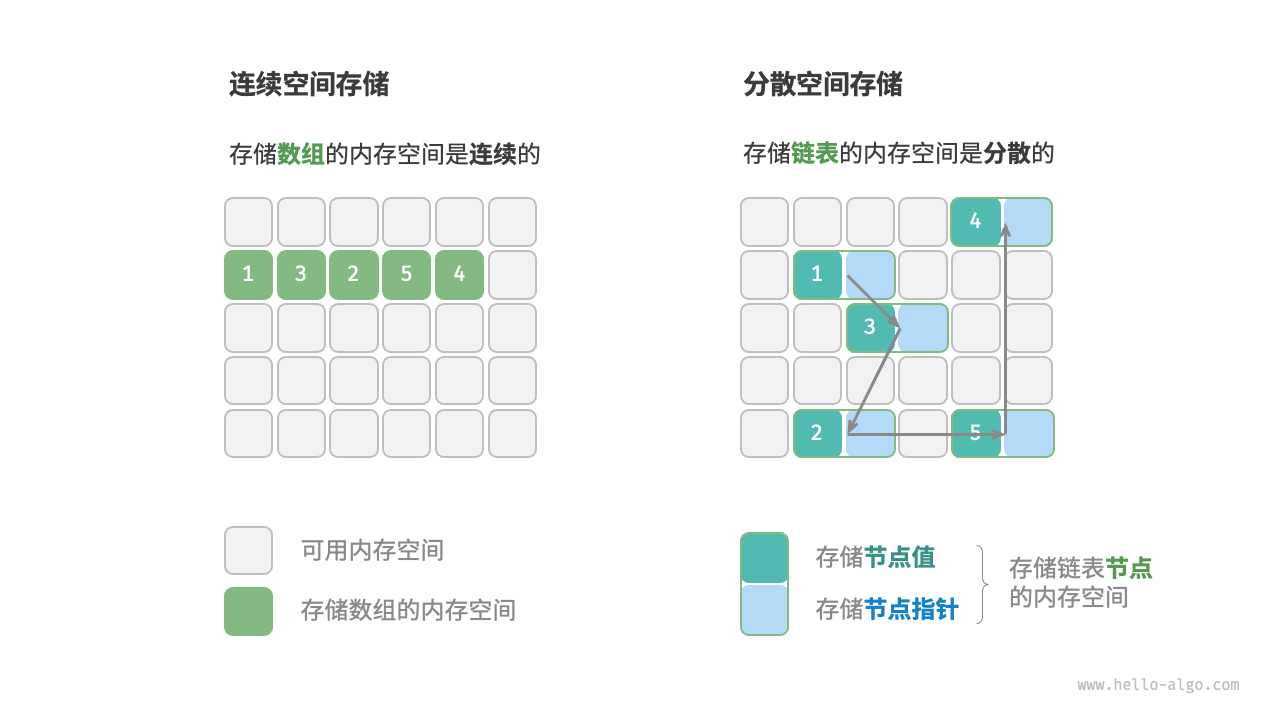
链表在初始化后，仍可以在程序运行过程中对其长度进行调整，因此也称“动态数据结构”。数组在初始化后长度不可变，因此也称“静态数据结构”。值得注意的是，数组可通过重新分配内存实现长度变化，从而具备一定的“动态性”。

有个比较特殊的数据结构，哈希表：

它是数据结构里的“速度之王”。如果说数组是“排队”，哈希表就是“传送门”。

假设你是一个老师，你想找某位同学的试卷。

  • 数组/链表模式（遍历）：

    你拿着名字，从第一张卷子开始翻：“是张三吗？不是。是李四吗？不是。是王五吗？……找到了。”

    • 耗时： O(n)，人越多越慢。

  • 哈希表模式（映射）：

    你有一个神奇的计算器（哈希函数）。你输入名字“王五”，计算器直接显示：“在第 8 排第 3 个柜子”。你走过去直接拿，不用翻看其他任何卷子。

    • 耗时： O(1)，无论全校有多少人，你都是一次拿对。

哈希表由三个主要部分组成：

  1. Key (键)： 你用来查找的东西（比如 "name": "zhangsan"）。

  2. Hash Function (哈希函数)： 这是一个数学公式。它的作用是把任意长度的输入（Key），变成一个固定的数字（索引）。

    • 比如：Hash("zhangsan") = 352

    • 比如：Hash("lisi") = 901

  3. Buckets (桶/数组)： 实际存数据的地方。哈希函数算出的数字，就是数据在数组里的下标。

过程演示：

存数据：

你想存 {"apple": 5元}。

  1. 哈希函数计算 "apple" $\rightarrow$ 得到索引 02。

  2. 把 5元 扔进数组下标为 02 的格子里。

取数据：

你想找 "apple" 多少钱。

  1. 哈希函数再次计算 "apple" $\rightarrow$得到索引 02。

  2. 直接去下标 02 拿数据。不需要遍历！

虽然哈希函数很厉害，但内存是有限的。万一遇到这种情况怎么办？

  • Hash("apple") = 02

  • Hash("banana") = 02

两个不同的 Key 算出了同一个房间号！这就叫哈希冲突。

怎么解决？

最经典的方法叫拉链法 (Chaining)：

就像如果两个人被分到了同一个单人宿舍，那就把单人床改成“上下铺”（链表）。

  • 在下标 02 的位置，不是直接存一个数，而是挂一个链表。

  • 里面先存了 apple，后面再挂一个 banana。

  • 查找时，先定位到 02，然后顺着链表找一下是 apple 还是 banana。

2.基本数据类型;

当谈及计算机中的数据时，我们会想到文本、图片、视频、语音、3D 模型等各种形式。尽管这些数据的组织形式各异，但它们都由各种基本数据类型构成。

基本数据类型是 CPU 可以直接进行运算的类型，在算法中直接被使用，主要包括以下几种。

第一层面：Python 的 5 大基本数据类型

整数 (Integer, int)

  • 也就是： 没有小数点的数字。

  • 特点： 在 Python 中，int 是无限精度的（只要内存够，多大都能存）。不像 C++ 或 Java 有 int / long 之分

浮点数 (Float, float)

  • 也就是： 带小数点的数字（科学计数法也算）。

  • 特点： Python 的 float 实际上是 C 语言中的 双精度浮点数 (Double, 64-bit)。

布尔值 (Boolean, bool)

  • 也就是： 真 (True) 或 假 (False)。其实它在底层就是 1 和 0。

字符串 (String, str)

  • 也就是： 文本。

空值 (NoneType, None)

  • 也就是： 什么都没有。

第二层面：深度学习必须懂的“底层类型”

只知道 Python 的 int 和 float 是不够的。因为在 PyTorch/TensorFlow 中，为了节省显存（VRAM）和加速计算，我们对数据类型极其敏感。

在 numpy 或 torch.Tensor 中，基本类型被划分得更细：

这是你训练大模型时最关心的。

  • float32 (FP32, 单精度): 深度学习的默认标准。

  • float16 (FP16, 半精度): 显存占用减半，训练速度翻倍。混合精度训练（Mixed Precision）的核心。

  • bfloat16 (BF16): Google 搞出来的，专门为 AI 设计。为了在大模型训练中防止溢出，牺牲了精度，保留了指数位。现在的大模型（如 LLaMA）基本都在用这个。

  • float64 (FP64, Double): Python 原生 float 的默认精度。但在深度学习中极少使用，因为太占显存且计算慢。

整数的位数

  • int64 (Long): PyTorch 中 Embedding 层查找 Token ID 时，通常要求索引是 int64（或者 LongTensor）。

  • int8 (Byte): 量化（Quantization）时会用到。把大模型参数从 float 压成 int8，模型体积直接缩小 4 倍，甚至可以在手机上跑。

基本数据类型以二进制的形式存储在计算机中。一个二进制位即为 1比特。在绝大多数现代操作系统中， 1字节（byte）由  8比特（bit）组成。

基本数据类型的取值范围取决于其占用的空间大小。

类型 (Type) 占用空间 取值范围 典型应用场景
int8 1 Byte -128 ~ 127 模型量化 (Quantization)
uint8 1 Byte 0 ~ 255 图像像素 (RGB 值)
int16 2 Bytes -32,768 ~ 32,767 音频处理
int32 4 Bytes 约 -21亿 ~ 21亿 某些索引
int64 (Long) 8 Bytes 极大 (约 $\pm 9 \times 10^{18}$) PyTorch 默认索引类型
类型 (Type) 占用空间 取值范围 (Approx) 精度 (有效位数) 典型应用场景
float16 (FP16) 2 Bytes $\pm 6.5 \times 10^4$ ~3-4 位 混合精度训练
bfloat16 2 Bytes $\pm 3.4 \times 10^{38}$ ~2-3 位 大模型 (LLaMA等)
float32 (FP32) 4 Bytes $\pm 3.4 \times 10^{38}$ ~7 位 深度学习标准精度
float64 (Double) 8 Bytes $\pm 1.8 \times 10^{308}$ ~15-17 位 科学计算 (非AI)

那么，基本数据类型与数据结构之间有什么联系呢？我们知道，数据结构是在计算机中组织与存储数据的方式。这句话的主语是“结构”而非“数据”。

如果想表示“一排数字”，我们自然会想到使用数组。这是因为数组的线性结构可以表示数字的相邻关系和顺序关系，但至于存储的内容是整数 int、小数 float 还是字符 char ，则与“数据结构”无关。

换句话说，基本数据类型提供了数据的“内容类型”，而数据结构提供了数据的“组织方式”。

3.数字编码

在上一节的表格中我们发现，所有整数类型能够表示的负数都比正数多一个，例如 int8的取值范围是 -128 ~ 127 。这个现象比较反直觉，它的内在原因涉及原码、反码、补码的相关知识。

在计算机眼里，没有数字，只有开关（0 和 1）。 所谓的“数字编码”，就是如何制定一套规则，把现实世界的数学（整数、小数、负数）翻译成 0 和 1 的排列组合。

主要分为两大块：整数编码（补码系统） 和 浮点数编码（IEEE 754标准）。

这个就是一个扩展阅读，不上王者不用学，甚至我认为作为教材这个都有点多余了，只要知道这个大概的概念就行了

第一部分：整数编码 (Integer)

1. 正整数：原码 (Sign-Magnitude)

这是最符合人类直觉的。

  • 假设我们需要 4 位二进制（4-bit）。

  • 数字 5 对应0101

  • 数字 2 对应 0010

  • 很简单，直接转二进制。

2. 负数的难题

如果要表示 负数（如 -5），怎么办？

  • 直觉想法（原码）： 用第一位（最高位）当符号位。0 是正，1 是负。

    • +5 = 0101

    • -5 = 1101

  • 这就出大问题了：

    1. 两个零： 会出现 0000 (+0) 和 1000 (-0)。这就浪费了一个编码，而且逻辑判断麻烦。

    2. 数学运算无法统一： 计算机希望只设计“加法器”，不设计“减法器”（为了省电路）。

      • 如果用原码算 1 + (-1)：

      • 0001 + 1001 = 1010 (-2)。结果错了！

3. 完美的解决方案：补码 (Two's Complement)

现代计算机（包括 Python 底层、PyTorch 的 int）全都使用补码。

规则：

  • 正数： 保持不变。

  • 负数： 取反（0变1，1变0），然后加 1。

为什么这样设计？（核心原理：时钟理论）

想象一个只有 12 小时的时钟。

  • 现在的指针是 2 点。

  • 你想让指针倒退 1 小时（做减法：$2 - 1$）。

  • 方法一： 逆时针拨 1 格 $\rightarrow$ 1 点。

  • 方法二： 顺时针拨 11 格 $\rightarrow$ 也是 1 点

补码就是那个“顺时针拨 11 格”。 它把“减法”变成了“加法”（加上一个很大的数，利用溢出回到正确位置）。

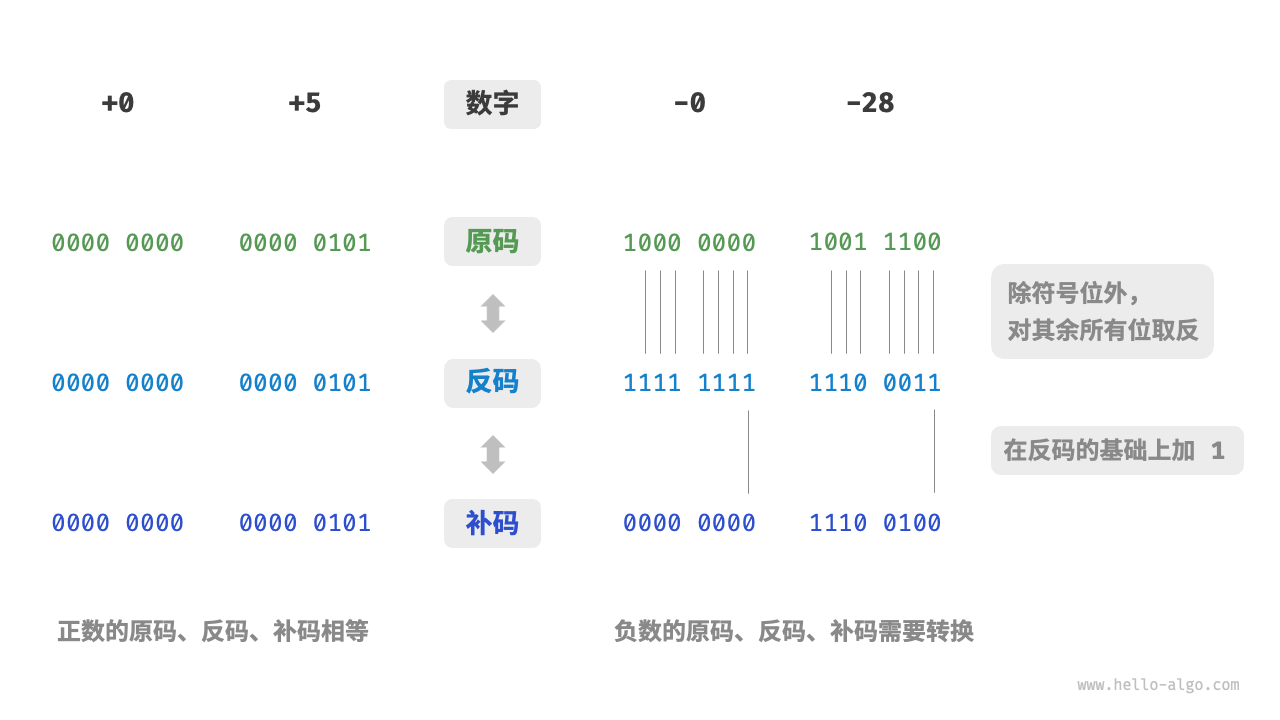
例子：计算 1 + (-1) (4-bit 系统)

  1. +1 的补码 0001

  2. -1 的补码原码 1001  反码 1110  加1  1111

  3. 相加：

    $\begin{array}{r} 0001 \\ + 1111 \\ \hline 10000 \end{array}$

  4. 因为只有 4 位，最高位的 1 溢出丢弃，结果变成 0000 (即 0)。结果正确！

启示： 这就是为什么 int8 的范围是 -128 到 127。因为 10000000 被规定为 -128，而没有对应的正数 +128。

第二部分：浮点数编码 (Float - IEEE 754)

计算机存小数，用的是 “科学计数法” 的二进制版。

公式：$V = (-1)^S \times M \times 2^E$

它把 32 个比特位（以 float32 为例）切成了三段：

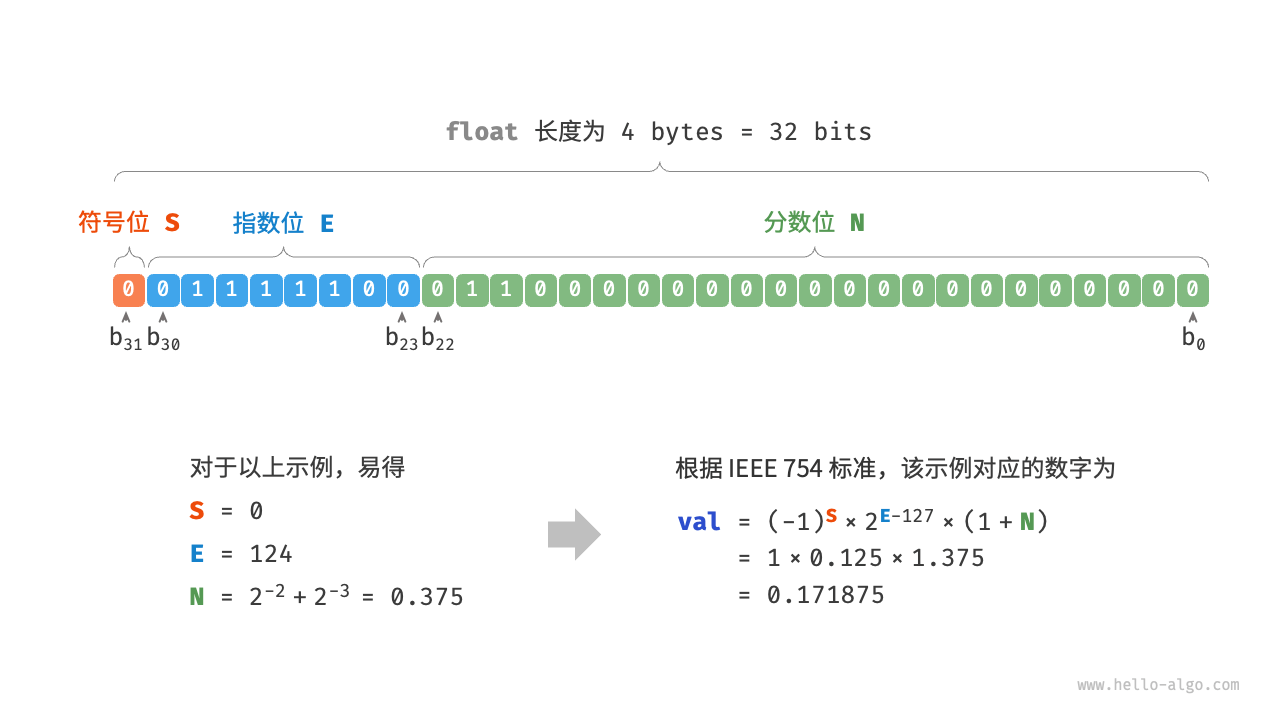
1. 符号位 (Sign, S) - 1 bit

  • 0 代表正，1 代表负。

2. 指数位 (Exponent, E) - 8 bits

  • 决定了数字的 大小范围（Range）。

  • 相当于科学计数法 $1.23 \times 10^5$ 里的那个 5。

  • 指数位越多，能表示的数就越大（比如能到 $10^{38}$ 还是 $10^{308}$）。

3. 尾数位 (Mantissa / Fraction, M) - 23 bits

  • 决定了数字的 精度（Precision）。

  • 相当于科学计数法 1.23456...里的 23456。

  • 尾数位越多，小数点后面的数字越精确。

为了彻底理解“编码只是解释方式”，请看下面这串 32 位的二进制：

0011 1111 1000 0000 0000 0000 0000 0000

  • 如果你告诉 CPU “这是个整数 (int32)”： CPU 会按补码读，结果是 1,065,353,216。

  • 如果你告诉 CPU “这是个浮点数 (float32)”： CPU 会按 IEEE 754 读（符号0，指数127，尾数0），结果是 1.0。

结论：数据结构定义了内存的布局，而数据类型（编码）定义了如何理解这块内存。

4.字符编码

这个就太熟悉了，我们深度学习基本都会，但是我还是讲一下吧，毕竟有很多交叉学科的同学可能没有接触过

在计算机中，所有数据都是以二进制数的形式存储的，字符 char 也不例外。为了表示字符，我们需要建立一套“字符集”，规定每个字符和二进制数之间的一一对应关系。有了字符集之后，计算机就可以通过查表完成二进制数到字符的转换。

ASCII 码是最早出现的字符集，其全称为 American Standard Code for Information Interchange（美国标准信息交换代码）。它使用 7 位二进制数（一个字节的低 7 位）表示一个字符，最多能够表示 128 个不同的字符。如图 3-6 所示，ASCII 码包括英文字母的大小写、数字 0 ~ 9、一些标点符号，以及一些控制字符（如换行符和制表符）。

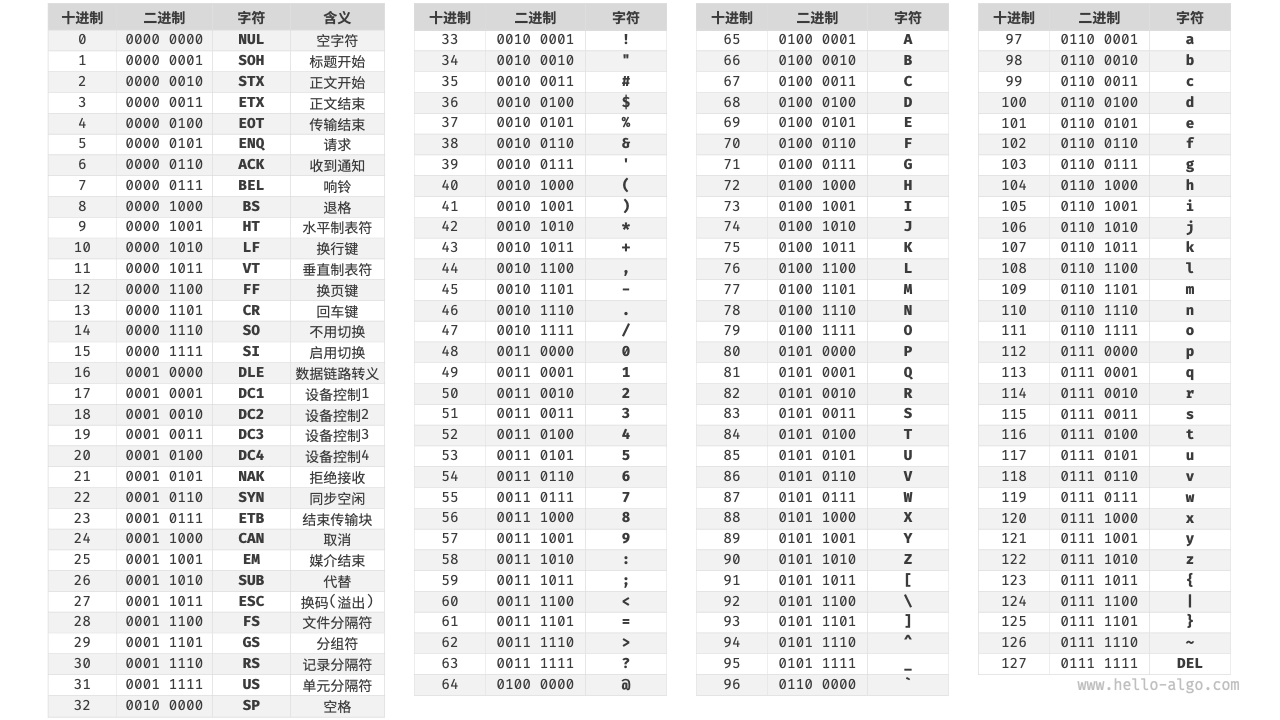
然而，ASCII 码仅能够表示英文。随着计算机的全球化，诞生了一种能够表示更多语言的 EASCII 字符集。它在 ASCII 的 7 位基础上扩展到 8 位，能够表示 256 个不同的字符。

在世界范围内，陆续出现了一批适用于不同地区的 EASCII 字符集。这些字符集的前 128 个字符统一为 ASCII 码，后 128 个字符定义不同，以适应不同语言的需求。

后来人们发现，EASCII 码仍然无法满足许多语言的字符数量要求。比如汉字有近十万个，光日常使用的就有几千个。中国国家标准总局于 1980 年发布了 GB2312 字符集，其收录了 6763 个汉字，基本满足了汉字的计算机处理需要。

然而，GB2312 无法处理部分罕见字和繁体字。GBK 字符集是在 GB2312 的基础上扩展得到的，它共收录了 21886 个汉字。在 GBK 的编码方案中，ASCII 字符使用一个字节表示，汉字使用两个字节表示。

Unicode 字符集

如果推出一个足够完整的字符集，将世界范围内的所有语言和符号都收录其中，不就可以解决跨语言环境和乱码问题了吗？在这种想法的驱动下，一个大而全的字符集 Unicode 应运而生。

Unicode 的中文名称为“统一码”，理论上能容纳 100 多万个字符。它致力于将全球范围内的字符纳入统一的字符集之中，提供一种通用的字符集来处理和显示各种语言文字，减少因为编码标准不同而产生的乱码问题。

自 1991 年发布以来，Unicode 不断扩充新的语言与字符。截至 2022 年 9 月，Unicode 已经包含 149186 个字符，包括各种语言的字符、符号甚至表情符号等。在庞大的 Unicode 字符集中，常用的字符占用 2 字节，有些生僻的字符占用 3 字节甚至 4 字节。

Unicode 是一种通用字符集，本质上是给每个字符分配一个编号（称为“码点”），但它并没有规定在计算机中如何存储这些字符码点。我们不禁会问：当多种长度的 Unicode 码点同时出现在一个文本中时，系统如何解析字符？例如给定一个长度为 2 字节的编码，系统如何确认它是一个 2 字节的字符还是两个 1 字节的字符？

对于以上问题，一种直接的解决方案是将所有字符存储为等长的编码。如图 3-7 所示，“Hello”中的每个字符占用 1 字节，“算法”中的每个字符占用 2 字节。我们可以通过高位填 0 将“Hello 算法”中的所有字符都编码为 2 字节长度。这样系统就可以每隔 2 字节解析一个字符，恢复这个短语的内容了。

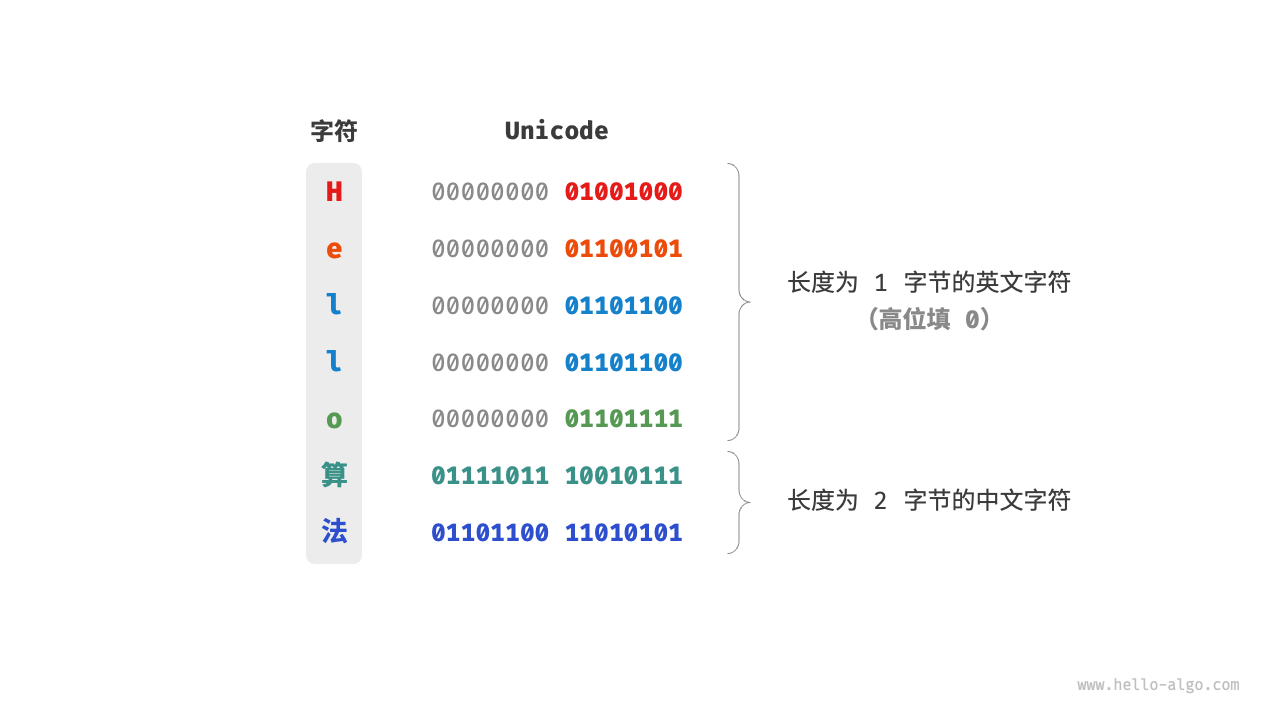
然而 ASCII 码已经向我们证明，编码英文只需 1 字节。若采用上述方案，英文文本占用空间的大小将会是 ASCII 编码下的两倍，非常浪费内存空间。因此，我们需要一种更加高效的 Unicode 编码方法。

UTF-8 编码

目前，UTF-8 已成为国际上使用最广泛的 Unicode 编码方法。它是一种可变长度的编码，使用 1 到 4 字节来表示一个字符，根据字符的复杂性而变。ASCII 字符只需 1 字节，拉丁字母和希腊字母需要 2 字节，常用的中文字符需要 3 字节，其他的一些生僻字符需要 4 字节。

以上讨论的都是字符串在编程语言中的存储方式，这和字符串如何在文件中存储或在网络中传输是不同的问题。在文件存储或网络传输中，我们通常会将字符串编码为 UTF-8 格式，以达到最优的兼容性和空间效率。

# 数据结构 # 算法 # python
Logo
北京朝阳AI社区

更多推荐

构建电商智能营销自动化平台

电商智能营销自动化平台旨在通过人工智能技术提升电商企业的营销效率和转化率。平台架构设计原则核心算法实现细节数据建模方法实际应用案例分析本文重点聚焦于技术实现层面，而非商业策略讨论。首先介绍核心概念和平台架构然后深入算法原理和数学模型接着提供完整的代码实现案例最后讨论实际应用和发展趋势用户画像(User Profile): 通过收集和分析用户行为数据构建的综合性用户特征描述协同过滤(Collabor

avatar 北京朝阳AI社区

【路径规划】基于RRT算法和帕累托最优的多智能体去中心化路径规划附matlab代码

本文针对多智能体协同路径规划的核心痛点，完善并优化了“去中心化架构 + 改进 RRT 搜索 + 帕累托多目标优化”方案，补充了冲突消解细化逻辑、动态协同机制及完整可视化模块。方案无需中心控制器，每个智能体独立决策并通过局部通信避碰，同时平衡 “路径最短、安全距离最大、能耗最低” 三大目标，适用于无人机集群、AGV 车间调度、机器人协同作业等场景，附可直接运行的完整代码与结果分析！

avatar 北京朝阳AI社区

基于超级领航-虚拟领航-跟随三级架构的4艘欠驱动USV围捕控制Matlab仿真，通过人工势场APF实现障碍规避与USV间防碰撞，结合事件触发机制ETM降低通信负担，同时在复合扰动下保持围捕编队，更贴近

本文针对多智能体协同路径规划的核心痛点，完善并优化了“去中心化架构 + 改进 RRT 搜索 + 帕累托多目标优化”方案，补充了冲突消解细化逻辑、动态协同机制及完整可视化模块。方案无需中心控制器，每个智能体独立决策并通过局部通信避碰，同时平衡 “路径最短、安全距离最大、能耗最低” 三大目标，适用于无人机集群、AGV 车间调度、机器人协同作业等场景，附可直接运行的完整代码与结果分析！

avatar 北京朝阳AI社区