LFM信号分析_附MATLAB实现代码

下图给出了矩形窗和加Hamming窗的脉冲压缩结果，Hamming又称改进版的升余弦窗，与矩形窗相比，Hamming窗将PSLR降低至-40.61dB，有效地抑制了副瓣的幅度，其幅度比加Hanning窗时要更低；时即为矩形窗)和Kaiser窗的对比，与矩形窗相比，Kaiser窗将PSLR降低至-20.67dB(近似为幅度的1/10)，ISLR降低至-18.45dB，但分辨率扩展了1.18倍，由于窗

SmallC1oud

6432人浏览 · 2023-11-28 15:12:32

SmallC1oud · 2023-11-28 15:12:32 发布

LFM信号

在时域中，理想线性调频信号持续时间为 $T$ 秒，振幅为一常量，中心频率为 $f_{center}$ ，相位 $θ(t)\theta(t)$ 随时间按一定规律变化。当 $f_{center}$ 为0时，信号的复数形式为

$\left( \frac{t}{T} \right) e^{ j \pi K t^2 }$

其中， $t$ 是时间变量， $K$ 是线性调频率，单位为 $Hz / s$ 。

瞬时频率：

$f = K t$

由于频率的线性调制，相位是时间的二次函数：

$ϕ(t)=πKt2\phi(t) = \pi K t^2$

信号带宽是斜率及其持续时间的乘积：

$\left| K \right| T$

时间带宽积(TBP)是带宽和持续时间的乘积，该参数是无量纲的：

$\left|K\right| T^2$

线性调频信号的频谱，难以直接推导，可利用驻定相位原理得到简单的近似表达式。

驻定相位原理(POSP)：

信号相位包含二次及更高次，在相位驻留点附近是缓变的，而在其他时间点上是捷变的，相位捷变处由于相位周期的正负部分相互抵消，故其对积分的贡献几乎为零，对积分起主要作用的部分集中在相位驻留点附近。

信号带宽为200MHz，脉冲持续时间为 $\mu s$ ，过采样率取 $αos=1.25\alpha_{os}=1.25$ 时的基带LFM信号的时域波形和频谱图如下图所示。

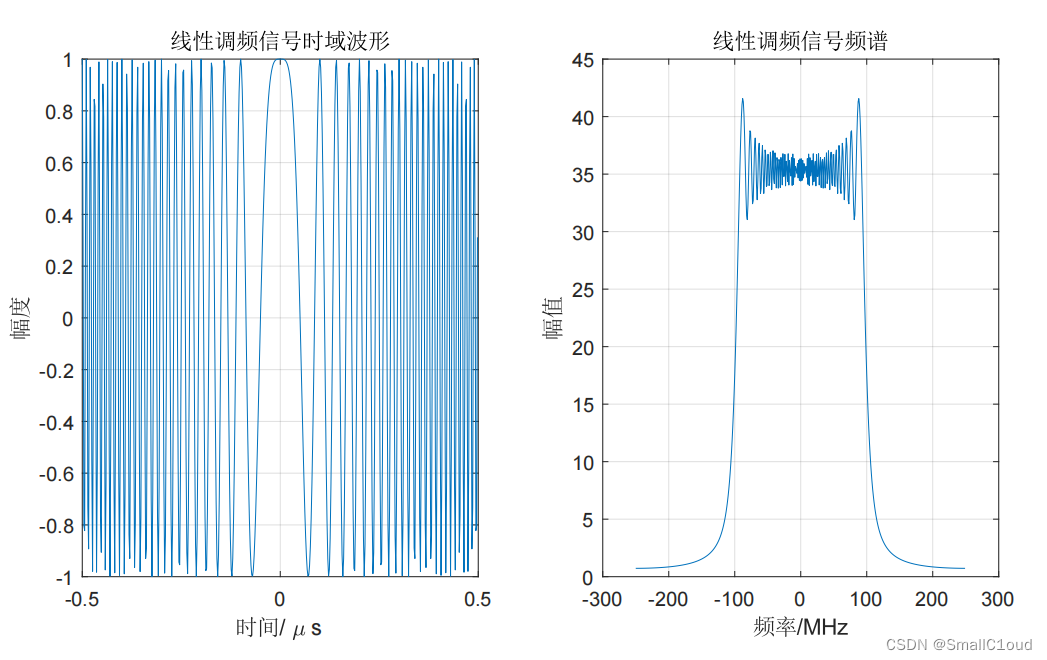
在这里插入图片描述

下图给出了基带LFM信号的瞬时相位和瞬时频率，其相位是二次的，其频率是时间的线性函数，频率斜率是线性调频率，由于和鸟鸣很相似，故线性调频信号常被称为Chirp信号。

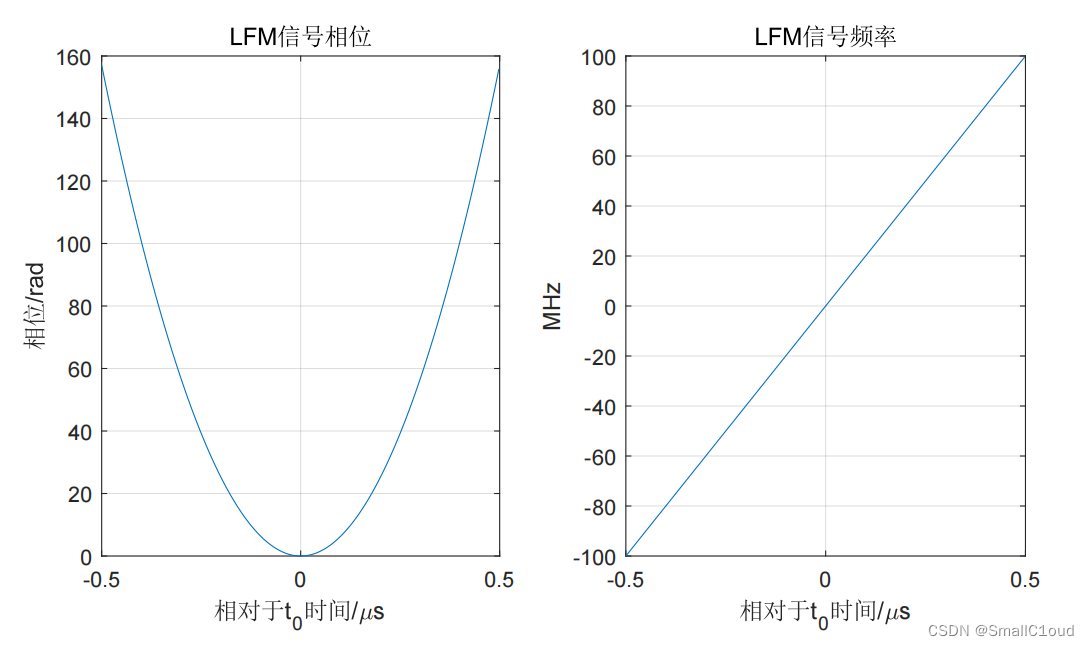
在这里插入图片描述

下图给出了TBP=200时，过采样率 $αos=1.25\alpha_{os}=1.25$ 时通过DFT而不是POSP得到的线性调频脉冲频谱，由于在DFT后进行了 $ff t s hi f t$ (左/右半边互换)操作，故零频位于序列中心。可以看出，频谱的实部和虚部具有和LFM相似的线性调频结构，与LFM信号不同的是频谱存在 $π/4\pi / 4$ 的相位差，且调频率发生了变化；频谱的幅度可以近似为矩形窗函数；频谱的相位与LFM信号的相位基本一致，可近似为一个关于频率的二次函数。

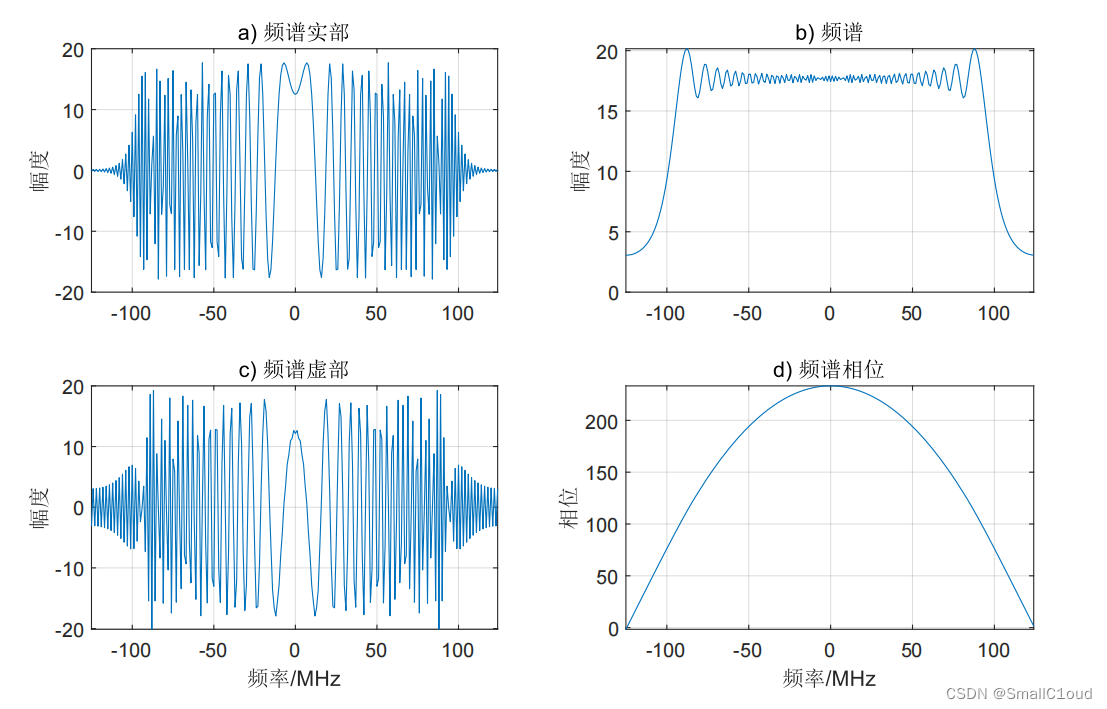
在这里插入图片描述

探究不同过采样率下的DFT结果

基带复线性调频信号的最高频率为带宽的一半，所以最低复采样率 $f_s$ 必须大于带宽。检验采样率充分性的另一种方法就是寻找采样信号频谱中的间隙，如果间隙不存在，则采样率过小；如果间隙高于采样率的20%，采样率就大于最优效率值。

为了衡量能量间隙的相对大小，定义过采样因子为 $αos=fs∣K∣T\alpha_{os} = \frac{f_s}{\left|K\right| T }$

图 \ref{不同过采样率下的信号实部和频谱幅度-在频谱中引起的能量间隙} 给出了不同过采样率下LFM信号补零后的能量间隙。可以看出：随着过采样率以0.2的间隔逐步降低，能量间隙也相应减少，间隙也可以看成是未被利用的频谱空间。 $αos=1.2\alpha_{os}=1.2$ 时，频谱中存在一个很小但很清晰的间隙，说明此时这一过采样值较好地兼顾了效率和精度； $αos=1\alpha_{os}=1$ 时，间隙消失，虽然严格来说此时不会出现混叠，但由于存在标称带宽范围外的频率泄露，仍会发生少量混叠；当 $αos=0.8\alpha_{os}=0.8$ 时，存在严重的混叠，较低和较高部分的频谱交织在一起，无法区分。因此为了保留连续信号的信息， $αos\alpha_{os}$ 必须大于1，通常取在 1.1 ~1.4之间。

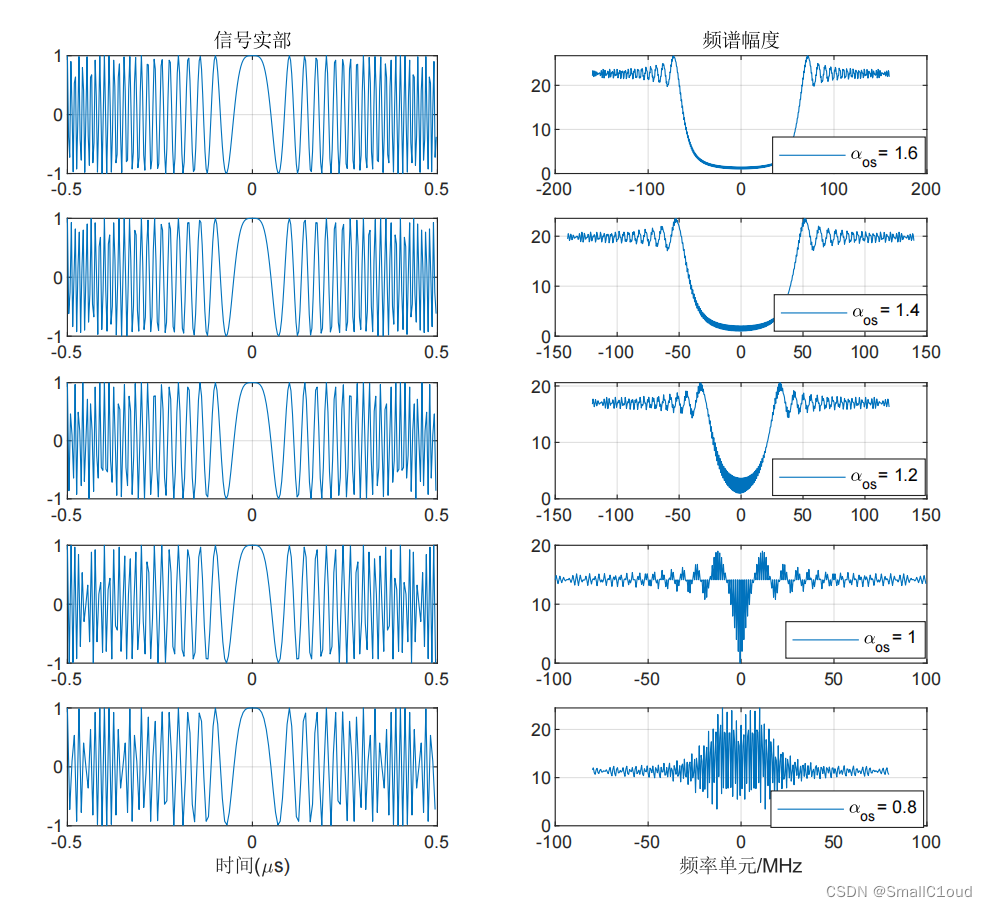
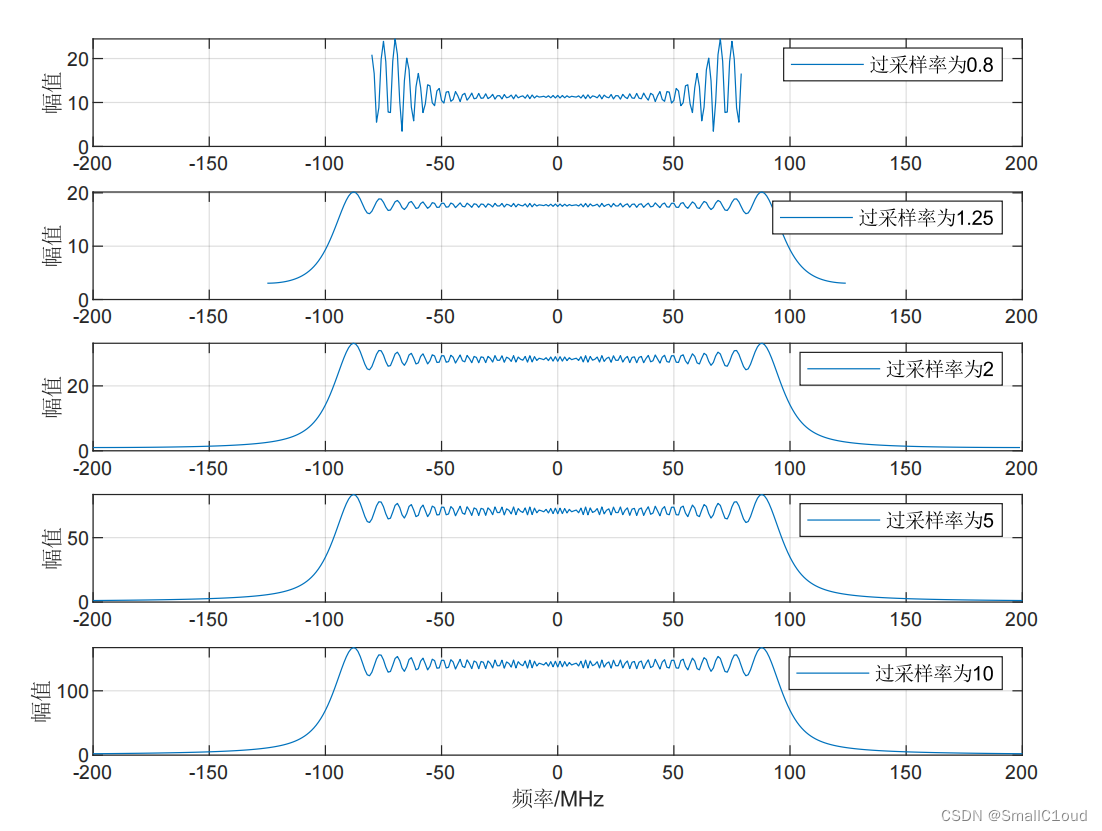
在这里插入图片描述
下图给出了不同过采样率下的信号频谱，当 $αos=0.8\alpha_{os}=0.8$ 时，采样率不足以恢复出原信号，其对应的频谱缺失了一部分；当 $αos>1\alpha_{os}>1$ 时，能较好地恢复原信号，频谱近似于矩形窗。实际中，为了有效利用数据点数，同时保证能正确恢复信号，通常取 $αos≈1.2\alpha_{os} \approx 1.2$ 。

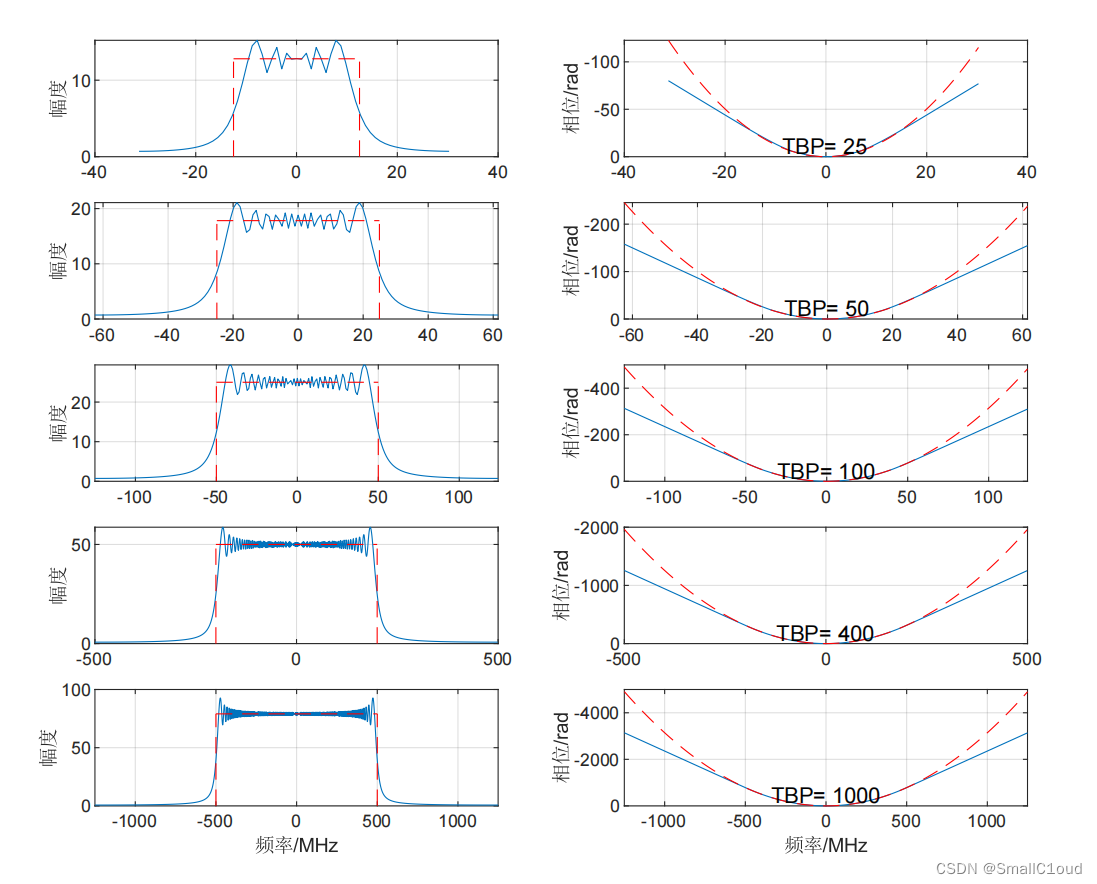
在这里插入图片描述

下图给出了不同TBP时的LFM信号频谱图，由左边一列可以看出，随着TBP的增大，信号频谱幅度越接近矩形窗，当TBP<100时，近似效果较差；TBP>100时，近似效果较好，且随着TBP的增大，频域上的吉布斯效应不会消失。在SAR信号处理中，通常取较大的TBP。

在这里插入图片描述

统计指标

IRW冲激响应宽度，指冲激响应的3dB宽度，其数值等于脉冲分辨率，时间量纲下的3dB分辨率可以表示为
$ρ=0.886∣K∣T≈1∣K∣T\rho = \frac{0.886}{| K | T} \approx \frac{1}{| K | T}$

PSLR最大旁瓣与主瓣峰值的高度比，称为峰值旁瓣比。
$PSLR=10log10(PsidelobePmainlobe)PSLR=10log_{10} \left( \frac{P_{sidelobe}}{P_{mainlobe}} \right)$

ISLR积分旁瓣比，旁瓣能量与主瓣能量的比值(计算中主峰和旁瓣以靠近峰值的两个零点为分界线)
$ISLR=10log10(Ptotal−PmainPmain)ISLR=10log_{10} \left( \frac{P_{total}-P_{main}}{P_{main}} \right)$

基带LFM信号脉冲压缩的实现

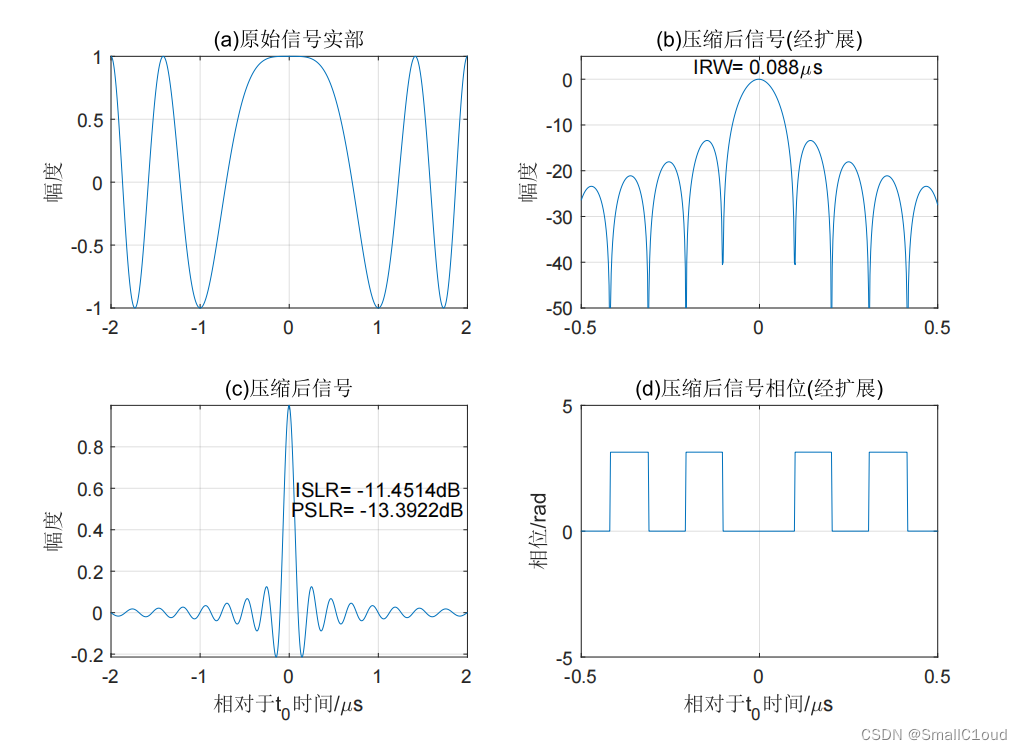
下图给出了基带LFM信号的脉冲压缩示意，信号长 $10μs10\mu s$ ，TBP为100。图\ref{基带LFM信号的脉冲压缩abcd}(a)给出了原始信号实部；由图(b)可以看出，压缩脉冲3dB宽约为 $\mu s$ ，压缩比和TBP近似相等，约为100；图中©给出了经脉冲压缩后的峰值旁瓣比(PSLR)约为-13dB，积分旁瓣比(ISLR)约为-11.5dB；由于不含噪声，故主瓣及偶数旁瓣中的相位为零。

在这里插入图片描述

探究频域加窗的影响

由于线性调频信号存在一一对应的时频关系，所以可以在时域加窗，还可以在时域设计无窗匹配滤波器，直至在频域处理数据时再加窗。

频谱为矩形窗时，对应的时域脉冲的峰值旁瓣比(PSLR)为-13.2 $d B$ ，一般认为这一PSLR过高，因为在图像中会淹没附近的弱目标。实际SAR处理中，通常要求PSLR在-20 $d B$ 以下，ISLR在-17 $d B$ 以下，降低PSLR的一种方法是在频域引入平滑窗，以减少主瓣到旁瓣的能量泄露，从而避免弱目标主瓣被临近强目标的旁瓣淹没。

典型窗包括Taylor窗、Chebyshev窗、Hanning窗、Hamming窗和Kaiser窗。本节主要仿真分析了Hanning窗、Hamming窗和Kaiser窗对脉冲压缩的影响。

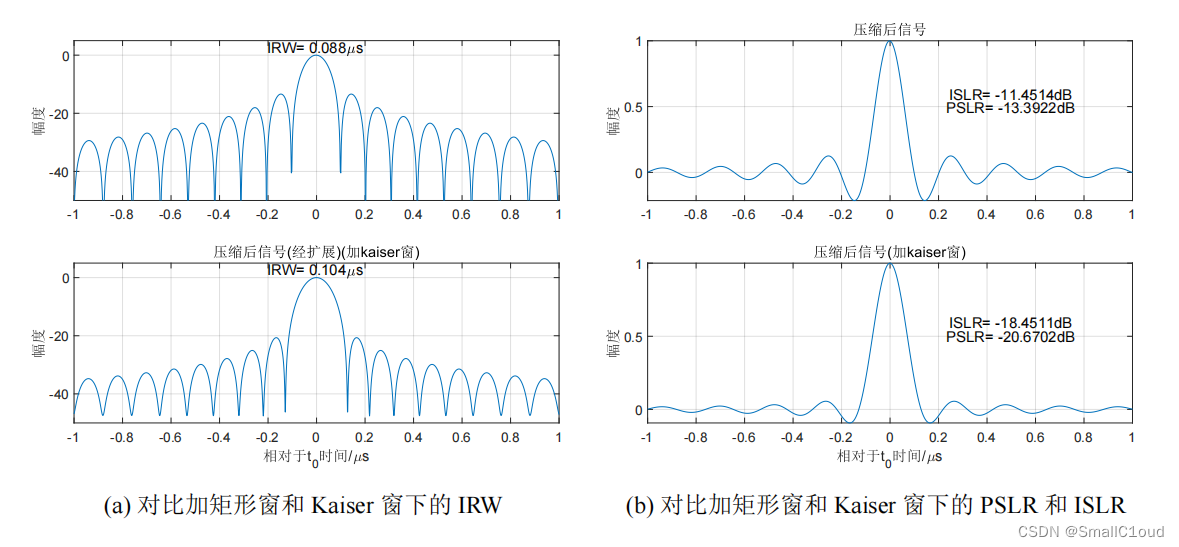
Kaiser窗是一种似长球波函数，其能在一定的ISLR下，近乎最优地使脉冲压缩的主瓣能量达到最大；Kaiser有一个可调节参数 $β\beta$ ,可以在不同应用中兼顾分辨率和旁瓣。下图给出了在 $β=2.5\beta = 2.5$ 时加矩形窗(Kaiser窗的 $β=0\beta = 0$ 时即为矩形窗)和Kaiser窗的对比，与矩形窗相比，Kaiser窗将PSLR降低至-20.67dB(近似为幅度的1/10)，ISLR降低至-18.45dB，但分辨率扩展了1.18倍，由于窗的展宽效应可以抵消式\ref{脉冲分辨率}中的0.886，故其可忽略不计。.

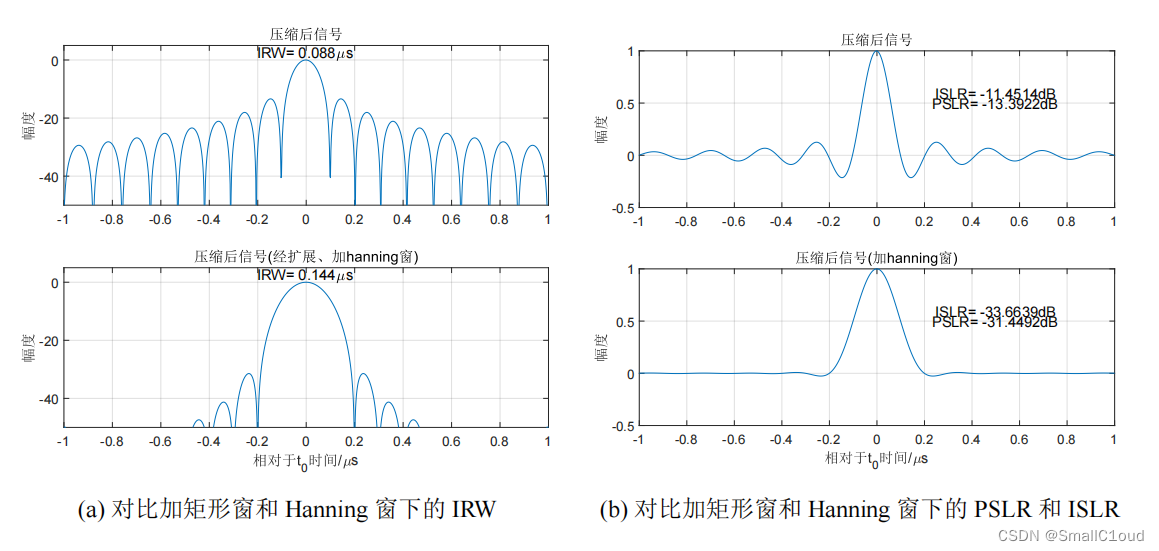
在这里插入图片描述
下图给出了矩形窗和加Hanning窗的脉冲压缩结果，与矩形窗相比，Hanning窗将PSLR降低至-31.45dB，有效地抑制了副瓣的幅度，有利于提高信号的动态范围；ISLR降低至-33.66dB，使得能量集中在主瓣当中；分辨率扩展了1.64倍，一定程度上降低了分辨能力。总的来说，使用Hanning窗进行频域加窗处理可以改善脉冲压缩的副瓣抑制效果，但会导致脉冲宽度的增加(即分辨率降低)。

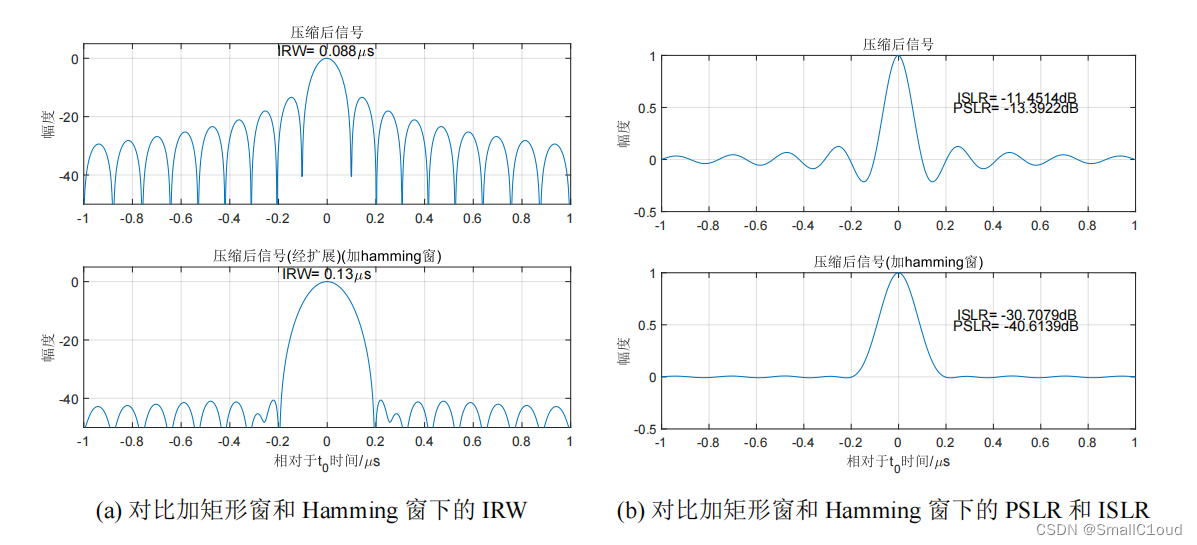
在这里插入图片描述

下图给出了矩形窗和加Hamming窗的脉冲压缩结果，Hamming又称改进版的升余弦窗，与矩形窗相比，Hamming窗将PSLR降低至-40.61dB，有效地抑制了副瓣的幅度，其幅度比加Hanning窗时要更低；ISLR降低至-30.71dB，使得能量集中在主瓣当中；分辨率扩展了1.48倍，一定程度上降低了分辨能力。总的来说，使用Hamming窗进行频域加窗处理可以改善脉冲压缩的副瓣抑制效果，但会导致脉冲宽度的增加(即分辨率降低)。

在这里插入图片描述

小结：窗是一个对信号频谱进行加权的实函数。权值在信号中心频谱处最大，向频谱两边逐渐衰落，窗能够平滑频谱，即弱化频谱边缘处的不连续性，从而降低时域脉冲的主瓣能量泄露，但要以损失分辨率为代价，故须折中考虑。

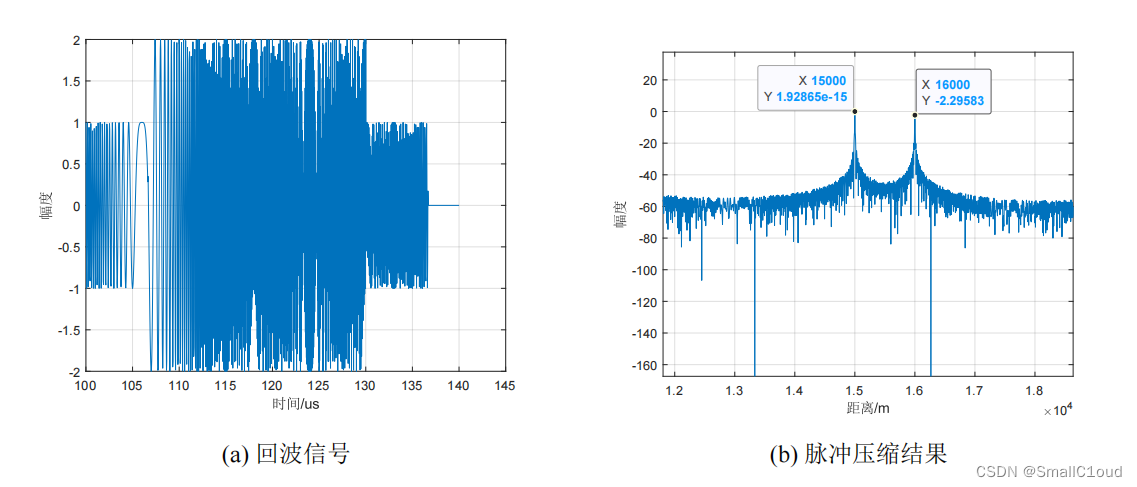
回波信号的脉冲压缩

在这里插入图片描述

% 1.LFM信号分析
% （1）仿真LFM信号；
% （2）观察不同过采样率下的DFT结果；
% （3）观察不同TBP的LFM信号的频谱。
clc;clear;close all
%% （1）仿真LFM信号   仅供参考！！！
%% 参数设置
B = 2e8;            % 200MHz
T = 1e-6;           % 脉冲持续时间
K = B/T;            % 调频斜率    B=K*T
alpha_os = 1.25;     % 过采样率   alpha_os=fs/(K*T)
fs = alpha_os*B;    % 采样率
N = round( T / (1/fs) );% 采样点数
dt = T/N;               % 采样时间间隔
df = fs/N;              % 采样频率间隔
t = -T/2:dt:T/2-dt;     % 时间变量
freq = -fs/2:df:fs/2-df;% 频率变量
A_lfm = 1;              % 设置信号幅度
f_lfm = 0;              % 设置信号载频频率
y_lfm = A_lfm*exp(1j*(2*pi*f_lfm*t+pi*K*t.^2)); % 信号表达式
f = K*t;                   % 瞬时频率
phi = pi*K*t.^2;           % 瞬时相位

%% 绘制时域图
figure
subplot(121),plot(1e6*t,real(y_lfm));    % 绘制时域图
grid on;
xlabel('时间/ \mu s');           
ylabel('幅度');        
title( '线性调频信号时域波形');              
%% 绘制频谱图
Sf = fftshift(fft(fftshift(y_lfm)));  
subplot(122),plot(freq/1e6,abs(Sf) );    % 绘制频谱图
grid on;
xlabel('频率/MHz');          
ylabel('幅值');          
title('线性调频信号频谱');   

%% 绘制瞬时相位、瞬时频率图像
figure
subplot(121)
plot(t*1e+6,phi);grid on;
title('LFM信号相位');
xlabel('相对于t_0时间/\mus');
ylabel('相位/rad')
subplot(122)
plot(t*1e+6,f*1e-6);grid on;
title('LFM信号频率');
xlabel('相对于t_0时间/\mus');
ylabel('MHz');

%% 
TBP = 200;
T = 1e-6;        % 脉冲持续时间
B = TBP/T;
K = B/T;         % 调频斜率
alpha_os = 1.25; % 过采样率
fs = alpha_os*B; % 采样率
N = round( T / (1/fs) );        % 采样点数
dt = T/N;               % 采样时间间隔
df = fs/N;              % 采样频率间隔
t = -T/2:dt:T/2-dt;     % 时间变量
% t = 0:dt:T-dt;
freq = -fs/2:df:fs/2-df;% 频率变量
A_lfm = 1;   % 设置信号幅度
f_lfm = 0;   % 设置信号载频频率
y_lfm = A_lfm*exp(1j*(2*pi*f_lfm*t+pi*K*t.^2)); % 信号表达式
Sf = fftshift(fft(fftshift(y_lfm)));    % Chirp信号频谱表达式
figure
subplot(221),plot(freq*1e-6,real(Sf)),grid on
% axis([-40 40 -20 20])
title('a) 频谱实部'),ylabel('幅度')
subplot(222),plot(freq*1e-6,abs(Sf)),grid on
% axis([-20 20 0 40])
title('b) 频谱'),ylabel('幅度')
subplot(223),plot(freq*1e-6,imag(Sf)),grid on
% axis([-40 40 -20 20])
title('c) 频谱虚部'),xlabel('频率/MHz'),ylabel('幅度')
subplot(224),plot(freq*1e-6,unwrap(angle(Sf))),grid on
%axis([-50 50,0 900])
title('d) 频谱相位'),xlabel('频率/MHz'),ylabel('相位')
% title('线性调频信号的复频谱')

%% ======================================================================== %%
%% （2）观察不同过采样率下的DFT结果    仅供参考！！！
alpha_0 = [0.8 1 1.2 1.4];% 过采样率
figure
for i = 1:length(alpha_0)
    TBP = 200;
    T = 1e-6; % 脉冲持续时间
    B = TBP/T;
    K = B/T;  % 调频斜率
    fs = alpha_0(i)*B; % 采样率
    N = round( T / (1/fs) );        % 采样点数
    dt = T/N;              % 采样时间间隔
    df = fs/N;              % 采样频率间隔
    t = -T/2:dt:T/2-dt;    % 时间变量
    freq = -fs/2:df:fs/2-df; % 频率变量
    A_lfm = 1;     % 设置信号幅度
    f_lfm = 0;   % 设置信号载频频率
    y_lfm = A_lfm*exp(1j*(2*pi*f_lfm*t+pi*K*t.^2)); % 信号表达式
    Sf = fftshift(fft(fftshift(y_lfm)));    % Chirp信号频谱表达式
    %% 绘制频谱图
    subplot(length(alpha_0),1,i);
    plot(freq/1e6,abs(Sf) );grid on;
    axis([-200 200 0 inf]);
    if i==length(alpha_0)
        xlabel('频率/MHz');          
    end
    ylabel('幅值');          
    % title(['过采样率为',num2str(alpha_0(i))]); 
    % text(0,alpha_0(i),['过采样率为',num2str(alpha_0(i))],'HorizontalAlignment','center')
    legend(['过采样率为',num2str(alpha_0(i))])
end

% 参数设置
TBP = 200;             % 时间带宽积
T = 1e-6;             % 脉冲持续时间
alpha_0 = [1.6 1.4 1.2 1.0 0.8];             % 过采样率
figure; % title('过采样率\alpha_{os}在频谱中引起的能量间隙');
for i=1:length(alpha_0)
    % 参数计算
    B = TBP/T;             % 信号带宽
    K = B/T;               % 线性调频频率
    F = alpha_0(i)*B;     % 采样频率
    N = 2*ceil(F*T/2);     % 采样点数
    dt = T/N;              % 采样时间间隔
    df = F/N;              % 采样频率间隔
    % 变量设置
    t = -T/2:dt:T/2-dt;    % 时间变量
    f = -F/2:df:F/2-df;    % 频率变量
    f_zero = -F/2:F/(2*N):F/2-F/(2*N);    % 补零后的频率变零
    % 信号表达
    st = exp(1j*pi*K*t.^2);               % Chirp信号复数表达式
    Sf1 = fft(fftshift(st));              % Chirp信号频谱表达式
    st_zero = [st,zeros(1,N)];            % Chirp信号补零表达式
    Sf2 = fft(fftshift(st_zero));         % Chirp信号补零后的频谱表达式
    % 绘图
    subplot(length(alpha_0),2,2*i-1),plot(t*1e+6,real(st)),grid on
    if(i==1)
        title('信号实部')
    end
    if(i==length(alpha_0))
        xlabel('时间(\mus)')
    end
    subplot(length(alpha_0),2,2*i),plot(f_zero*1e-6,abs(Sf2)),grid on
    if(i==1)
        title('频谱幅度')
    end
    if(i==length(alpha_0))
        xlabel('频率单元/MHz')
    end
    % text(2.7,18,['\alpha_{os}= ',num2str(alpha_0(i))],'HorizontalAlignment','center')
    legend(['\alpha_{os}= ',num2str(alpha_0(i))])
end
%% ======================================================================== %%
%% （3）观察不同TBP的LFM信号的频谱   仅供参考！！！
TBP = [25,50,100,400,1000]; % 时间带宽积
figure
for i = 1:length(TBP)
    T = 1e-6;                  % 脉冲持续时间
    B = TBP(i)/T;
    K = B/T;  % 调频斜率
    alpha_os = 2.5;% 过采样率
    fs = alpha_os*B; % 采样率
    N = round( T / (1/fs) );        % 采样点数
    t = linspace( -T/2 , T/2 , N);  % 
    y_lfm = A_lfm*exp(1j*(2*pi*f_lfm*t+pi*K*t.^2)); % 信号表达式

    %% 绘制频谱图
    freq = linspace(-fs/2,fs/2,N);  % 频域采样选取采样点，在-fs/2与fs/2间生成N个点
    Sf = fftshift( fft(y_lfm) );    
    subplot(length(TBP),1,i);
    plot(freq/1e6,abs(Sf) ),grid on;
    % axis([-200 200 0 1800]);
    if i==length(TBP)
        xlabel('频率/MHz');           
    end
    ylabel('幅度');  
    % title(['TBP为',num2str(TBP(i))]);
    legend(['TBP为',num2str(TBP(i))]);
end

TBP = [25,50,100,400,1000]; % 时间带宽积
figure
for i = 1:length(TBP)
    % 参数设置
    T = 1e-6;              % 脉冲持续时间
    B = TBP(i)/T;          % 信号带宽
    K = B/T;               % 线性调频频率
    alpha_os = 2.5;        % 过采样率
    F = alpha_os*B;        % 采样频率
    N = 2*ceil(F*T/2);     % 采样点数
    dt = T/N;              % 采样时间间隔
    df = F/N;              % 采样频率间隔
    % 变量设置
    t = -T/2:dt:T/2-dt;    % 时间变量
    freq = -F/2:df:F/2-df; % 频率变量
    % 信号表达
    y_lfm = A_lfm*exp(1j*(2*pi*f_lfm*t+pi*K*t.^2)); % 信号表达式
    Sf = fftshift(fft(fftshift(y_lfm)));     % Chirp信号频谱表达式
    %% 绘图
    % 频谱幅度
    subplot(5,2,2*i-1)
    plot(freq*1e-6,abs(Sf)),grid on
    if(i==5)
        xlabel('频率/MHz')
    end
    ylabel('幅度')
    line([-B*1e-6/2,-B*1e-6/2],[0,sqrt(1/K)*1e+6*N],'color','r','linestyle','--')
    line([ B*1e-6/2, B*1e-6/2],[0,sqrt(1/K)*1e+6*N],'color','r','linestyle','--')
    line([-B*1e-6/2, B*1e-6/2],[sqrt(1/K)*1e+6*N,sqrt(1/K)*1e+6*N],'color','r','linestyle','--')
    % 频谱相位
    subplot(5,2,2*i)
    plot(freq*1e-6,unwrap(angle(Sf))-max(unwrap(angle(Sf)))),hold on,grid on
    plot(freq*1e-6,(-pi*freq.^2/K)-max(-pi*freq.^2/K),'r--');
    set(gca,'YDir','reverse')    % 设置坐标轴翻转
    if(i==5)
        xlabel('频率/MHz')
    end
    ylabel('相位/rad')
    text(0,-TBP(i)/2,['TBP= ',num2str(TBP(i))],'HorizontalAlignment','center')
end

% 2.针对"基带LFM信号"实现脉冲压缩仿真
% （1）实现无误差的脉冲压缩，计算指标（IRW、PSLR、ISLR）
% （2）观察频域加窗的影响，计算指标（IRW、PSLR、ISLR）
clc;clear;close all
%% （1）针对"基带LFM信号",实现无误差的脉冲压缩，计算指标（IRW、PSLR、ISLR）   仅供参考！！！
% 参数设置
TBP = [10 100];            % 时间带宽积
figure
for i=1:length(TBP)
    T = 10e-6;             % 脉冲持续时间
    % 参数计算
    B = TBP(i)/T;          % 信号带宽
    K = B/T;               % 线性调频频率
    alpha_os = 50;         % 过采样率，使用较高的过采样率是为了提高采样频率
    F = alpha_os*B;        % 采样频率
    N = 2*ceil(F*T/2);     % 采样点数
    dt = T/N;              % 采样时间间隔
    df = F/N;              % 采样频率间隔
    % 变量设置
    t = -T/2:dt:T/2-dt;    % 时间变量
    freq = -F/2:df:F/2-df;    % 频率变量
    t_out = linspace(2*t(1),2*t(end),2*length(t)-1);    % 循环卷积后的信号长度    
    % 信号表达
    st = exp(1j*pi*K*t.^2);               % Chirp信号复数表达式
    ht = conj(fliplr(st));                % 时域匹配滤波器
    sout = conv(st,ht);                   % 匹配滤波器输出
    sout = sout/max(sout);                % 归一化
    % 绘图
    subplot(1,length(TBP),i)
    plot(t_out*1e+6,real(sout)),grid on
    title(['TBP为',num2str(TBP(i))])
    axis([-4 4,-inf inf])
    xlabel('时间/\mus'),ylabel('幅度')
    % line([-1,1],[ 0,  0],'Color','k')
    % line([ 0,0],[-0.4,1.2],'Color','k')
    % line([-1,-0.05],[0.707,0.707],'Color','k','LineStyle','--')
    % line([ 0.05, 1],[0.707,0.707],'Color','k','LineStyle','--')
    % arrow([-0.3,0.707],[-0.05,0.707]);
    % arrow([ 0.3,0.707],[ 0.05,0.707]);
    % suptitle('匹配滤波器输出的3dB分辨率的测量')
end


t_out = linspace(2*t(1),2*t(end),2*length(t)-1);    % 循环卷积后的信号长度    
% 信号表达
st = exp(1j*pi*K*t.^2);               % Chirp信号复数表达式
ht = conj(fliplr(st));                % 时域匹配滤波器
sout = conv(st,ht);                   % 匹配滤波器输出
% 信号变换
sout_nor = sout/max(sout);                          % 单位化
sout_log = 20*log10(abs(sout)./max(abs(sout))+eps); % 归一化
% 绘图
figure
subplot(221),plot(t*1e+6,real(st)),grid on
axis([-2 2,-inf inf])
title('(a)原始信号实部'),ylabel('幅度')

subplot(222),plot(t_out*1e+6,sout_log),grid on
axis([-0.5 0.5,-50 5])
title('(b)压缩后信号(经扩展)'),ylabel('幅度')
pslr = get_pslr(sout_log);
islr=get_islr(sout_nor);
hw = get_hw(sout_log);
hw = hw*dt;
% 压缩脉冲3dB宽度
% text(0,3,['PSLR= ',num2str(pslr),'dB'],'HorizontalAlignment','center')
text(0,3,['IRW= ',num2str(hw*1e+6),'\mus'],'HorizontalAlignment','center')

subplot(223),plot(t_out*1e+6,real(sout_nor)),grid on
axis([-2 2,-inf inf])
title('(c)压缩后信号')
xlabel('相对于t_0时间/\mus'),ylabel('幅度')
text(1,0.5,['PSLR= ',num2str(pslr),'dB'],'HorizontalAlignment','center')
text(1,0.6,['ISLR= ',num2str(real(islr)),'dB'],'HorizontalAlignment','center')

subplot(224),plot(t_out*1e+6,abs(angle(sout_nor))),grid on
axis([-0.5 0.5,-5 5])
title('(d)压缩后信号相位(经扩展)'),xlabel('相对于t_0时间/\mus'),ylabel('相位/rad')
% suptitle('基带线性调频信号的匹配滤波')

%% （2）观察频域加窗的影响，计算指标（IRW、PSLR、ISLR）     仅供参考！！！
% 参数设置
TBP = 100;             % 时间带宽积
T = 10e-6;             % 脉冲持续时间
B = TBP/T;             % 信号带宽
K = B/T;               % 线性调频频率
alpha_os = 1.25;       % 过采样率
F = alpha_os*B;        % 采样频率
N = 2*ceil(F*T/2);     % 采样点数
dt = T/N;              % 采样时间间隔
df = F/N;              % 采样频率间隔
% 变量设置
t = -T/2:dt:T/2-dt;    % 时间变量
freq = -F/2:df:F/2-df; % 频率变量
% 信号表达
st = exp(1j*pi*K*t.^2);           % Chirp信号复数表达式
Sf = fft((st));                   % Chirp信号频谱表达式
Hf = exp(1j*pi*freq.^2/K);        % 频域匹配滤波器
% 窗函数
window = kaiser(N,2.5)';          % 时域窗  \beta 的一个典型值为2.5
Window = fftshift(window);        % 频域窗
% 信号变换
st_window = window.*exp(1j*pi*K*t.^2);          % 加窗后的Chirp信号
Hf_Window = Window.*Hf;                         % 加窗后的频域频谱滤波器
Soutf_Window = Hf_Window.*Sf;                   % 加窗后的匹配滤波器输出
% 绘图
figure
subplot(211),plot(freq*1e-6,Window)
axis([-5 5,0 1.2])
title('频域窗函数')
subplot(212),plot(freq*1e-6,real(Soutf_Window))
axis([-5 5,-15 15])
title('加窗后的频谱实部'),xlabel('频率/MHz')


% 参数设置		仅供参考！！！
TBP = 100;             % 时间带宽积
T = 10e-6;             % 脉冲持续时间
B = TBP/T;             % 信号带宽
K = B/T;               % 线性调频频率
alpha_os = 100;        % 过采样率
F = alpha_os*B;        % 采样频率
N = 2*ceil(F*T/2);     % 采样点数
dt = T/N;              % 采样时间间隔
df = F/N;              % 采样频率间隔
% N_fft = 1024;
% 变量设置
t = -T/2:dt:T/2-dt;    % 时间变量
freq = -F/2:df:F/2-df; % 频率变量
% 信号表达
st = exp(1j*pi*K*t.^2);           % Chirp信号复数表达式
Sf = fft(st);                     % Chirp信号频谱表达式
h = zeros(1,N);
for i=1:N
    h(i)=conj(st(N-i+1));
end
Hf = fft(h);        % 频域匹配滤波器
S_out = abs(ifft(Sf.*Hf));
S_out_nor = S_out/max(S_out);
S_out_log = 20*log10(abs(S_out)./max(abs(S_out))+eps);

% 窗函数
window = kaiser(N,2.5)';          % 时域窗  \beta 的一个典型值为2.5
% window = hamming(N)';
h_window = conj(fliplr(st.*window));
L = 2*N-1;
Hf_Window = fft(h_window,L);
% s_W_out = abs(ifft(Sf.*Hf_Window));
s_W_out = ifft(fft(st,L).*Hf_Window);
sout_nor_W = s_W_out/max(s_W_out);                          % 单位化
sout_log_W = 20*log10(abs(s_W_out)./max(abs(s_W_out))+eps); % 归一化
% 绘图
% figure
% plot(Hf_Window);
% figure
% plot(abs(fftshift(Soutf_Window.*window)));%axis([-8 8 -inf inf])
% plot(freq/1e+6,fftshift(Hf_Window));%axis([-6 6 -inf inf])

pslr_W = get_pslr(sout_log_W);
islr_W = get_islr(sout_nor_W);
hw_W = get_hw(sout_log_W);
hw_W = hw_W*dt;

dtt = 2*T/L;
tt = -T:dtt:T-dtt;    % 时间变量
%% 绘图
figure
subplot(211),plot(t_out*1e+6,sout_log),grid on
axis([-1 1,-50 5])
ylabel('幅度')
% 压缩脉冲3dB宽度
text(0,3,['IRW= ',num2str(hw*1e+6),'\mus'],'HorizontalAlignment','center')
subplot(212),plot(tt*1e+6,sout_log_W),grid on
axis([-1 1,-50 5])
title('压缩后信号(经扩展)(加kaiser窗)')
xlabel('相对于t_0时间/\mus'),ylabel('幅度')
% 压缩脉冲3dB宽度
text(0,3,['IRW= ',num2str(hw_W*1e+6),'\mus'],'HorizontalAlignment','center')

figure
subplot(211),plot(t_out*1e+6,real(sout_nor)),grid on
axis([-1 1,-inf inf])
title('压缩后信号')
ylabel('幅度')
text(0.5,0.5,['PSLR= ',num2str(pslr),'dB'],'HorizontalAlignment','center')
text(0.5,0.6,['ISLR= ',num2str(real(islr)),'dB'],'HorizontalAlignment','center')
subplot(212),plot(tt*1e+6,real(sout_nor_W)),grid on
axis([-1 1,-inf inf])
title('压缩后信号(加kaiser窗)')
xlabel('相对于t_0时间/\mus'),ylabel('幅度')
text(0.5,0.5,['PSLR= ',num2str(pslr_W),'dB'],'HorizontalAlignment','center')
text(0.5,0.6,['ISLR= ',num2str(real(islr_W)),'dB'],'HorizontalAlignment','center')


% figure
% subplot(221),plot(t*1e+6,real(st)),grid on
% axis([-2 2,-inf inf])
% title('(a)原始信号实部'),ylabel('幅度')
% 
% subplot(222),plot(tt*1e+6,sout_log_W),grid on
% axis([-1 1,-50 5])
% title('(b)压缩后信号(经扩展)'),ylabel('幅度')
% % 压缩脉冲3dB宽度
% text(0,3,['IRW= ',num2str(hw_W*1e+6),'\mus'],'HorizontalAlignment','center')
% 
% subplot(223),plot(tt*1e+6,real(sout_nor_W)),grid on
% axis([-2 2,-inf inf])
% title('(c)压缩后信号')
% xlabel('相对于t_0时间/\mus'),ylabel('幅度')
% text(1,0.5,['PSLR= ',num2str(pslr_W),'dB'],'HorizontalAlignment','center')
% text(1,0.6,['ISLR= ',num2str(real(islr_W)),'dB'],'HorizontalAlignment','center')
% 
% subplot(224),plot(tt*1e+6,abs(angle(sout_nor_W))),grid on
% axis([-1 1,-5 5])
% title('(d)压缩后信号相位(经扩展)'),xlabel('相对于t_0时间/\mus'),ylabel('相位/rad')

%% 加Hamming窗
window_ham = hamming(N)';
h_window_ham = conj(fliplr(st.*window_ham));
L = 2*N-1;
Hf_Window_ham = fft(h_window_ham,L);
% s_W_out = abs(ifft(Sf.*Hf_Window));
s_W_out_ham = ifft(fft(st,L).*Hf_Window_ham);
sout_nor_W_ham = s_W_out_ham/max(s_W_out_ham);                          % 单位化
sout_log_W_ham = 20*log10(abs(s_W_out_ham)./max(abs(s_W_out_ham))+eps); % 归一化

%% 计算指标
pslr_W_ham = get_pslr(sout_log_W_ham);
islr_W_ham = get_islr(sout_nor_W_ham);
hw_W_ham = get_hw(sout_log_W_ham);
hw_W_ham = hw_W_ham*dt;

dtt = 2*T/L;
tt = -T:dtt:T-dtt;    % 时间变量
%% 绘图
figure
subplot(211),plot(t_out*1e+6,sout_log),grid on
title('压缩后信号'),axis([-1 1,-50 5])
ylabel('幅度')
% 压缩脉冲3dB宽度
text(0,3,['IRW= ',num2str(hw*1e+6),'\mus'],'HorizontalAlignment','center')
subplot(212),plot(tt*1e+6,sout_log_W_ham),grid on
axis([-1 1,-50 5])
title('压缩后信号(经扩展)(加hamming窗)')
xlabel('相对于t_0时间/\mus'),ylabel('幅度')
% 压缩脉冲3dB宽度
text(0,3,['IRW= ',num2str(hw_W_ham*1e+6),'\mus'],'HorizontalAlignment','center')

figure
subplot(211),plot(t_out*1e+6,real(sout_nor)),grid on
axis([-1 1,-0.5 1])
title('压缩后信号')
ylabel('幅度')
text(0.5,0.5,['PSLR= ',num2str(pslr),'dB'],'HorizontalAlignment','center')
text(0.5,0.6,['ISLR= ',num2str(real(islr)),'dB'],'HorizontalAlignment','center')
subplot(212),plot(tt*1e+6,real(sout_nor_W_ham)),grid on
axis([-1 1,-0.5 1])
title('压缩后信号(加hamming窗)')
xlabel('相对于t_0时间/\mus'),ylabel('幅度')
text(0.5,0.5,['PSLR= ',num2str(pslr_W_ham),'dB'],'HorizontalAlignment','center')
text(0.5,0.6,['ISLR= ',num2str(real(islr_W_ham)),'dB'],'HorizontalAlignment','center')

%% 加Hanning窗
window_han = hanning(N)';
h_window_han = conj(fliplr(st.*window_han));
L = 2*N-1;
Hf_Window_han = fft(h_window_han,L);
% s_W_out = abs(ifft(Sf.*Hf_Window));
s_W_out_han = ifft(fft(st,L).*Hf_Window_han);
sout_nor_W_han = s_W_out_han/max(s_W_out_han);                          % 单位化
sout_log_W_han = 20*log10(abs(s_W_out_han)./max(abs(s_W_out_han))+eps); % 归一化

%% 计算指标
pslr_W_han = get_pslr(sout_log_W_han);
islr_W_han = get_islr(sout_nor_W_han);
hw_W_han = get_hw(sout_log_W_han);
hw_W_han = hw_W_han*dt;

dtt = 2*T/L;
tt = -T:dtt:T-dtt;    % 时间变量
%% 绘图
figure
subplot(211),plot(t_out*1e+6,sout_log),grid on
title('压缩后信号'),axis([-1 1,-50 5])
ylabel('幅度')
% 压缩脉冲3dB宽度
text(0,3,['IRW= ',num2str(hw*1e+6),'\mus'],'HorizontalAlignment','center')
subplot(212),plot(tt*1e+6,sout_log_W_han),grid on
axis([-1 1,-50 5])
title('压缩后信号(经扩展、加hanning窗)')
xlabel('相对于t_0时间/\mus'),ylabel('幅度')
% 压缩脉冲3dB宽度
text(0,3,['IRW= ',num2str(hw_W_han*1e+6),'\mus'],'HorizontalAlignment','center')

figure
subplot(211),plot(t_out*1e+6,real(sout_nor)),grid on
axis([-1 1,-0.5 1])
title('压缩后信号'),ylabel('幅度')
text(0.5,0.5,['PSLR= ',num2str(pslr),'dB'],'HorizontalAlignment','center')
text(0.5,0.6,['ISLR= ',num2str(real(islr)),'dB'],'HorizontalAlignment','center')
subplot(212),plot(tt*1e+6,real(sout_nor_W_han)),grid on
axis([-1 1,-0.5 1])
title('压缩后信号(加hanning窗)')
xlabel('相对于t_0时间/\mus'),ylabel('幅度')
text(0.5,0.5,['PSLR= ',num2str(pslr_W_han),'dB'],'HorizontalAlignment','center')
text(0.5,0.6,['ISLR= ',num2str(real(islr_W_han)),'dB'],'HorizontalAlignment','center')
%% 函数实现代码
%% HW函数 IRW 冲激响应的3dB主瓣宽度
function [hw] = get_hw(Af)
    % 找到Af的最大位置
    [~,locmax] = max(Af);
    % 找到locmax左边最接近-3dB的位置
    [~,locleft] = min(abs(Af(1:locmax)+3));
    % 找到locmax右边最接近-3dB的位置
    [~,locright] = min(abs(Af(locmax:end)+3));
    locright = locright + locmax - 1;
    % 得到3dB波束宽度
    hw = locright-locleft;
end
%% PSLR函数 峰值旁瓣比，最大旁瓣与峰值的高度比
function [PSLR] = get_pslr(Af)
    % 找到所有的pesks
    peaks = findpeaks(Af);
    % 对peaks进行降序排列
    peaks = sort(peaks,'descend');
    % 得到第一旁瓣
    PSLR = peaks(2);
end
%
function islr=get_islr(x)

l=length(x);
a=find(x==max(x));
i=1;
for k=a-1:-1:2
    if(x(k)-x(k-1)<0&&x(k)-x(k+1)<0)
        lindian(i)=k;
        i=i+1;
    end
end
lindian1=max(lindian);

lindian=0;
i=1;
for k=a+1:l-1
    if(x(k)-x(k-1)<0&&x(k)-x(k+1)<0)
        lindian(i)=k;
        i=i+1;
    end
end
lindian2=min(lindian);

pmain=0;
for k=lindian1:lindian2
    pmain=pmain+x(k)^2;
end
x=x.^2;
ptotal=sum(x);
islr=10*log10((ptotal-pmain)/ptotal);
end