一.反三角函数

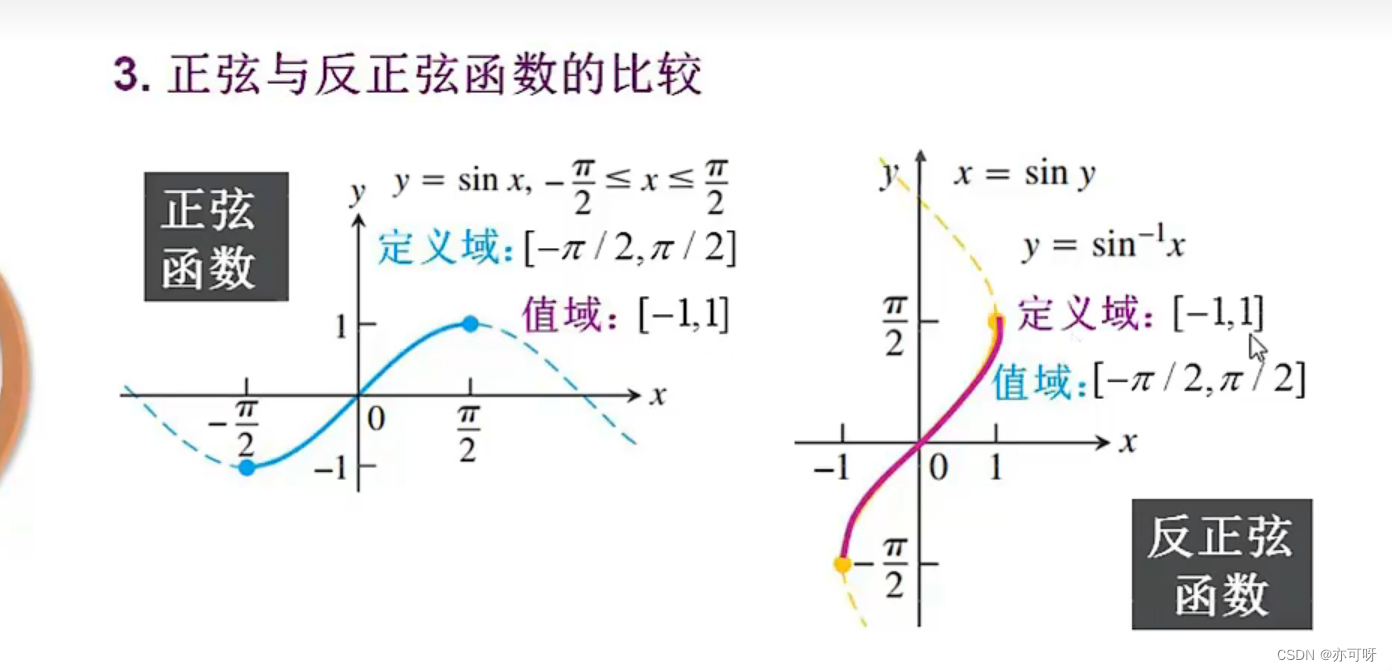
1.1反正弦函数

正弦函数 $y=\sin x$ \quad ($x\in [-\frac{\pi }{2},\frac{\pi }{2}]$)的反函数叫反正弦函数
记作$y=\arcsin x$, ($x\in [-1,1]$, $y\in [-\frac{\pi }{2},\frac{\pi }{2}]$)
或 $y=\sin$^-1$x$

注意区分: $(\sin x)$^-1=$\frac{1}{\sin x}$ \quad $\sin$^-1$x$ = $\arcsin x$

当 $x\in [-1,1]$ 时, \quad $\arcsin (-x)=-\arcsin x$
当$x\in [-\frac{\pi }{2},\frac{\pi }{2}]$时, \quad $\arcsin (\sin x)=x$
当$x\in [-1,1]$时, \quad \quad $\sin (\arcsin x)=x$

\quad
\quad

1.2反余弦函数

正弦函数 $y=\cos x$ \quad ($x\in [0,\pi ]$)的反函数叫反余弦函数
记作$y=\arccos x$, ($x\in [-1,1]$, $y\in [0,\pi ]$)
或 $y=\cos$^-1$x$

反余弦函数是严格单调递减, 有界的非奇非偶函数, 它的图像关于点(0, $\frac{\pi }{2}$)中心对称, 所以$y_1$+$y_2$= π

当$x\in [-1,1]$时, \quad $\cos$^-1(-x)$=\pi -\cos$^-1x
当 $x\in [0,\pi ]$ 时, \quad $\cos$^-1$(\cos x)=x$
当$x\in [-1,1]$时, \quad $\cos$($\cos$^-1$x$) $=x$
当$x\in [-1,1]$时, \quad $\sin$($\cos$^-1$x$) = $\sqrt{1-x^2}$

最后一个公式的证明过程
令 y=$\cos$^-1$x$ \quad $x\in [0,\pi ]$
$\sin$($\cos$^-1$x$) = $\sin y$ = $\sqrt{1-{\cos }^{2}y}$ = $\sqrt{1-x^2}$

\quad
\quad

1.3反正切函数

正切函数 $y=\tan x$ \quad ($x\in [-\frac{\pi }{2},\frac{\pi }{2}]$)的反函数叫反正切函数
记作$y=\arctan x$, ($x\in R$, $y\in [-\frac{\pi }{2},\frac{\pi }{2}]$)
或 $y=\tan$^-1$x$

当$x\in (-\infty ,\infty )$时, \quad $\arctan (-x)=-\arctan x$
当$x\in (-\frac{\pi }{2},\frac{\pi }{2})$时, \quad $\arctan (\tan x)=x$
当$x\in (-\infty ,\infty )$时, \quad $\tan (\arctan x)=x$

\quad
\quad

1.4反余切函数

余切函数 $y=\cot x$ \quad ($x\in [0,\pi ]$)的反函数叫反余切函数
记作$y=\cot$^-1x, ($x\in R$, $y\in [0,\pi ]$)

当$x\in (-\infty ,\infty )$时, \quad $\cot$^-1(-x) = π-$\cot$^-1x
当$x\in (0,\pi )$时, \quad \quad \quad $\cot$^-1($\cot x$) = $x$
当$x\in (-\infty ,\infty )$时, \quad $\cot$($\cot$^-1$x$) = $x$
当$x\in (-\infty ,0)$$\cup$(0,$\infty$)时, \quad $\tan (\cot$^-1$x$) = $\frac{1}{x}$, \quad $\cot (\tan$^-1$x$) = $\frac{1}{x}$
当$x\in (-\infty ,\infty )$时, \quad $\tan$^-1$x$ + $\cot$^-1 $x$ = $\frac{\pi }{2}$

补充
$\tan$^-1$x$ + $\cot$^-1 $x$ = $\frac{\pi }{2}$
$\sin$^-1$x$ + $\cos$^-1 $x$ = $\frac{\pi }{2}$

\quad
\quad

二.反函数

原函数 \quad 对应 \quad 反函数
y=f(x) \quad \quad \quad \quad \quad y=f^-1(x)
x \quad \quad \quad \quad \quad \quad \quad y
y \quad \quad \quad \quad \quad \quad \quad x
定义域 \quad \quad \quad \quad \quad 值域
值域 \quad \quad \quad \quad \quad 定义域

图像关于y=x轴对称,原函数与反函数单调性同增同减

求解反函数的方法
(1)把y当作常数, 将函数看作是一个方程, 求出变量x
(2)把x和y对调

\quad
\quad
例题1:

(1)$\arcsin (-1)$
$\because$-1$\in$[-1,1]
$\sin (-\frac{\pi }{2})$=-1
$\therefore$ $\arcsin (-1)$ = $-\frac{\pi }{2}$

(2)$\arcsin (-\frac{\sqrt{3}}{2})$
$\because$$-\frac{\sqrt{3}}{2}$$\in$[-1,1]
$\sin (-\frac{\pi }{3})$= $-\frac{\sqrt{3}}{2}$
$\therefore$ $\arcsin (-\frac{\sqrt{3}}{2})$ = $-\frac{\pi }{3}$

(3)$\arccos (\frac{\sqrt{2}}{2})$
$\because$ $\frac{\sqrt{2}}{2}$ $\in$[-1,1]
$\cos (\frac{\pi }{4})=\frac{\sqrt{2}}{2}$
$\therefore$ $\arccos (\frac{\sqrt{2}}{2})$ = $\frac{\pi }{4}$

(4)$\arccos 0$
$\because$ 0 $\in$[-1,1]
$\cos (\frac{\pi }{2})=0$
$\therefore$ $\arccos (0)$ = $\frac{\pi }{2}$

(5)$\arctan \frac{\sqrt{3}}{3}$
$\because$ $\frac{\sqrt{3}}{3}$ $\in$ $(-\infty ,\infty )$
$\tan \frac{\pi }{6}$ = $\frac{\sqrt{3}}{3}$
$\therefore$ $\arctan \frac{\sqrt{3}}{3}$ = $\frac{\pi }{6}$

\quad
\quad
例题2:
(1) $\sin [\arcsin (-\frac{1}{2})]$
$-\frac{1}{2}$

(2) $\arccos (\cos \frac{11\pi }{6})$
$\cos \frac{11\pi }{6}$ = $\cos (-\frac{\pi }{6})$ = $\cos (\frac{\pi }{6})$ = $\frac{\sqrt{3}}{2}$
$\therefore$ $\arccos (\frac{\sqrt{3}}{2})$ = $\frac{\pi }{6}$

\quad
\quad
例题3: 求下列函数的反函数
方法: 先求出自变量为y的方程, 再把x和y互换

(1) $y=\frac{x-1}{x+1}$
=> $y(x+1)=x-1$
=> $yx+y=x-1$
=> $yx-x=-y-1$
=> $x(y-1)=-y-1$
=> $x=\frac{-y-1}{y-1}$ 整理(上下同乘-1)
=> $x=\frac{1+y}{1-y}$
=> $y=\frac{1+x}{1-x}$

(2) $y=e$^2x
=> $\ln y=2x$
=> $x=\frac{\ln y}{2}$
=>$y=\frac{\ln x}{2}$

(3) $y=\ln (x+\sqrt{x^2+1})$
=> $e^y=x+\sqrt{x^2+1}$
=> $e^y-x=\sqrt{x^2+1}$
=> e^2y+$x^2-2x{e}^y=x^2+1$
=> e^2y$-2x{e}^y=1$
=> $e^y(e^y-2x)=1$
=> $e^y-2x=\frac{1}{e^y}$
=> $x=\frac{e^y-\frac{1}{e^y}}{2}$

(4) $y=\sin 3x$
=> $3x=\arcsin y$
=> $x=\frac{1}{3}\arcsin y$
=> $y=\frac{1}{3}\arcsin x$

(5) $y=\arcsin 3x$
=>$3x=\sin y$
=> $x=\frac{\sin y}{3}$
=> $y=\frac{1}{3}\sin x$