引言：流形的初步概念

在学习李群的时候，我们会听到的第一句话就是“李群是群，同时也是流形（Manifold）”。第一次听到流形的时候，感觉这个名字很fashion，但是又非常疑惑，到底什么东西才是流形呢？带着这样的疑惑，我参考不少教材、书本、论文以及视频，都么有得到一个快速而准确的解释。直到看到了下面这本书《A Mathematical Gift, III: The interplay between topology, functions, geometry, and algebra》（以下简称Gift），看到Kojii Shiga教授的讲解，才慢慢有了感觉。
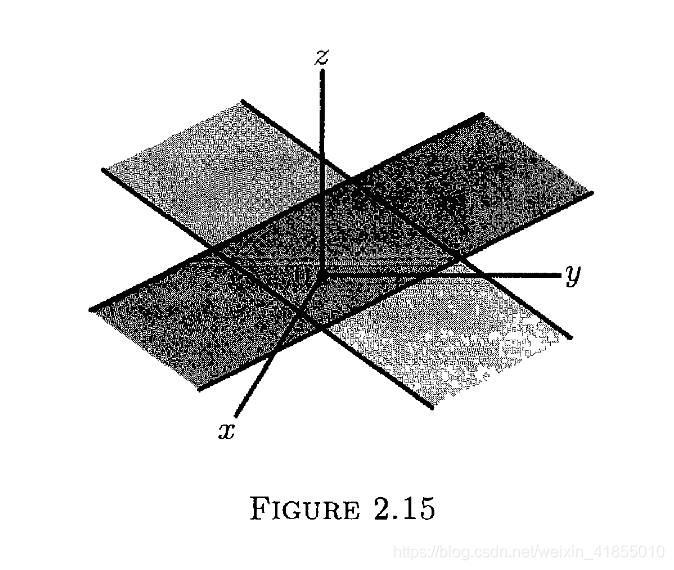
就像冯诺依曼所说的那样：“很多数学上的概念不是用来理解的，而是用来习惯的”。因为到了现代数学，很多的概念已经上升到了抽象的层面，而不仅仅停留在具体的能看得见摸得着的具象阶段。流形就是这么一个抽象的概念，如果非要用一种可视化的方式来描绘流形，我们可以引用Gift一书中的这幅图来进行展示，其中M表示n维的流形，R表示n维的欧式空间：

我们再来看流形的标准化定义。不同的地方可能描述有略微的差别，不过对于想快速了解，我们可以用一句话简单的下定义：n维流形是一种满足三大特性的集合。

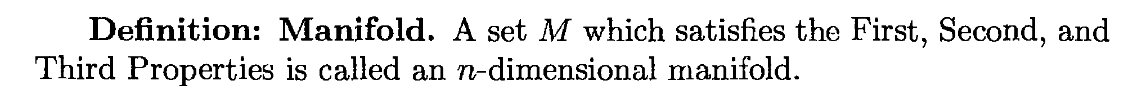
首先，在这个定义中，n维流形是一个集合，更加具体的说，它是n维点集，也就是可以使用n个独立坐标来表示的空间点，在计算机中可以使用n维数组来进行表示，更加直白的讲，它也就是n个数字。
在这里，不得不表达一下对康尔托的敬意，虽然他只是一名三流学校的教授，但是他创立的集合论无疑于是现代数学的一次革命，我们在数学和计算几种的很多概念，归根结底都是通过集合来进行定义的，或者说是集合的子类。可以说，集合对于现代数学，相当于元素周期表对于现代化学。
扯完集合我们再来看最重要的那三条性质，简单地说，就是引入领域系统的光滑拓扑空间。下面逐个来看这三条性质：

流形的性质之一：连续性

这条性质引入了“邻近/领域”的概念（英文叫做nearness，可能有其他更好的翻译），这个概念其实是用来定义连续的，领域、连续、点列、无穷级数等等的概念，其实都是数学分析的概念，因此这里是对分析的一种延续。也就是对于一个拓扑空间M，连续性是一种非常重要的性质，如果M要升级为流形，那么连续性就是一个必要的条件。
这里提到了拓扑空间，简单的说，拓扑空间就是引入了nearness的集合（点集）。拓扑空间必定是一个度量空间，也就是定义了距离的空间（点集）。有了距离之后，我们就不难理解近邻（nearness）的概念了，无非就是距离非常小，那么就认为的近邻，用数学分析里面的表达方式，我们可以使用无穷级数收敛的方法来定义点的趋近、收敛和连续。在这里需要使用到开集、开球的概念，和中学时候我们学到的开区间非常的类似。
如果无穷点序列{Pl}收敛于P，而函数f满足f(Pl)收敛于f§，那么我们认为这个函数在M上是连续的。
所以，第一条性质实际上是数学分析的延伸。核心在于距离的定义，有了距离之后，就有了邻近度的度量，然后才有了开球的概念，进而可以使用极限的办法来描述收敛，这是连续性的理论基础。

流形的性质之二：局部坐标转移性

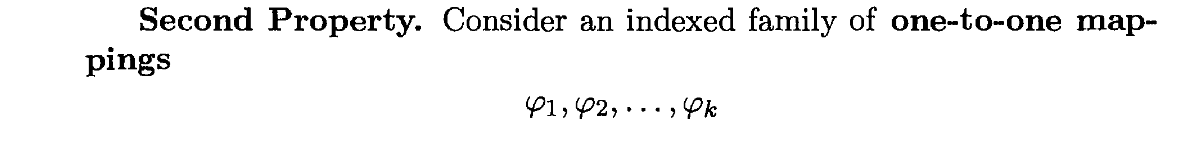
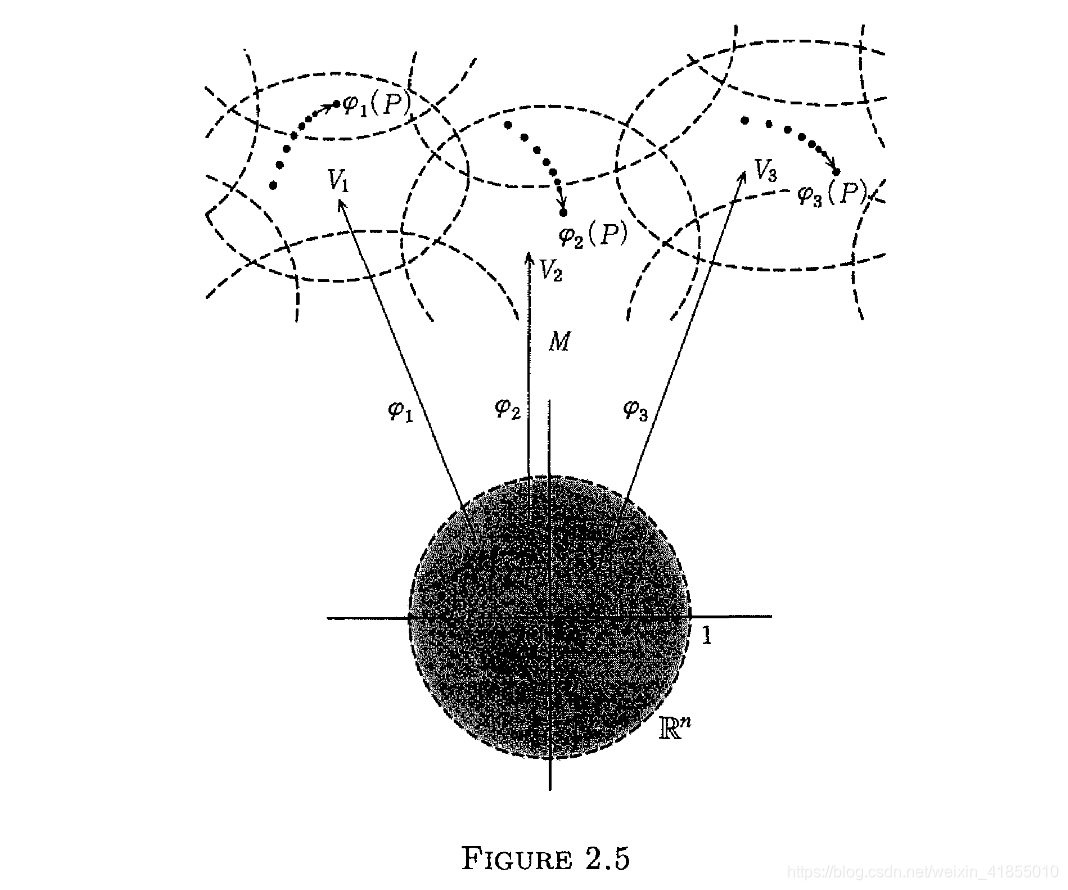
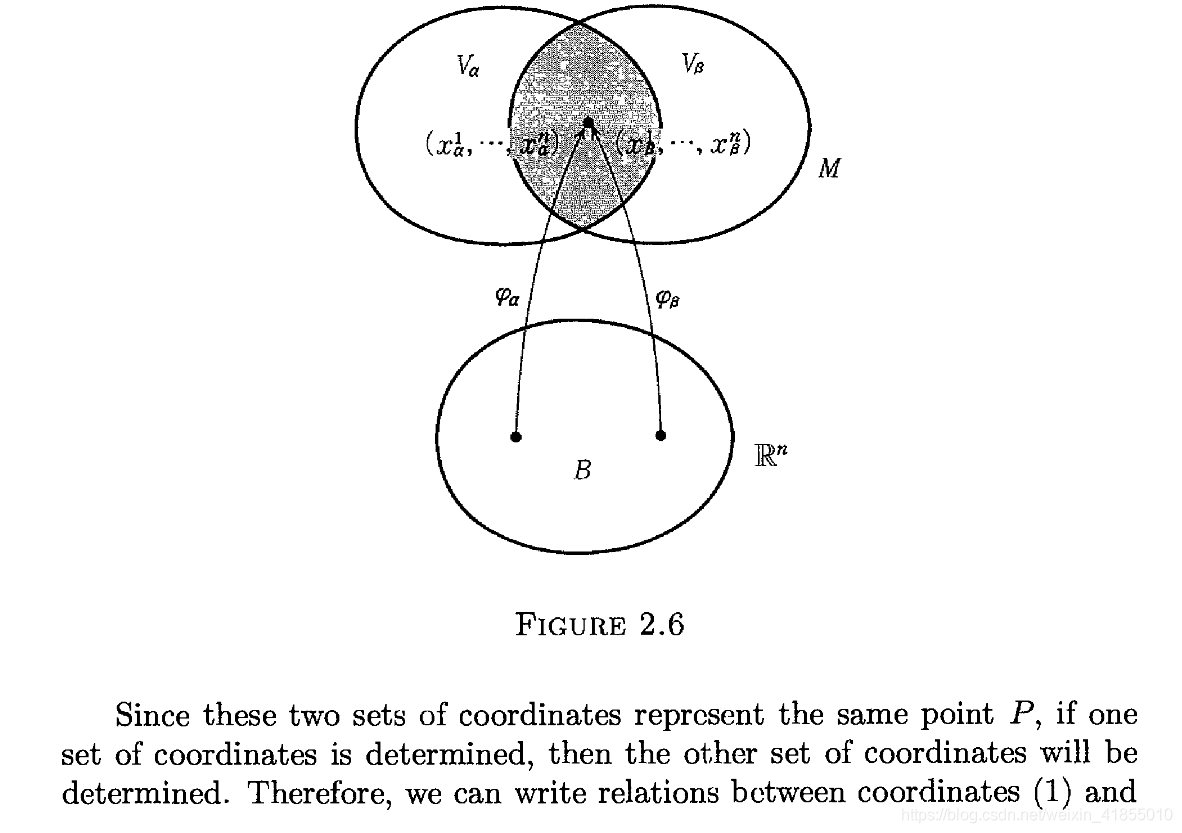
我们可以把欧式空间中的一个单位开球，通过不同的1对1映射φi到M中的不同邻域Vi里面，每个不同的Vi都具有各自的局部坐标系，如果不同的Vi产生了交集，我们就得到了坐标转移方程用来进行坐标变换。这些开集Vi的并集也是M的一个开集，这是流形需要具备的第二个特性。

流形的性质之三： 可微性

可微分性是流形的特点，与局部坐标的选择无关。我们说如果它在局部坐标系中的任何表示都是可微的，那么定义在M上的连续函数是可微的。也就是说，函数在每个局部坐标系中的所有局部表示都是可微的。在M上存在许多可微函数。

实际上，流形这个词有时用在更广义上。我们这里讨论的流形实际上叫做可微流形。流形上存在可微函数，通过对这些函数的分析，得出了流形的光滑性。在流形的研究中，可微函数起着重要的作用。

一些流形的例子

接下来我们来看一些流形的例子，便于形象生动地了解这个抽象的概念。

1.闭合曲面

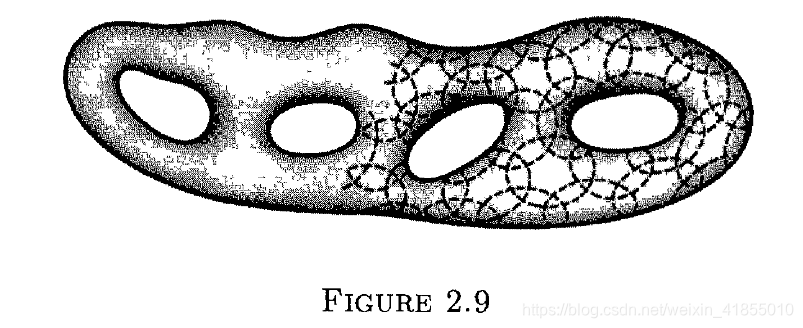
2.克莱因瓶

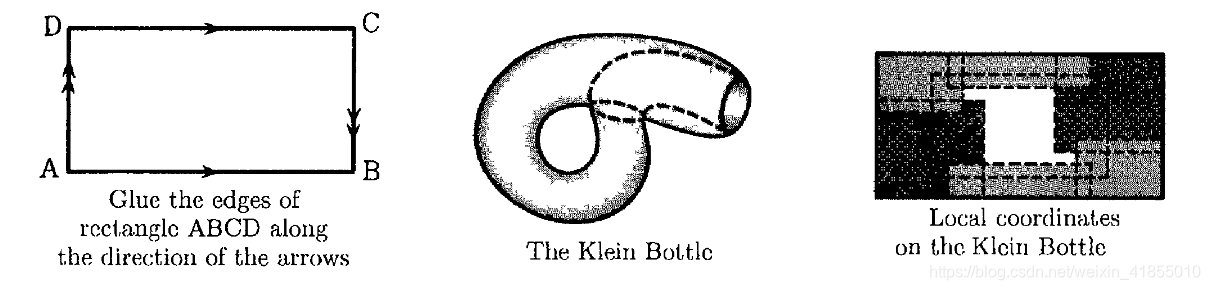
3.射影平面

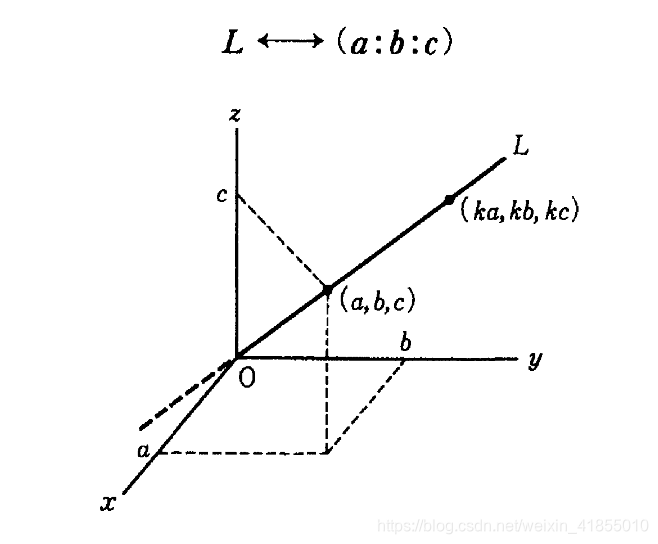
4.射影空间$P^n$

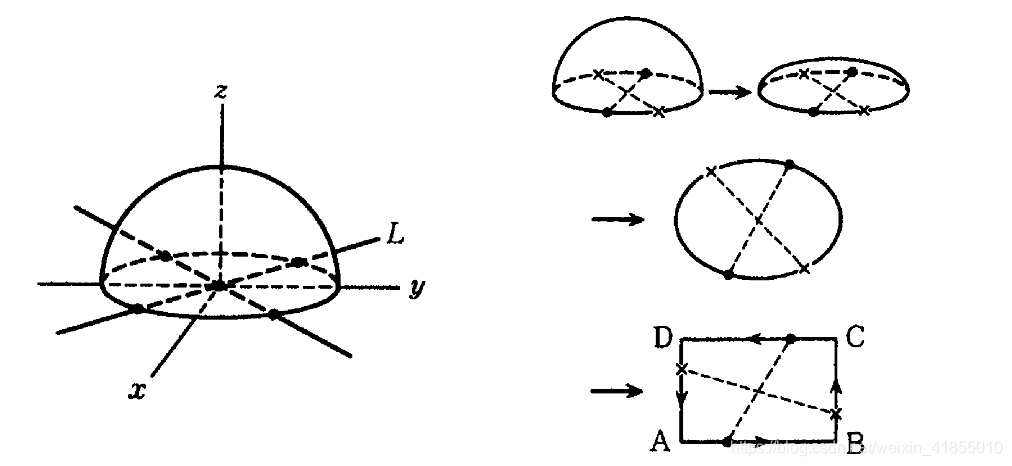
5.Grassmann流形