模式识别期末复习题
模式识别期末复习题选择感觉部分答案不对,自行判断。给不爱复习的张同学。一、判断1、影响层次聚类算法结果的主要因素有:计算模式距离的测度、聚类准则、类间距离门限、预定的类别数目。(√√√)2、欧式距离具有平移不变性和旋转不变性。(√√√)3、马式距离既具有欧式距离的特性,还具有尺度缩放不变性和不受量纲影响。(√√√)4、线性判别函数的正负和数值大小的几何意义是:正(负)表示样本点位于判别界面法向量指
模式识别期末复习题
一、判断
1、影响层次聚类算法结果的主要因素有:计算模式距离的测度、聚类准则、类间距离门限、预定的类别数目。( √ √ √)
2、欧式距离具有平移不变性和旋转不变性。( √ √ √)
3、马式距离既具有欧式距离的特性,还具有尺度缩放不变性和不受量纲影响。( √ √ √)
4、线性判别函数的正负和数值大小的几何意义是:正(负)表示样本点位于判别界面法向量指向的正(负)半空间中;绝对值正比于样本点到判别界面的距离。( √ √ √)
5、积累势函数法较之于 H — K H—K H—K 算法的优点是:该方法可用于非线性可分情况,也可用于线性可分情况。( √ √ √)
6、位势函数 K ( x , x k ) K(x,x_k) K(x,xk) 与积累位势函数 K ( x ) K(x) K(x) 的关系为 K ( x ) = ∑ x k ∈ X α k K ( x , x k ) K(x) =\sum\limits_{x_k\in X}\alpha_kK(x,x_k) K(x)=xk∈X∑αkK(x,xk) 。( √ √ √)
7、在统计模式分类问题中,聂曼-皮尔逊判决准则主要用于:某一种判决错误较另一种判决错误更为重要情况。( √ √ √)
8、“特征个数越多越有利于分类” 这种说法正确吗?( × × ×)
9、特征选择的主要目的是:从 n n n 个特征中选出最有利于分类的的 d d d 个特征( d < n d<n d<n),以降低特征维数。( √ √ √)
10、影响聚类算法结果的主要因素有:分类准则、特征选取、模式相似性测度。( √ √ √)
11、影响 C C C 均值算法的主要因素有:样本输入顺序、模式相似性测度、初始类心的选取。( √ √ √)
12、位势函数法的积累势函数 K ( x ) K(x) K(x) 的作用相当于 B a y e s Bayes Bayes 判决中的后验概率或类概率密度与先验概率的乘积,而不是先验概率和类概率密度。( √ √ √)
13、在统计模式分类问题中,当先验概率未知时,可以使用②最小最大损失准则和 N − P N-P N−P 判决而不用最小损失准则和最小误判概率准则。( √ √ √)
14、似然函数的概型已知且为单峰,则可用矩估计、最大似然估计、 B a y e s Bayes Bayes 估计、 B a y e s Bayes Bayes 学习和 P a r z e n Parzen Parzen 窗法估计该似然函数。( √ √ √)
15、从分类的角度讲,用 D K L T DKLT DKLT 做特征提取主要利用了 D K L T DKLT DKLT 的性质是:变换产生的新向量正交或不相关、 使变换后的矢量能量更趋集中。( √ √ √)
二、选择题或填空题
详细的参考教材书。
1、聚类分析算法属于(
A
A
A)
A . A. A. 无监督分类 B . B. B. 有监督分类 C . C. C. 统计模式识别方法 D . D. D. 句法模式识别方法
2、 判别域代数界面方程法属于( B B B)。
A . A. A. 无监督分类 B . B. B. 统计模式识别方法 C . C. C. 模糊模式识别方法 D . D. D. 句法模式识别方法
3、若描述模式的特征量为 0 − 1 0-1 0−1 二值特征向量,则一般采用( D D D)进行相似度量。
A . A. A. 距离测度 B . B. B. 模糊测度 C . C. C. 相似测度 D . D. D. 匹配测度
4、 下列哪个函数不作为聚类分析中的准则函数 ( B B B) 。
A . J = t r ( S ω − 1 S b ) A.J=tr({S_\omega}^{-1}S_b) A.J=tr(Sω−1Sb) B . J = ∣ S ω S b − 1 ∣ B.J=|S_\omega{S_b}^{-1}| B.J=∣SωSb−1∣
C . J = ∑ j = 1 c ∑ i = 1 N i ∣ ∣ x i ( j ) − m j ∣ ∣ 2 C.J=\sum\limits_{j=1}^{c}\sum\limits_{i=1}^{N_i}||{x_i}^{(j)}-m_j||^2 C.J=j=1∑ci=1∑Ni∣∣xi(j)−mj∣∣2 D . J = ∑ j = 1 c ( m j − m 0 ) T ( m j − m 0 ) D.J=\sum\limits_{j=1}^{c}(m_j-m_0)^T(m_j-m_0) D.J=j=1∑c(mj−m0)T(mj−m0)
5、下列判别域界面方程法中只适用于线性可分情况的算法有( A D AD AD)。
A . A. A. 感知器算法 B . B. B. H − K H-K H−K 算法 C . C. C. 积累位势函数法 D . D. D. 费歇尔线性判别法
6、线性可分、不可分都适用的有( C C C)。
A . A. A. 感知器算法 B . B. B. H − K H-K H−K 算法 C . C. C. 积累位势函数法 D . D. D. 费歇尔线性判别法
7、遗传算法的基本操作有( A A A)。
A . A. A. 复制(选择)、交叉、变异 B . B. B. 适应、交叉、变异 C . C. C. 群体、个体、变异
8、 A S O ASO ASO 算法中,信息素是( C C C)。
A . A. A. 常数 B . B. B. 随机增大 C . C. C. 有一定挥发 D . D. D. 任意变化
9、 B P BP BP 网络是( C C C)网络。
A . A. A. 单层无反馈 B . B. B. 多层有反馈 C . C. C. 多层无反馈
10、神经网络对信息的存储依赖( B B B)。
A . A. A. 神经元 B . B. B. 权系数 C . C. C. 网络节点
11、模糊均值聚类算法在求子类均值时,( B B B)参与运算。
A . A. A. 仅属于子类的样本 B . B. B. 所有样本 C . C. C. 没有样本
12、在蚁群算法中,信息素增量 Δ τ i j k ( t ) \Delta{\tau_{ij}}^k(t) Δτijk(t) 采用( A A A)时,称为蚁周系统或模型,这里, k k k 为第 k k k 只蚂蚁, Q Q Q 为常量, L k L_k Lk 为第 k k k 只蚂蚁走的路径长度, d i j d_{ij} dij 表示由 i i i 到 j j j 的边的长度。
A . A. A. Q / L k Q/L_k Q/Lk B . B. B. Q Q Q C . C. C. Q / d i j Q/d_{ij} Q/dij
三、解答题
(1)设有两类样本
ω 1 = { x 1 , x 2 } , x 1 = ( 1 , 0 , 1 ) T , x 2 = ( 0 , 1 , 1 ) T ; \omega_1=\{x_1,x_2\}, x_1 =(1,0,1)^T, x_2 =(0,1,1)^T; ω1={x1,x2},x1=(1,0,1)T,x2=(0,1,1)T;
ω 2 = { x 3 , x 4 } , x 3 = ( 1 , 1 , 0 ) T , x 4 = ( 0 , 1 , 0 ) T . \omega_2=\{x_3,x_4\},x_3=(1,1,0)^T,x_4 =(0,1,0)^T. ω2={x3,x4},x3=(1,1,0)T,x4=(0,1,0)T.
试用感知器算法,求出其分类用的线性判别函数。
解:增广规范化: x 1 = ( 1 , 0 , 1 , 1 ) T , x 2 = ( 0 , 1 , 1 , 1 ) T , x 3 = ( − 1 , − 1 , 0 , − 1 ) T , x 4 = ( 0 , − 1 , 0 , − 1 ) T x_1=(1,0,1,1)^T,x_2=(0,1,1,1)^T,x_3=(-1,-1,0,-1)^T,x_4=(0,-1,0,-1)^T x1=(1,0,1,1)T,x2=(0,1,1,1)T,x3=(−1,−1,0,−1)T,x4=(0,−1,0,−1)T,
设 W 1 = ( 1 , 1 , 1 , 1 ) T , c = 1 W_1=(1,1,1,1)^T,c=1 W1=(1,1,1,1)T,c=1
W 1 T x 1 = 3 > 0 {W_1}^Tx_1=3>0 W1Tx1=3>0
W 1 T x 2 = 3 > 0 {W_1}^Tx_2=3>0 W1Tx2=3>0
W 1 T x 3 = − 3 < 0 {W_1}^Tx_3=-3<0 W1Tx3=−3<0 修正
W 2 = W 1 + x 3 = ( 0 , 0 , 1 , 0 ) T W_2=W_1+x_3=(0,0,1,0)^T W2=W1+x3=(0,0,1,0)T
W 2 T x 4 = 0 {W_2}^Tx_4=0 W2Tx4=0 修正
W 3 = W 2 + x 4 = ( 0 , − 1 , 1 , − 1 ) T W_3=W_2+x_4=(0,-1,1,-1)^T W3=W2+x4=(0,−1,1,−1)T
W 3 T x 1 = 0 {W_3}^Tx_1=0 W3Tx1=0 修正
W 4 = W 3 + x 1 = ( 1 , − 1 , 2 , 0 ) T W_4=W_3+x_1=(1,-1,2,0)^T W4=W3+x1=(1,−1,2,0)T
W 4 T x 3 = 0 {W_4}^Tx_3=0 W4Tx3=0 修正
W 5 = W 4 + x 3 = ( 0 , − 2 , 2 , − 1 ) T W_5=W_4+x_3=(0,-2,2,-1)^T W5=W4+x3=(0,−2,2,−1)T
W 5 T x 2 = − 3 < 0 {W_5}^Tx_2=-3<0 W5Tx2=−3<0 修正
W 6 = W 5 + x 2 = ( 0 , − 1 , 3 , 0 ) T W_6=W_5+x_2=(0,-1,3,0)^T W6=W5+x2=(0,−1,3,0)T
训练结束, W = W 6 = ( 0 , − 1 , 3 , 0 ) W=W_6=(0,-1,3,0) W=W6=(0,−1,3,0)
线性判别函数为 d ( X ) = W T X = − x 2 + 3 X 3 d(X)=W^TX=-x_2+3X_3 d(X)=WTX=−x2+3X3
(2)已知有两类数据,分别为 ω 1 : ( 1 , 0 ) T , ( 2 , 0 ) T , ( 1 , 1 ) T ; ω 2 : ( − 1 , 0 ) T , ( 0 , 1 ) T , ( − 1 , 1 ) T \omega_1:(1,0)^T,(2,0)^T,(1,1)^T;\omega_2:(-1,0)^T,(0,1)^T,(-1,1)^T ω1:(1,0)T,(2,0)T,(1,1)T;ω2:(−1,0)T,(0,1)T,(−1,1)T
试求:该组数据的类内及类间离散矩阵 S ω S_\omega Sω 及 S b S_b Sb 。
解: m 1 = ( 4 3 , 1 3 ) T , m 2 = ( − 2 3 , 2 3 ) T m_1=(\frac{4}{3},\frac{1}{3})^T,m_2=(-\frac{2}{3},\frac{2}{3})^T m1=(34,31)T,m2=(−32,32)T
S 1 = ∑ x ∈ ω 1 ( x − m 1 ) ( x − m 1 ) T = ( 2 3 − 1 3 − 1 3 2 3 ) S_1=\sum\limits_{x\in \omega_1}(x-m_1)(x-m_1)^T=\left(\begin{matrix}\frac{2}{3}&-\frac{1}{3}\\-\frac{1}{3}&\frac{2}{3}\end{matrix}\right) S1=x∈ω1∑(x−m1)(x−m1)T=(32−31−3132),
S 2 = ∑ x ∈ ω 2 ( x − m 2 ) ( x − m 2 ) T = ( 2 3 1 3 1 3 2 3 ) S_2=\sum\limits_{x\in \omega_2}(x-m_2)(x-m_2)^T=\left(\begin{matrix}\frac{2}{3}&\frac{1}{3}\\\frac{1}{3}&\frac{2}{3}\end{matrix}\right) S2=x∈ω2∑(x−m2)(x−m2)T=(32313132),
S ω = 1 2 ( S 1 + S 2 ) = ( 2 3 0 0 2 3 ) S_\omega=\frac{1}{2}(S_1+S_2)=\left(\begin{matrix}\frac{2}{3}&0\\0&\frac{2}{3}\end{matrix}\right) Sω=21(S1+S2)=(320032),
S b = ( m 1 − m 2 ) ( m 1 − m 2 ) T = ( 2 − 1 3 ) ( 2 − 1 3 ) = ( 4 − 2 3 − 2 3 1 9 ) S_b=(m_1-m_2)(m_1-m_2)^T=\left(\begin{matrix}2\\-\frac{1}{3}\end{matrix}\right)\left(\begin{matrix}2&-\frac{1}{3}\end{matrix}\right)=\left(\begin{matrix}4&-\frac{2}{3}\\-\frac{2}{3}&\frac{1}{9}\end{matrix}\right) Sb=(m1−m2)(m1−m2)T=(2−31)(2−31)=(4−32−3291)。
(3)设有两类样本: ω 1 = { ( 0 , 0 ) T , ( 0 , 1 ) T } , ω 2 = { ( 1 , 0 ) T , ( 1 , 1 ) T } . \omega_1 =\{(0,0)^T,(0,1)^T\}, \omega_2 =\{(1,0)^T,(1,1)^T\}. ω1={(0,0)T,(0,1)T},ω2={(1,0)T,(1,1)T}.
试画出何-卡氏算法求其线性判别函数的流程图,并求出该函数。
解:
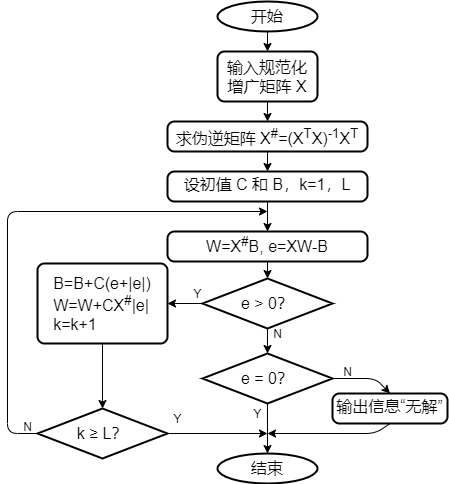
X = ( 0 0 1 0 1 1 − 1 0 − 1 − 1 − 1 − 1 ) , X # = ( X T X ) − 1 X T = 1 4 ( − 2 − 2 − 2 − 2 − 2 2 2 − 2 3 1 − 1 1 ) X=\left(\begin{matrix}0&0&1\\0&1&1\\-1&0&-1\\-1&-1&-1\end{matrix}\right),X^\#=(X^TX)^{-1}X^T=\frac{1}{4}\left(\begin{matrix}-2&-2&-2&-2\\-2&2&2&-2\\3&1&-1&1\end{matrix}\right) X=⎝⎜⎜⎛00−1−1010−111−1−1⎠⎟⎟⎞,X#=(XTX)−1XT=41⎝⎛−2−23−221−22−1−2−21⎠⎞,
取 校正增量 c = 1 c=1 c=1,迭代次数 k = 1 , B 1 = ( 1 , 1 , 1 , 1 ) T k=1,B_1=(1,1,1,1)^T k=1,B1=(1,1,1,1)T,
W 1 = X # B 1 = ( − 2 , 0 , 1 ) T W_1=X^\#B_1=(-2,0,1)^T W1=X#B1=(−2,0,1)T,
e 1 = X W 1 − B 1 = ( 0 0 0 0 ) = 0 → e_1=XW_1-B_1=\left(\begin{matrix}0\\0\\0\\0\end{matrix}\right)=\overrightarrow{0} e1=XW1−B1=⎝⎜⎜⎛0000⎠⎟⎟⎞=0,
所以 W 1 W_1 W1 为所求解,系统线性可分,判别函数 d ( X ) = W T ( x 1 , x 2 , 1 ) T = − 2 x 1 + 1 d(X)=W^T(x_1,x_2,1)^T=-2x_1+1 d(X)=WT(x1,x2,1)T=−2x1+1。
(4)有训练集资料矩阵如下表所示,现已知, N = 9 , N 1 = N 2 = N 3 = 3 , n = 2 , M = 3 N=9,N_1=N_2=N_3=3,n=2,M=3 N=9,N1=N2=N3=3,n=2,M=3。
| 训练样本号k | 1 2 3 | 1 2 3 | 1 2 3 |
|---|---|---|---|
| 特征 x 1 x_1 x1 | 0 1 2 | -2 -1 -2 | 0 1 -1 |
| 特征 x 2 x_2 x2 | 1 -1 1 | 1 0 -1 | -1 -2 -2 |
| 类别 | ω 1 \omega_1 ω1 | ω 2 \omega_2 ω2 | ω 3 \omega_3 ω3 |
假定三类协方差不等,每一类都符合正态分布,
先验概率 P ( ω 1 ) = P ( ω 2 ) = P ( ω 3 ) = 1 3 P(\omega_1)=P(\omega_2)=P(\omega_3)=\frac{1}{3} P(ω1)=P(ω2)=P(ω3)=31,
多类判别函数 g i ( X ) = X T W i X + ω i T X + ω i 0 g_i(X)=X^TW_iX+{\omega_i}^TX+\omega_{i0} gi(X)=XTWiX+ωiTX+ωi0,
其中, W i = − 1 2 ∑ i − 1 , ω i = ∑ i − 1 μ i , ω i 0 = − 1 2 μ i T ∑ i − 1 μ i − 1 2 ln ∣ ∑ i ∣ + ln P ( ω i ) W_i=-\frac{1}{2}{\sum_{i}}^{-1},\omega_i={\sum_{i}}^{-1}\mu_i,\omega_{i0}=-\frac{1}{2}{\mu_i}^T{\sum_{i}}^{-1}\mu_i-\frac{1}{2}\ln|\sum_i|+\ln P(\omega_i) Wi=−21∑i−1,ωi=∑i−1μi,ωi0=−21μiT∑i−1μi−21ln∣∑i∣+lnP(ωi)。
试先求出每一类的判别函数,然后判断未知样本 x = ( 1 , 1 ) T x=(1,1)^T x=(1,1)T 应属于哪一类?
解: μ 1 = ( 1 , 1 3 ) T , μ 2 = ( − 5 3 , 0 ) T , μ 3 = ( 0 , − 5 3 ) T \mu_1=(1,\frac{1}{3})^T,\mu_2=(-\frac{5}{3},0)^T,\mu_3=(0,-\frac{5}{3})^T μ1=(1,31)T,μ2=(−35,0)T,μ3=(0,−35)T,
∑ 1 = 1 3 − 1 [ ( − 1 2 3 ) ( − 1 2 3 ) + ( 0 − 4 3 ) ( 0 − 4 3 ) + ( 1 2 3 ) ( 1 2 3 ) ] = ( 1 0 0 4 3 ) \sum_1=\frac{1}{3-1}[\left(\begin{matrix}-1\\\frac{2}{3}\end{matrix}\right)(-1 \frac{2}{3})+\left(\begin{matrix}0\\-\frac{4}{3}\end{matrix}\right)(0 -\frac{4}{3})+\left(\begin{matrix}1\\\frac{2}{3}\end{matrix}\right)(1 \frac{2}{3})]=\left(\begin{matrix}1&0\\0&\frac{4}{3}\end{matrix}\right) ∑1=3−11[(−132)(−1 32)+(0−34)(0 −34)+(132)(1 32)]=(10034),
∑ 2 = 1 3 − 1 [ ( − 1 3 1 ) ( − 1 3 1 ) + ( 2 3 0 ) ( 2 3 0 ) + ( − 1 3 − 1 ) ( − 1 3 − 1 ) ] = ( 1 3 0 0 1 ) \sum_2=\frac{1}{3-1}[\left(\begin{matrix}-\frac{1}{3}\\1\end{matrix}\right)(-\frac{1}{3} 1)+\left(\begin{matrix}\frac{2}{3}\\0\end{matrix}\right)(\frac{2}{3} 0)+\left(\begin{matrix}-\frac{1}{3}\\-1\end{matrix}\right)(-\frac{1}{3} -1)]=\left(\begin{matrix}\frac{1}{3}&0\\0&1\end{matrix}\right) ∑2=3−11[(−311)(−31 1)+(320)(32 0)+(−31−1)(−31 −1)]=(31001),
∑ 3 = 1 3 − 1 [ ( 0 2 3 ) ( 0 2 3 ) + ( 1 − 1 3 ) ( 1 − 1 3 ) + ( − 1 − 1 3 ) ( − 1 − 1 3 ) ] = ( 1 0 0 1 3 ) \sum_3=\frac{1}{3-1}[\left(\begin{matrix}0\\\frac{2}{3}\end{matrix}\right)(0 \frac{2}{3})+\left(\begin{matrix}1\\-\frac{1}{3}\end{matrix}\right)(1 -\frac{1}{3})+\left(\begin{matrix}-1\\-\frac{1}{3}\end{matrix}\right)(-1 -\frac{1}{3})]=\left(\begin{matrix}1&0\\0&\frac{1}{3}\end{matrix}\right) ∑3=3−11[(032)(0 32)+(1−31)(1 −31)+(−1−31)(−1 −31)]=(10031),
g 1 ( X ) = X T W 1 X + ω 1 T X + ω 10 = − 1 2 ( x 1 2 + 3 4 x 2 2 ) + x 1 + 1 4 x 2 − 1.7841 g_1(X)=X^TW_1X+{\omega_1}^TX+\omega_{10}=-\frac{1}{2}({x_1}^2+\frac{3}{4}{x_2}^2)+x_1+\frac{1}{4}x_2-1.7841 g1(X)=XTW1X+ω1TX+ω10=−21(x12+43x22)+x1+41x2−1.7841,
g 2 ( X ) = X T W 2 X + ω 2 T X + ω 20 = − 1 2 ( 3 x 1 2 + x 2 2 ) − 5 x 1 − 5.2653 g_2(X)=X^TW_2X+{\omega_2}^TX+\omega_{20}=-\frac{1}{2}(3{x_1}^2+{x_2}^2)-5x_1-5.2653 g2(X)=XTW2X+ω2TX+ω20=−21(3x12+x22)−5x1−5.2653,
g 3 ( X ) = X T W 3 X + ω 3 T X + ω 30 = − 1 2 ( x 1 2 + 3 x 2 2 ) + x 1 − 5 3 x 2 − 4.176 g_3(X)=X^TW_3X+{\omega_3}^TX+\omega_{30}=-\frac{1}{2}({x_1}^2+3{x_2}^2)+x_1-\frac{5}{3}x_2-4.176 g3(X)=XTW3X+ω3TX+ω30=−21(x12+3x22)+x1−35x2−4.176,
将 x = ( 1 , 1 ) T x=(1,1)^T x=(1,1)T 代入, g 1 ( x ) = − 1.4091 , g 2 ( x ) = − 12.2653 , g 3 ( x ) = − 11.7160 g_1(x)=-1.4091,g_2(x)=-12.2653,g_3(x)=-11.7160 g1(x)=−1.4091,g2(x)=−12.2653,g3(x)=−11.7160,
g 1 ( x ) g_1(x) g1(x) 最大,判 x = ( 1 , 1 ) T ∈ ω 1 x=(1,1)^T\in \omega_1 x=(1,1)T∈ω1。
(5)已知正常细胞先验概率为 P ( ω 1 ) = 0.9 P(\omega_1)=0.9 P(ω1)=0.9, 异常为 P ( ω 2 ) = 0.1 P(\omega_2)=0.1 P(ω2)=0.1,
从类条件概率密度分布曲线上查的 p ( x ∣ ω 1 ) = 0.3 , p ( x ∣ ω 2 ) = 0.5 , λ 11 = 0 , λ 21 = 7 , λ 12 = 2 , λ 22 = 0 p(x|\omega_1)=0.3,p(x|\omega_2)=0.5,\lambda_{11}=0,\lambda_{21}=7,\lambda_{12}=2,\lambda_{22}=0 p(x∣ω1)=0.3,p(x∣ω2)=0.5,λ11=0,λ21=7,λ12=2,λ22=0
条件风险: R ( ω i ∣ x ) = ∑ j = 1 2 λ i j P ( ω j ∣ x ) R(\omega_i|x)=\sum\limits_{j=1}^{2}\lambda_{ij}P(\omega_j|x) R(ωi∣x)=j=1∑2λijP(ωj∣x),
试按条件风险最小来决定 x x x 所属的类别。
解: P ( x ) = P ( x ∣ ω 1 ) P ( ω 1 ) + P ( x ∣ ω 2 ) P ( ω 2 ) = 0.27 + 0.05 = 0.32 P(x)=P(x|\omega_1)P(\omega_1)+P(x|\omega_2)P(\omega_2)=0.27+0.05=0.32 P(x)=P(x∣ω1)P(ω1)+P(x∣ω2)P(ω2)=0.27+0.05=0.32,
P ( ω 1 ∣ x ) = P ( x ∣ ω 1 ) P ( ω 1 ) P ( x ) = 0.844 P(\omega_1|x)=\frac{P(x|\omega_1)P(\omega_1)}{P(x)}=0.844 P(ω1∣x)=P(x)P(x∣ω1)P(ω1)=0.844,
P ( ω 2 ∣ x ) = P ( x ∣ ω 2 ) P ( ω 2 ) P ( x ) = 0.156 P(\omega_2|x)=\frac{P(x|\omega_2)P(\omega_2)}{P(x)}= 0.156 P(ω2∣x)=P(x)P(x∣ω2)P(ω2)=0.156,
R ( ω 1 ∣ x ) = 0 + 2 ∗ 0.156 = 0.312 R(\omega_1|x)=0+2*0.156=0.312 R(ω1∣x)=0+2∗0.156=0.312,
R ( ω 2 ∣ x ) = 7 ∗ 0.844 + 0 = 5.908 R(\omega_2|x)=7*0.844+0=5.908 R(ω2∣x)=7∗0.844+0=5.908。
所以,按条件风险最小的原则, x x x 应判为属于第一类。
(6)设两个集群的数据分别为 ( 1 , 0 ) T , ( 2 , 0 ) T , ( 1 , 1 ) T {(1,0)^T,(2,0)^T,(1,1)^T} (1,0)T,(2,0)T,(1,1)T与 ( 0 , 1 ) T , ( − 1 , 0 ) T , ( − 1 , 1 ) T {(0,1)^T,(-1,0)^T,(-1,1)^T} (0,1)T,(−1,0)T,(−1,1)T。
试求:
1) 两个集群的均值。
2) 若将数据 ( 1 , 1 ) T (1,1)^T (1,1)T 从第一个集群转移至第二个集群时,准则函数值 J J J (每个样本与其所在集群均值点的距离平方和)的变化量。
解:
1) m 1 = ( 4 3 , 1 3 ) T , m 2 = ( − 2 3 , 2 3 ) T m_1=(\frac{4}{3},\frac{1}{3})^T,m_2=(-\frac{2}{3},\frac{2}{3})^T m1=(34,31)T,m2=(−32,32)T。
2) J 0 = ∑ i = 1 c ∑ x ∈ ω i ∣ ∣ x − m i ∣ ∣ 2 \begin{aligned}J_0&=\sum\limits_{i=1}^{c}\sum\limits_{x\in \omega_i}{||x-m_i||}^2\end{aligned} J0=i=1∑cx∈ωi∑∣∣x−mi∣∣2, c c c 为类数。
( 1 , 1 ) T (1,1)^T (1,1)T 从第一个集群中移出,准则函数值减少为 3 3 − 1 ∣ ∣ ( 1 , 1 ) T − ( 4 3 , 1 3 ) T ∣ ∣ 2 = 5 6 \frac{3}{3-1}||(1,1)^T-(\frac{4}{3},\frac{1}{3})^T||^2=\frac{5}{6} 3−13∣∣(1,1)T−(34,31)T∣∣2=65,
该数据加入第二个集群,准则函数值增加为 3 3 + 1 ∣ ∣ ( 1 , 1 ) T − ( − 2 3 , 2 3 ) T ∣ ∣ 2 = 13 6 \frac{3}{3+1}||(1,1)^T-(-\frac{2}{3},\frac{2}{3})^T||^2=\frac{13}{6} 3+13∣∣(1,1)T−(−32,32)T∣∣2=613。
准则函数值增加量为 4 3 \frac{4}{3} 34,不宜转。
(7)若数据集共有 m m m 个类 ω 1 , ω 2 , ⋅ ⋅ ⋅ , ω m \omega_1,\omega_2,···,\omega_m ω1,ω2,⋅⋅⋅,ωm,总离散矩阵为 S ω S_\omega Sω
1 ) 试求证某一数据 x x x 从 ω i \omega_i ωi 转移至 ω j \omega_j ωj 类时, ω i \omega_i ωi 的散布矩阵的变化量为 − N i N i − 1 ( x − m i ) ( x − m i ) T -\frac{N_i}{N_i-1}(x-m_i)(x-m_i)^T −Ni−1Ni(x−mi)(x−mi)T 其中 m i m_i mi 是转移前类 τ i \tau_i τi 的均值向量, N i N_i Ni 是转移前 ω i \omega_i ωi 的数据量。
2)推测 ω j \omega_j ωj 在增加数据 x x x 后其散布矩阵的变化量。
3)计算总散布矩阵的变化量。
解:
m i ′ = 1 N i − 1 ( m i ∗ N i − x ) = 1 N i − 1 [ ( N i − 1 ) m i + m i − x ] = m i + 1 N i − 1 ( m i − x ) \begin{aligned}{m_i}^{'}&=\frac{1}{N_i-1}(m_i*N_i-x)=\frac{1}{N_i-1}[(N_i-1)m_i+m_i-x]\\&=m_i+\frac{1}{N_i-1}(m_i-x)\end{aligned} mi′=Ni−11(mi∗Ni−x)=Ni−11[(Ni−1)mi+mi−x]=mi+Ni−11(mi−x)
按离散矩阵的定义计算,可得 τ i \tau_i τi 的离散矩阵变化前后的关系为:
S i ′ = S i − N i N i − 1 ( x − m i ) ( x − m i ) T {S_i}^{'}=S_i-\frac{N_i}{N_i-1}(x-m_i)(x-m_i)^T Si′=Si−Ni−1Ni(x−mi)(x−mi)T,
2)同理,可计算 τ j \tau_j τj 的离散矩阵变化前后的关系为:
S j ′ = S j + N i N i − 1 ( x − m j ) ( x − m j ) T {S_j}^{'}=S_j+\frac{N_i}{N_i-1}(x-m_j)(x-m_j)^T Sj′=Sj+Ni−1Ni(x−mj)(x−mj)T,
3)故总的离散矩阵变化前后的关系为:
S ω ′ = S ω − N i N i − 1 ( x − m i ) ( x − m i ) T + N j N j − 1 ( x − m j ) ( x − m j ) T {S_\omega}^{'}=S_\omega-\frac{N_i}{N_i-1}(x-m_i)(x-m_i)^T+\frac{N_j}{N_j-1}(x-m_j)(x-m_j)^T Sω′=Sω−Ni−1Ni(x−mi)(x−mi)T+Nj−1Nj(x−mj)(x−mj)T。
(8)已知有 5 5 5 个样本,每个样本有 2 2 2 个特征,类型数目 M = 2 M=2 M=2,数据如下:
| 样本序号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 特征 x 1 x_1 x1 | 0 | 1 | 3 | 6 | 7 |
| 特征 x 2 x_2 x2 | 0 | 0 | 2 | 6 | 6 |
试用 K − K- K−均值算法找聚类中心,并对它们进行聚类。
解:先设 Z 1 ( 1 ) = ( 0 , 0 ) T , Z 2 ( 1 ) = ( 1 , 0 ) T Z_1(1)=(0,0)^T,Z_2(1)=(1,0)^T Z1(1)=(0,0)T,Z2(1)=(1,0)T,
∣ ∣ x 3 − Z 1 ( 1 ) ∣ ∣ > ∣ ∣ x 3 − Z 2 ( 1 ) ∣ ∣ ||x_3-Z_1(1)||>||x_3-Z_2(1)|| ∣∣x3−Z1(1)∣∣>∣∣x3−Z2(1)∣∣,
∣ ∣ x 4 − Z 1 ( 1 ) ∣ ∣ > ∣ ∣ x 4 − Z 2 ( 1 ) ∣ ∣ ||x_4-Z_1(1)||>||x_4-Z_2(1)|| ∣∣x4−Z1(1)∣∣>∣∣x4−Z2(1)∣∣,
∣ ∣ x 5 − Z 1 ( 1 ) ∣ ∣ > ∣ ∣ x 5 − Z 2 ( 1 ) ∣ ∣ ||x_5-Z_1(1)||>||x_5-Z_2(1)|| ∣∣x5−Z1(1)∣∣>∣∣x5−Z2(1)∣∣,
分为两类 ω 1 : x 1 ; ω 2 : x 2 , x 3 , x 4 , x 5 \omega_1:x_1;\omega_2:x_2,x_3,x_4,x_5 ω1:x1;ω2:x2,x3,x4,x5
Z 1 ( 2 ) = ( 0 , 0 ) T , Z 2 ( 2 ) = ( 17 4 , 7 2 ) T Z_1(2)=(0,0)^T,Z_2(2)=(\frac{17}{4},\frac{7}{2})^T Z1(2)=(0,0)T,Z2(2)=(417,27)T,
∣ ∣ x 1 − Z 1 ( 2 ) ∣ ∣ < ∣ ∣ x 1 − Z 2 ( 2 ) ∣ ∣ ||x_1-Z_1(2)||<||x_1-Z_2(2)|| ∣∣x1−Z1(2)∣∣<∣∣x1−Z2(2)∣∣,
∣ ∣ x 2 − Z 1 ( 2 ) ∣ ∣ < ∣ ∣ x 2 − Z 2 ( 2 ) ∣ ∣ ||x_2-Z_1(2)||<||x_2-Z_2(2)|| ∣∣x2−Z1(2)∣∣<∣∣x2−Z2(2)∣∣,
∣ ∣ x 3 − Z 1 ( 2 ) ∣ ∣ > ∣ ∣ x 3 − Z 2 ( 2 ) ∣ ∣ ||x_3-Z_1(2)||>||x_3-Z_2(2)|| ∣∣x3−Z1(2)∣∣>∣∣x3−Z2(2)∣∣,
∣ ∣ x 4 − Z 1 ( 2 ) ∣ ∣ > ∣ ∣ x 4 − Z 2 ( 2 ) ∣ ∣ ||x_4-Z_1(2)||>||x_4-Z_2(2)|| ∣∣x4−Z1(2)∣∣>∣∣x4−Z2(2)∣∣,
∣ ∣ x 5 − Z 1 ( 2 ) ∣ ∣ > ∣ ∣ x 5 − Z 2 ( 2 ) ∣ ∣ ||x_5-Z_1(2)||>||x_5-Z_2(2)|| ∣∣x5−Z1(2)∣∣>∣∣x5−Z2(2)∣∣,
分为两类 ω 1 : x 1 , x 2 ; ω 2 : x 3 , x 4 , x 5 \omega_1:x_1,x_2;\omega_2:x_3,x_4,x_5 ω1:x1,x2;ω2:x3,x4,x5
Z 1 ( 3 ) = ( 1 2 , 0 ) T , Z 2 ( 3 ) = ( 16 3 , 14 3 ) T Z_1(3)=(\frac{1}{2},0)^T,Z_2(3)=(\frac{16}{3},\frac{14}{3})^T Z1(3)=(21,0)T,Z2(3)=(316,314)T,
∣ ∣ x 1 − Z 1 ( 3 ) ∣ ∣ < ∣ ∣ x 1 − Z 2 ( 3 ) ∣ ∣ ||x_1-Z_1(3)||<||x_1-Z_2(3)|| ∣∣x1−Z1(3)∣∣<∣∣x1−Z2(3)∣∣,
∣ ∣ x 2 − Z 1 ( 3 ) ∣ ∣ < ∣ ∣ x 2 − Z 2 ( 3 ) ∣ ∣ ||x_2-Z_1(3)||<||x_2-Z_2(3)|| ∣∣x2−Z1(3)∣∣<∣∣x2−Z2(3)∣∣,
∣ ∣ x 3 − Z 1 ( 3 ) ∣ ∣ < ∣ ∣ x 3 − Z 2 ( 3 ) ∣ ∣ ||x_3-Z_1(3)||<||x_3-Z_2(3)|| ∣∣x3−Z1(3)∣∣<∣∣x3−Z2(3)∣∣,
∣ ∣ x 4 − Z 1 ( 3 ) ∣ ∣ > ∣ ∣ x 4 − Z 2 ( 3 ) ∣ ∣ ||x_4-Z_1(3)||>||x_4-Z_2(3)|| ∣∣x4−Z1(3)∣∣>∣∣x4−Z2(3)∣∣,
∣ ∣ x 5 − Z 1 ( 3 ) ∣ ∣ > ∣ ∣ x 5 − Z 2 ( 3 ) ∣ ∣ ||x_5-Z_1(3)||>||x_5-Z_2(3)|| ∣∣x5−Z1(3)∣∣>∣∣x5−Z2(3)∣∣,
分为两类 ω 1 : x 1 , x 2 , x 3 ; ω 2 : x 4 , x 5 \omega_1:x_1,x_2,x_3;\omega_2:x_4,x_5 ω1:x1,x2,x3;ω2:x4,x5
Z 1 ( 4 ) = ( 4 3 , 2 3 ) T , Z 2 ( 4 ) = ( 13 2 , 6 ) T Z_1(4)=(\frac{4}{3},\frac{2}{3})^T,Z_2(4)=(\frac{13}{2},6)^T Z1(4)=(34,32)T,Z2(4)=(213,6)T,
∣ ∣ x 1 − Z 1 ( 4 ) ∣ ∣ < ∣ ∣ x 1 − Z 2 ( 4 ) ∣ ∣ ||x_1-Z_1(4)||<||x_1-Z_2(4)|| ∣∣x1−Z1(4)∣∣<∣∣x1−Z2(4)∣∣,
∣ ∣ x 2 − Z 1 ( 4 ) ∣ ∣ < ∣ ∣ x 2 − Z 2 ( 4 ) ∣ ∣ ||x_2-Z_1(4)||<||x_2-Z_2(4)|| ∣∣x2−Z1(4)∣∣<∣∣x2−Z2(4)∣∣,
∣ ∣ x 3 − Z 1 ( 4 ) ∣ ∣ < ∣ ∣ x 3 − Z 2 ( 4 ) ∣ ∣ ||x_3-Z_1(4)||<||x_3-Z_2(4)|| ∣∣x3−Z1(4)∣∣<∣∣x3−Z2(4)∣∣,
∣ ∣ x 4 − Z 1 ( 4 ) ∣ ∣ > ∣ ∣ x 4 − Z 2 ( 4 ) ∣ ∣ ||x_4-Z_1(4)||>||x_4-Z_2(4)|| ∣∣x4−Z1(4)∣∣>∣∣x4−Z2(4)∣∣,
∣ ∣ x 5 − Z 1 ( 4 ) ∣ ∣ > ∣ ∣ x 5 − Z 2 ( 4 ) ∣ ∣ ||x_5-Z_1(4)||>||x_5-Z_2(4)|| ∣∣x5−Z1(4)∣∣>∣∣x5−Z2(4)∣∣,
分为两类 ω 1 : x 1 , x 2 , x 3 ; ω 2 : x 4 , x 5 \omega_1:x_1,x_2,x_3;\omega_2:x_4,x_5 ω1:x1,x2,x3;ω2:x4,x5
Z 1 ( 5 ) = ( 4 3 , 2 3 ) T , Z 2 ( 5 ) = ( 13 2 , 6 ) T , Z 1 ( 5 ) = Z 1 ( 4 ) , Z 2 ( 5 ) = Z 2 ( 4 ) Z_1(5)=(\frac{4}{3},\frac{2}{3})^T,Z_2(5)=(\frac{13}{2},6)^T,Z_1(5)=Z_1(4),Z_2(5)=Z_2(4) Z1(5)=(34,32)T,Z2(5)=(213,6)T,Z1(5)=Z1(4),Z2(5)=Z2(4),
故聚类结束,两聚类中心为 m 1 = ( 4 3 , 2 3 ) T , m 2 = ( 13 2 , 6 ) T , ω 1 : x 1 , x 2 , x 3 ; ω 2 : x 4 , x 5 m_1=(\frac{4}{3},\frac{2}{3})^T,m_2=(\frac{13}{2},6)^T,\omega_1:x_1,x_2,x_3;\omega_2:x_4,x_5 m1=(34,32)T,m2=(213,6)T,ω1:x1,x2,x3;ω2:x4,x5。
(9)若有下列两类样本:
| 训练样本号k | 1 2 3 4 | 1 2 3 4 |
|---|---|---|
| 特征 x 1 x_1 x1 | 0 1 1 1 | 0 0 0 1 |
| 特征 x 2 x_2 x2 | 0 0 0 1 | 0 1 1 1 |
| 特征 x 3 x_3 x3 | 0 0 1 0 | 1 0 1 1 |
| 类别 | ω 1 \omega_1 ω1 | ω 2 \omega_2 ω2 |
-
试用 K − L K-L K−L 变换,将其降到 1 1 1 维特征空间;
-
求其最佳鉴别 F i s h e r Fisher Fisher 矢量 W = S ω − 1 ( m 1 − m 2 ) W={S_\omega}^{-1}(m_1-m_2) W=Sω−1(m1−m2) 及 F i s h e r Fisher Fisher 判别函数。
解:
1)
E ( X X T ) = 1 8 [ ( 0 1 1 1 0 0 0 1 0 0 1 0 ) ( 0 0 0 1 0 0 1 0 1 1 1 0 ) + ( 0 0 0 1 0 1 1 1 1 0 1 1 ) ( 0 0 1 0 1 0 0 1 1 1 1 1 ) ] = ( 1 2 1 4 1 4 1 4 1 2 1 4 1 4 1 4 1 2 ) \begin{aligned}E(XX^T)&=\frac{1}{8}[\left(\begin{matrix}0&1&1&1\\0&0&0&1\\0&0&1&0\end{matrix}\right)\left(\begin{matrix}0&0&0\\1&0&0\\1&0&1\\1&1&0\end{matrix}\right)+\left(\begin{matrix}0&0&0&1\\0&1&1&1\\1&0&1&1\end{matrix}\right)\left(\begin{matrix}0&0&1\\0&1&0\\0&1&1\\1&1&1\end{matrix}\right)]\\&=\left(\begin{matrix}\frac{1}{2}&\frac{1}{4}&\frac{1}{4}\\\frac{1}{4}&\frac{1}{2}&\frac{1}{4}\\\frac{1}{4}&\frac{1}{4}&\frac{1}{2}\end{matrix}\right)\end{aligned} E(XXT)=81[⎝⎛000100101110⎠⎞⎝⎜⎜⎛011100010010⎠⎟⎟⎞+⎝⎛001010011111⎠⎞⎝⎜⎜⎛000101111011⎠⎟⎟⎞]=⎝⎛214141412141414121⎠⎞
λ = ( 1 4 0 0 0 1 4 0 0 0 1 ) , μ = ( 0 − 2 6 1 3 1 2 1 6 1 3 − 1 2 1 6 1 3 ) \lambda=\left(\begin{matrix}\frac{1}{4}&0&0\\0&\frac{1}{4}&0\\0&0&1\end{matrix}\right),\mu=\left(\begin{matrix}0&-\frac{2}{\sqrt6}&\frac{1}{\sqrt3}\\\frac{1}{\sqrt2}&\frac{1}{\sqrt6}&\frac{1}{\sqrt3}\\-\frac{1}{\sqrt2}&\frac{1}{\sqrt6}&\frac{1}{\sqrt3}\end{matrix}\right) λ=⎝⎛41000410001⎠⎞,μ=⎝⎜⎛021−21−626161313131⎠⎟⎞,
用最大特征根 λ = 1 \lambda=1 λ=1 的特征向量 μ 1 = 1 3 ( 1 , 1 , 1 ) T \mu_1=\frac{1}{\sqrt{3}}(1,1,1)^T μ1=31(1,1,1)T 将样本降到一维空间,
ω 1 : 0 1 3 2 3 2 3 \omega_1:0 \frac{1}{\sqrt3} \frac{2}{\sqrt3} \frac{2}{\sqrt3} ω1:0 31 32 32,
ω 2 : 1 3 1 3 2 3 3 3 \omega_2:\frac{1}{\sqrt3} \frac{1}{\sqrt3} \frac{2}{\sqrt3} \frac{3}{\sqrt3} ω2:31 31 32 33。
2) W = S ω − 1 ( m 1 − m 2 ) = ( 6 , − 6 , − 6 ) T W={S_\omega}^{-1}(m_1-m_2)=(6,-6,-6)^T W=Sω−1(m1−m2)=(6,−6,−6)T,
ω 1 : 0 , 6 , 0 , 0 ; ω 2 : − 6 , − 6 , − 12 , − 6 \omega_1:0,6,0,0;\omega_2:-6,-6,-12,-6 ω1:0,6,0,0;ω2:−6,−6,−12,−6,
y t = Y 1 ‾ + Y 2 ‾ 2 = W T X 1 ‾ + W T X 2 ‾ 2 = − 3 y_t=\frac{\overline{Y_1}+{\overline{Y_2}}}{2}=\frac{W^T\overline{X_1}+W^T\overline{X_2}}{2}=-3 yt=2Y1+Y2=2WTX1+WTX2=−3,
Y = W T X ⟹ 6 x 1 − 6 x 2 − 6 x 3 = − 3 ⟹ 2 x 1 − 2 x 2 − 2 x 3 = − 1 Y=W^TX\Longrightarrow 6x_1-6x_2-6x_3=-3\Longrightarrow 2x_1-2x_2-2x_3=-1 Y=WTX⟹6x1−6x2−6x3=−3⟹2x1−2x2−2x3=−1,
当 Y = W T X = 2 x 1 − 2 x 2 − 2 x 3 > − 1 Y=W^TX=2x_1-2x_2-2x_3>-1 Y=WTX=2x1−2x2−2x3>−1 时, X ∈ ω 1 X\in \omega_1 X∈ω1,
当 Y = W T X = 2 x 1 − 2 x 2 − 2 x 3 < − 1 Y=W^TX=2x_1-2x_2-2x_3<-1 Y=WTX=2x1−2x2−2x3<−1 时, X ∈ ω 2 X\in \omega_2 X∈ω2。
(10)如标准数字
1
1
1 在
7
∗
5
7*5
7∗5 的方格中表示成如图所示的黑白图像,黑为
1
1
1,白为
0
0
0,现若有一数字
1
1
1 在
7
∗
5
7*5
7∗5 网格中向左错了一列。试用分别计算要与标准模板之间的欧氏距离、绝对值偏差、偏差的夹角表示,以及用“异或”计算两者差异。

解: X = ( 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 ) , X 1 = ( 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 ) X=\left(\begin{matrix}0&0&1&0&0\\0&0&1&0&0\\0&0&1&0&0\\0&0&1&0&0\\0&0&1&0&0\\0&0&1&0&0\\0&0&1&0&0\end{matrix}\right),X^1=\left(\begin{matrix}0&1&0&0&0\\0&1&0&0&0\\0&1&0&0&0\\0&1&0&0&0\\0&1&0&0&0\\0&1&0&0&0\\0&1&0&0&0\end{matrix}\right) X=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛00000000000000111111100000000000000⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞,X1=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛00000001111111000000000000000000000⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞。
∣ ∣ X − X 1 ∣ ∣ = 14 ||X-X^1||=\sqrt{14} ∣∣X−X1∣∣=14(欧氏距离)
∣ X − X 1 ∣ = 14 |X-X^1|=14 ∣X−X1∣=14(绝对值偏差)
S ( X , X 1 ) = X T X 1 ∣ ∣ X T ∣ ∣ ∣ ∣ X 1 ∣ ∣ = 0 ⟹ θ = 90 ∘ S(X,X^1)=\frac{X^TX^1}{||X^T||||X^1||}=0\Longrightarrow \theta={90}^{\circ} S(X,X1)=∣∣XT∣∣∣∣X1∣∣XTX1=0⟹θ=90∘。
(11)设两类样本的类内离散矩阵分别为 S 1 = [ 1 1 2 1 2 1 ] S_1=\left[\begin{matrix}1&\frac{1}{2}\\\frac{1}{2}&1\end{matrix}\right] S1=[121211], S 2 = [ 1 − 1 2 − 1 2 1 ] S_2=\left[\begin{matrix}1&-\frac{1}{2}\\-\frac{1}{2}&1\end{matrix}\right] S2=[1−21−211], m 1 = ( 2 , 0 ) T , m 2 = ( 2 , 2 ) T m_1=(2,0)^T,m_2=(2,2)^T m1=(2,0)T,m2=(2,2)T,试用 f i s h e r fisher fisher 准则求其决策面方程。
解:
总类内离散度矩阵: S ω = 1 2 ( S 1 + S 2 ) = ( 1 0 0 1 ) S_\omega=\frac{1}{2}(S_1+S_2)=\left(\begin{matrix}1&0\\0&1\end{matrix}\right) Sω=21(S1+S2)=(1001),
F i s h e r Fisher Fisher 最佳投影方向: W ∗ = S ω − 1 ( m 1 − m 2 ) = ( 0 − 2 ) T W^*={S_\omega}^{-1}(m_1-m_2)=(0 -2)^T W∗=Sω−1(m1−m2)=(0 −2)T,
两类样本分布形状相同(只是方向不同),因此 y 0 y_0 y0 应为两类均值投影的中点:
y 0 = W ∗ T m 1 + m 2 2 = ( 0 − 2 ) ( 2 1 ) = − 2 y_0={W^*}^T\frac{m_1+m_2}{2}=(0 -2)\left(\begin{matrix}2\\1\end{matrix}\right)=-2 y0=W∗T2m1+m2=(0 −2)(21)=−2,
决策面方程 d ( X ) = W ∗ T X + 2 d(X)={W^*}^TX+2 d(X)=W∗TX+2,
最佳线性分界面 W ∗ T ( x 1 , x 2 ) T = − 2 ⟹ − 2 x 2 = − 2 ⟹ x 2 = 1 {W^*}^T(x_1,x_2)^T=-2\Longrightarrow -2x_2=-2\Longrightarrow x_2=1 W∗T(x1,x2)T=−2⟹−2x2=−2⟹x2=1,
故 x 2 > 1 x_2>1 x2>1 时,属于第一类; x 2 < 1 x_2<1 x2<1 时,属于第二类。
(12)设一个二维空间中的两类样本服从正态分布,其参数分别为 μ 1 = ( 0 , 1 ) T , ∑ 1 = [ 1 0 0 1 ] , μ 2 = ( − 1 , 0 ) T , ∑ 2 = [ 2 0 0 2 ] \mu_1=(0,1)^T,\sum_1=\left[\begin{matrix}1&0\\0&1\end{matrix}\right],\mu_2=(-1,0)^T,\sum_2=\left[\begin{matrix}2&0\\0&2\end{matrix}\right] μ1=(0,1)T,∑1=[1001],μ2=(−1,0)T,∑2=[2002],先验概率 P ( ω 1 ) = P ( ω 2 ) P(\omega_1)=P(\omega_2) P(ω1)=P(ω2),试证明其基于最小错误率的贝叶斯决策分界面方程为一圆,并求其方程。
解:先验概率相等条件下,基于最小错误率贝叶斯决策的分界面上两类条件概率密度函数相等。因此:
− 1 2 ( X − μ 1 ) T ∑ 1 − 1 ( X − μ 1 ) − 1 2 ln ∣ ∑ 1 ∣ = − 1 2 ( X − μ 2 ) T ∑ 2 − 1 ( X − μ 2 ) − 1 2 ln ∣ ∑ 2 ∣ -\frac{1}{2}(X-{\mu}_1)^T{\sum_1}^{-1}(X-{\mu}_1)-\frac{1}{2}\ln|{\sum}_1|=-\frac{1}{2}(X-{\mu}_2)^T{\sum_2}^{-1}(X-{\mu}_2)-\frac{1}{2}\ln|{\sum}_2| −21(X−μ1)T∑1−1(X−μ1)−21ln∣∑1∣=−21(X−μ2)T∑2−1(X−μ2)−21ln∣∑2∣,
( x 1 x 2 − 1 ) ( 1 0 0 1 ) ( x 1 x 2 − 1 ) − ln 1 = ( x 1 + 1 x 2 ) ( 1 2 0 0 1 2 ) ( x 1 + 1 x 2 ) + ln 4 (x_1 x_2-1)\left(\begin{matrix}1&0\\0&1\end{matrix}\right)\left(\begin{matrix}x_1\\x_2-1\end{matrix}\right)-\ln1=(x_1+1 x_2)\left(\begin{matrix}\frac{1}{2}&0\\0&\frac{1}{2}\end{matrix}\right)\left(\begin{matrix}x_1+1\\x_2\end{matrix}\right)+\ln4 (x1 x2−1)(1001)(x1x2−1)−ln1=(x1+1 x2)(210021)(x1+1x2)+ln4,
x 1 2 + ( x 2 − 1 ) 2 = 1 2 ( x 1 + 1 ) 2 + 1 2 x 2 2 + ln 4 {x_1}^2+(x_2-1)^2=\frac{1}{2}(x_1+1)^2+\frac{1}{2}{x_2}^2+\ln4 x12+(x2−1)2=21(x1+1)2+21x22+ln4,
( x 1 − 1 ) 2 + ( x 2 − 2 ) 2 = 4 + 2 ln 4 (x_1-1)^2+(x_2-2)^2=4+2\ln4 (x1−1)2+(x2−2)2=4+2ln4,为一圆方程。
四、填空题
1、蚁群算法解
T
S
P
TSP
TSP 问题时,蚂蚁从城市
i
i
i 到城市
j
j
j 的转移概率的计算公式是:
p
i
j
k
(
t
)
=
[
τ
i
j
(
t
)
]
α
⋅
[
η
i
j
]
β
∑
l
∈
J
i
k
[
τ
i
j
(
t
)
]
α
⋅
[
η
i
j
]
β
{p_{ij}}^k(t)=\frac{[\tau_{ij}(t)]^{\alpha}\cdot[\eta_{ij}]^{\beta}}{\sum\limits_{l\in {J_i}^k}[\tau_{ij}(t)]^{\alpha}\cdot[\eta_{ij}]^{\beta}}
pijk(t)=l∈Jik∑[τij(t)]α⋅[ηij]β[τij(t)]α⋅[ηij]β
2、
P
S
O
PSO
PSO 算法中,个体速度增量、速度更新和个体位置更新的三个计算公式是:
Δ
v
i
k
=
c
1
⋅
r
a
n
d
(
)
⋅
(
p
b
e
s
t
i
k
−
s
i
k
)
+
c
2
⋅
r
a
n
d
(
)
⋅
(
g
b
e
s
t
k
−
s
i
k
)
v
i
k
+
1
=
v
i
k
+
Δ
v
i
k
s
i
k
+
1
=
s
i
k
+
v
i
k
+
1
\begin{aligned} \Delta{v_i}^k&=c_1\cdot rand()\cdot({pbest_i}^k-{s_i}^k)+c_2\cdot rand()\cdot(gbest^k-{s_i}^k)\\ {v_i}^{k+1}&={v_i}^k+\Delta{v_i}^k\\ {s_i}^{k+1}&={s_i}^k+{v_i}^{k+1} \end{aligned}
Δvikvik+1sik+1=c1⋅rand()⋅(pbestik−sik)+c2⋅rand()⋅(gbestk−sik)=vik+Δvik=sik+vik+1
3、
A
S
O
ASO
ASO 算法中,第
k
k
k 只蚂蚁从
t
t
t 时刻到
t
+
1
t+1
t+1 时刻,在从态
i
i
i 到
j
j
j 时,所采用的信息素增量、更新和转移概率所涉及的三个计算公式是:
Δ
τ
i
j
(
t
)
=
∑
k
=
1
m
Δ
τ
i
j
k
(
t
)
τ
i
j
(
t
)
=
(
1
−
ρ
)
τ
i
j
(
t
)
+
Δ
τ
i
j
(
t
)
p
i
j
k
(
t
)
=
[
τ
i
j
(
t
)
]
α
⋅
[
η
i
j
]
β
∑
l
∈
J
i
k
[
τ
i
j
(
t
)
]
α
⋅
[
η
i
j
]
β
\begin{aligned} \Delta\tau_{ij}(t)&=\sum\limits_{k=1}^{m}\Delta{\tau_{ij}}^k(t)\\ \tau_{ij}(t)&=(1-\rho)\tau_{ij}(t)+\Delta\tau_{ij}(t)\\ {p_{ij}}^k(t)&=\frac{[\tau_{ij}(t)]^{\alpha}\cdot[\eta_{ij}]^{\beta}}{\sum\limits_{l\in {J_i}^k}[\tau_{ij}(t)]^{\alpha}\cdot[\eta_{ij}]^{\beta}} \end{aligned}
Δτij(t)τij(t)pijk(t)=k=1∑mΔτijk(t)=(1−ρ)τij(t)+Δτij(t)=l∈Jik∑[τij(t)]α⋅[ηij]β[τij(t)]α⋅[ηij]β
4、模糊
k
k
k 均值聚类,每个样本到子类的模糊隶属度矩阵
U
=
(
u
i
j
)
(
i
=
1
,
2
,
⋅
⋅
⋅
,
k
;
j
=
1
,
2
,
⋅
⋅
⋅
,
N
)
(
k
U=(u_{ij})(i=1,2,···,k;j=1,2,···,N)(k
U=(uij)(i=1,2,⋅⋅⋅,k;j=1,2,⋅⋅⋅,N)(k 为类数,
N
N
N 为样本数
)
)
)中的
u
i
j
u_{ij}
uij 的更新公式是:
u
i
j
(
L
+
1
)
=
1
∑
p
=
1
K
(
d
i
j
d
p
j
)
2
m
−
1
u_{ij}(L+1)=\frac{1}{\sum\limits_{p=1}^{K}(\frac{d_{ij}}{d_{pj}})^{\frac{2}{m-1}}}
uij(L+1)=p=1∑K(dpjdij)m−121
5、阈值 b b b 和偏置 θ \theta θ 的关系是: b = − θ b=-\theta b=−θ。
6、文法 G G G 的四元组表达式为: G = ( V T , V N , S , P ) G=(V_T,V_N,S,P) G=(VT,VN,S,P);四种文法的包含关系为:3型 ⊆ \subseteq ⊆ 2型 ⊆ \subseteq ⊆ 1型 ⊆ \subseteq ⊆ 0型。
7、信息系统的四元组表达形式为:
S
=
<
U
,
A
,
V
,
f
>
S=<U,A,V,f>
S=<U,A,V,f>。论域
U
U
U 的子集
X
X
X 在
U
U
U 上的等价关系
R
R
R 下的上近似集、下近似集和边界域表示公式分别为:
上
:
R
‾
(
X
)
=
{
x
∣
x
∈
U
,
[
x
]
R
∩
X
≠
∅
}
下
:
R
‾
(
X
)
=
{
x
∣
x
∈
U
,
[
x
]
R
⊆
X
}
边
:
B
N
D
R
(
X
)
=
R
‾
(
X
)
−
R
‾
(
X
)
\begin{aligned} 上:&\overline{R}(X)=\{x\mid x\in U,[x]_R\cap X\ne \varnothing \}\\ 下:&\underline{R}(X)=\{x\mid x\in U,[x]_R\subseteq X\}\\ 边:&BND_R(X)=\overline{R}(X)-\underline{R}(X)\\ \end{aligned}
上:下:边:R(X)={x∣x∈U,[x]R∩X=∅}R(X)={x∣x∈U,[x]R⊆X}BNDR(X)=R(X)−R(X)
五、计算题
(1)在 P S O PSO PSO 解 T S P TSP TSP 问题时,由于可行解必须是一个置换,所以,速度以及个体向个体最优和全局最优的运动必须改用相应的变换来完成,因而产生了变换子和变换序的概念。
1. 设 5 5 5 城市的一个可行解 S = ( 1 , 2 , 3 , 4 , 5 ) S=(1,2,3,4,5) S=(1,2,3,4,5),变换子 S O = ( i 1 , i 2 ) = ( 2 , 4 ) SO=(i_1,i_2)=(2,4) SO=(i1,i2)=(2,4),计算 S ’ = S ◙ S O S’=S◙SO S’=S◙SO。
解:
S
’
=
S
◙
S
O
=
S
◙
(
2
,
4
)
=
(
1
,
4
,
3
,
2
,
5
)
S’=S◙SO= S◙(2,4) =(1,4,3,2,5)
S’=S◙SO=S◙(2,4)=(1,4,3,2,5)
2. 设
S
=
(
1
,
2
,
3
,
4
,
5
)
S=(1,2,3,4,5)
S=(1,2,3,4,5),变换序
S
S
=
(
2
,
4
)
,
(
3
,
5
)
,
(
1
,
3
)
SS={ (2,4),(3,5),(1,3)}
SS=(2,4),(3,5),(1,3), 计算
S
’
=
S
◙
S
S
S’=S ◙ SS
S’=S◙SS。
解:
S
’
=
S
◙
S
O
=
(
1
,
4
,
3
,
2
,
5
)
◙
{
(
3
,
5
)
,
(
1
,
3
)
}
=
(
1
,
4
,
5
,
2
,
3
)
◙
(
1
,
3
)
=
(
5
,
4
,
1
,
2
,
3
)
\begin{aligned} S’=S◙SO&=(1,4,3,2,5)◙\{(3,5),(1,3)\}\\ &=(1,4,5,2,3)◙(1,3)\\ &=(5,4,1,2,3) \end{aligned}
S’=S◙SO=(1,4,3,2,5)◙{(3,5),(1,3)}=(1,4,5,2,3)◙(1,3)=(5,4,1,2,3)
3. 设
A
=
(
1
,
2
,
3
,
4
,
5
)
,
B
=
(
5
,
3
,
2
,
1
,
4
)
A=(1,2,3,4,5),B=(5,3,2,1,4)
A=(1,2,3,4,5),B=(5,3,2,1,4),求
S
S
SS
SS,使得
A
=
B
◙
S
S
A=B ◙ SS
A=B◙SS。
解:
①先比较
A
A
A 和
B
B
B,不同值的位有
1
,
2
,
3
,
4
,
5
1,2,3,4,5
1,2,3,4,5。因
A
A
A 中的
A
(
1
)
=
B
(
4
)
A(1)=B(4)
A(1)=B(4),所以
S
O
1
=
{
(
1
,
4
)
}
,
S
S
=
S
S
∪
S
O
1
=
{
(
1
,
4
)
}
,
B
1
=
B
◙
S
O
1
=
(
1
,
3
,
2
,
5
,
4
)
{SO}_1=\{(1,4)\},SS=SS \cup {SO}_1=\{(1,4)\},B_1=B◙{SO}_1=(1,3,2,5,4)
SO1={(1,4)},SS=SS∪SO1={(1,4)},B1=B◙SO1=(1,3,2,5,4)。
②再比较
A
A
A 和
B
1
B_1
B1,不同值的位有
2
,
3
,
4
,
5
2,3,4,5
2,3,4,5。因
A
A
A 中的
A
(
2
)
=
B
1
(
3
)
A(2)=B_1(3)
A(2)=B1(3),所以
S
O
2
=
{
(
2
,
3
)
}
,
S
S
=
S
S
∪
S
O
2
=
{
(
1
,
4
)
,
(
2
,
3
)
}
,
B
2
=
B
1
◙
S
O
2
=
(
1
,
2
,
3
,
5
,
4
)
{SO}_2=\{(2,3)\},SS=SS\cup {SO}_2=\{(1,4),(2,3)\},B_2=B_1◙{SO}_2=(1,2,3,5,4)
SO2={(2,3)},SS=SS∪SO2={(1,4),(2,3)},B2=B1◙SO2=(1,2,3,5,4)。
③再比较
A
A
A 和
B
2
B_2
B2,不同值的位有
4
,
5
4,5
4,5。因
A
A
A 中的
A
(
4
)
=
B
2
(
5
)
A(4)=B_2(5)
A(4)=B2(5),所以
S
O
3
=
{
(
4
,
5
)
}
,
S
S
=
S
S
∪
S
O
3
=
{
(
1
,
4
)
,
(
2
,
3
)
,
(
4
,
5
)
}
,
B
3
=
B
2
◙
S
O
3
=
(
1
,
2
,
3
,
4
,
5
)
{SO}_3=\{(4,5)\},SS=SS\cup {SO}_3=\{(1,4),(2,3),(4,5)\},B_3=B_2◙{SO}_3=(1,2,3,4,5)
SO3={(4,5)},SS=SS∪SO3={(1,4),(2,3),(4,5)},B3=B2◙SO3=(1,2,3,4,5)。
④再比较
A
A
A 和
B
3
B_3
B3。相同,停止。得解:
S
S
=
{
(
1
,
4
)
,
(
2
,
3
)
,
(
4
,
5
)
}
SS=\{(1,4),(2,3),(4,5)\}
SS={(1,4),(2,3),(4,5)},一定有:
A
=
B
◙
S
S
A=B◙SS
A=B◙SS。
(2)在
P
S
O
PSO
PSO 方法解类数固定为
M
M
M 的聚类问题时,设计粒子、速度、个体历史最优解、全局最优解的
M
A
T
L
A
B
MATLAB
MATLAB 语言描述形式以及个体适应度的计算方式和惯性权重随迭代步减小的公式。
解:
S
a
m
p
l
e
s
X
=
{
X
i
∣
i
=
1
,
2
,
…
,
N
}
,
X
i
—
n
−
d
i
m
e
n
s
i
o
n
a
l
v
e
c
t
o
r
P
a
r
t
i
t
i
o
n
C
=
C
1
,
C
2
,
⋅
⋅
⋅
,
C
M
J
=
∑
j
=
1
M
∑
X
∈
C
j
d
(
X
,
m
j
)
,
m
j
=
1
∣
C
j
∣
∑
X
∈
C
j
X
d
(
X
,
m
j
)
=
min
k
=
1
,
2
,
⋅
⋅
⋅
,
M
d
(
X
,
m
k
)
⟹
X
∈
C
i
Samples X=\{X_i|i=1,2,…,N\},\\ Xi—n-dimensional vector\\ Partition C={C_1, C_2,···, C_M}\\ J=\sum\limits_{j=1}^{M}\sum\limits_{X\in C_j}d(X,m_j),m_j=\frac{1}{|C_j|}\sum\limits_{X\in C_j}X\\ d(X,m_j)=\min_{k=1,2,···,M}d(X,m_k)\Longrightarrow X\in C_i\\
SamplesX={Xi∣i=1,2,…,N},Xi—n−dimensionalvectorPartitionC=C1,C2,⋅⋅⋅,CMJ=j=1∑MX∈Cj∑d(X,mj),mj=∣Cj∣1X∈Cj∑Xd(X,mj)=k=1,2,⋅⋅⋅,Mmind(X,mk)⟹X∈Ci
Particle(i)={
location[ ],
velocity[ ],
fitness
}
Particle(i).location[ ]={m1,m2,…,mM}
Particle(i).velocity[ ]={V1,V2,…,VM}
Particle(i).fitness=k/J
Pid(i)={ location[ ],
velocity[ ],
fitness
}
Pgd={ location[ ],
velocity[ ],
fitness
}
Particle(i).velocity[ ]=wParticle(i).velocity[]
+η1rand(){Pid(i). location[ ]-Particle (i). location[ ])
+η2rand(){Pgd. location[ ]-Particle (i). location[ ])
Particle(i).location[ ] = Particle(i).location[ ]+ Particle(i).velocity[ ]
P a r a m e t e r s : η 1 = η 2 = 2 Parameters: η_1= η_2 =2 Parameters:η1=η2=2,
w
=
w
m
a
x
−
i
t
e
r
w
m
a
x
−
w
m
i
n
i
t
e
r
m
a
x
,
w
m
a
x
=
1
,
w
m
i
n
=
0
,
i
t
e
r
m
a
x
:
m
a
x
a
l
t
i
m
e
s
w=w_{max}-iter\frac{w_{max}-w_{min}}{itermax},w_{max}=1,w_{min}=0,itermax:maxal times
w=wmax−iteritermaxwmax−wmin,wmax=1,wmin=0,itermax:maxal times。
(3)设抗原编码对应的向量表示为
X
=
(
1
,
1
,
0
,
1
,
1
)
T
X=(1,1,0,1,1)^T
X=(1,1,0,1,1)T,抗体编码对应的向量表示为
Y
=
(
1
,
0
,
0
,
1
,
0
)
T
Y=(1,0,0,1,0)^T
Y=(1,0,0,1,0)T,计算它们的亲和度。
解:1. 用汉明距离:
H
(
X
,
Y
)
=
1
2
(
m
−
X
T
Y
)
=
1.5
亲
和
度
f
=
1
1
+
H
(
X
,
Y
)
=
0.4
H(X,Y)=\frac{1}{2}(m-X^TY)=1.5\\ 亲和度f=\frac{1}{1+H(X,Y)}=0.4
H(X,Y)=21(m−XTY)=1.5亲和度f=1+H(X,Y)1=0.4
或者用异或计算:
H
(
X
,
Y
)
=
2
亲
和
度
f
=
1
1
+
H
(
X
,
Y
)
≈
0.33
H(X,Y)=2\\ 亲和度f=\frac{1}{1+H(X,Y)}\approx0.33
H(X,Y)=2亲和度f=1+H(X,Y)1≈0.33
2.用欧氏距离:
D
(
X
,
Y
)
=
2
=
1.414
亲
和
度
f
=
1
1
+
D
(
X
,
Y
)
≈
0.41
D(X,Y)=\sqrt{2}=1.414\\ 亲和度f=\frac{1}{1+D(X,Y)}\approx0.41
D(X,Y)=2=1.414亲和度f=1+D(X,Y)1≈0.41
3.用城市距离:
M
(
X
,
Y
)
=
2
亲
和
度
f
=
1
1
+
M
(
X
,
Y
)
≈
0.33
M(X,Y)=2\\ 亲和度f=\frac{1}{1+M(X,Y)}\approx0.33
M(X,Y)=2亲和度f=1+M(X,Y)1≈0.33
更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容








所有评论(0)