---

前言

这是大三学习模式识别的笔记第一弹，有错误欢迎指出，不胜感激

---

一、决策面与判别函数

什么是决策面？
在特征空间中，将不同种类样本分开的决策边界称为决策面。举个例子，在二维平面，一条直线即可成为一个决策面，它所划分的两个区域即成为两个特征子空间。

什么是判别函数？
用数学形式表示的决策面即为判别函数。上面的例子中，y=ax+b即可成为判别函数，但往往写成ax+by+c=0，ax+by+c>0是一类，ax+by+c<0是另一类。类似的可以推广。

二、分类器——线性分类器

1.特点

线性分类器：对于两类的分类问题，采用线性判别函数划分特征空间（即采用直线或平面等将两类样本在特征空间中的区域划分开），这样的分类器是线性分类器。

线性分类器特点：特征空间一分为二，适合于解决两类的分类问题，即二分类问题。

线性分类器能不能解决多分类问题呢？答案是肯定的。多分类问题可以分为多个二分类问题，至于怎样分成多个二分类问题，在机器学习中介绍了最简单的两种方式：OvO与OvR,此处不做详细介绍。

2.线性判别函数

我们往往用向量的形式表示判别函数，于是判别函数表示为

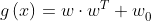
其中w为权向量，w0为阈值。

3.增广变换

对原特征向量X做增广变换（记作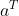)，权向量也做增广变换（记作y）如下所示


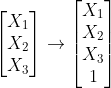
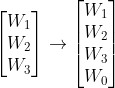
则判别函数表示为

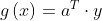
増广变换的特点：
特征维数增加了一维
样本向量实际还是位于原D维子空间中
样本之间的欧氏距离保持不变
增广变换后的决策面是过原点的超平面

4.线性分类器设计步骤

1.给定类别已知的样本集——训练集
2.选择一个准则函数J，其值反应分类器优劣
3.采用最优解的方法求准则函数J的极值解，从而获得权向量和阈值权

5.实例——垂直平分分类器与Fisher投影准则

1.垂直平分分类器
垂直平分分类器设计思路：基于两类样本均值点作垂直平分线。
垂直平分分类器等价的最小距离决策规则为：
对于未知样本x，若d1(x) <d2(x) ，则x决策为ω1类 若d1(x) >d2(x) ，则x决策为ω2类。

故而垂直平分分类器又叫最小距离分类器。

步骤：
1） 先求均值向量m1和m2
2）利用垂直几何关系，设权向量

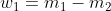
则直线方程为

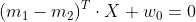
3)再利用平分几何关系，中点x0在直线上

解得阈值向量

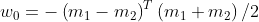
对于未知样本x，若g(x) > 0，则x决策为ω1类 若g(x) < 0，则x决策为ω2类

垂直平分分类器（最小距离分类器）的主要特点：
解决二分类问题的线性分类器
原则上对样本集无特殊要求
未采用准则函数求极值解（非最佳决策）
算法最简单，分类器设计最容易

2.Fisher准则
设计思路：通过投影对高维分类问题降维，Fisher将高维特征空间的样本投影到一维直线

Fisher投影准则的物理含义：
投影后异类样本尽量远离，投影后同类样本尽量靠近

在原特征空间中

在投影后的一维空间中


化简后为

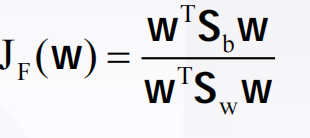
采用Lagrange乘子法求Fisher准则函数的极值（具体做法等我啥时候学会了再说吧）

Fisher投影的特点
解决两类问题的线性投影
原则上对样本集无特殊要求（Sw矩阵可逆）
采用Fisher投影准则函数求极值解（最佳决策
分类器设计较容易

---

总结

简要的总结了一下线性分类器