反向传播算法(过程及公式推导)_深度学习之反向传播算法(BP)
前向传播结构图在推导反向传播之前,首先我们需要了解深度神经网络的模型图,我简单的画个模型图:这是模型的最后两层,L代表输出层,假设有两个输出,,拼成一个输出列向量L-1层有三个节点,有三个输出,,,拼成一个输出列向量,这个输出也相当于是对第L层的输入,第L-1层和第L层满足如下矩阵关系:如果把权重向量拼成一个矩阵,的第i行的权重乘以上一层的输出然后传给...
·
前向传播结构图
在推导反向传播之前,首先我们需要了解深度神经网络的模型图,我简单的画个模型图:
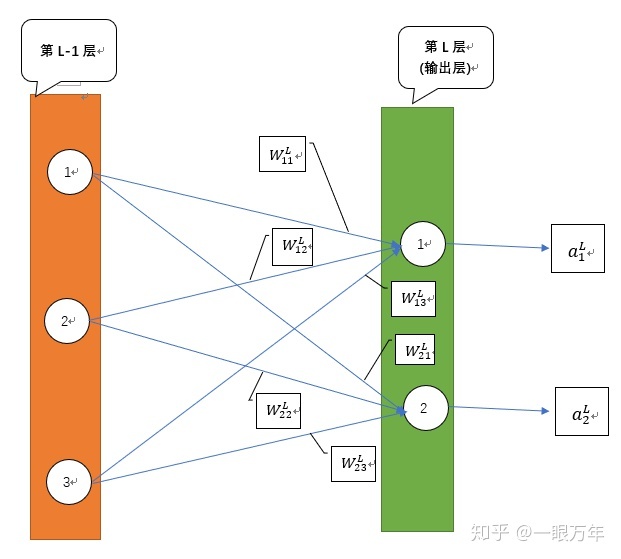
这是模型的最后两层,L代表输出层,假设有两个输出
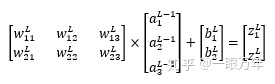
如果把权重向量拼成一个矩阵
定义一个损失函数
当输入通过一层层的神经网络前向传播到输出层,也就是第L层,得到
=
用前篇笔记所讲的标量对矩阵链式求导公式来推导BP算法
公式为: z =
链式关系:
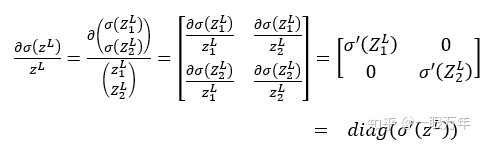
同理可求得
综上述可求出
我们知道了损失函数对L层参数的梯度,可以用梯度下降更新L层的参数
更一般的情况是假设第
进一步可得损失函数对
反向传播总结
基于随机梯度下降的反向传播算法
输入:训练集
1、随机初始化
repeat
对训练集
2、for n=1,2,3......N
从训练集取出样本
(2.1)、 for
进行前向传播计算,计算每一层的未激活的输出
(2.2)、通过损失函数计算输出层的
for
计算误差项的反向传播
for
(2.3) 、更新第
end
until 神经网络模型在验证集
输出:
参考
- ^参考以下博客 https://www.cnblogs.com/pinard/p/6422831.html
点击阅读全文
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容
目录









所有评论(0)