机器人学导论一
机器人学导论空间描述和变换位置描述空间描述和变换位置描述用三个相互正交的带有箭头的单位矢量来表示一个坐标系{A}。用一个矢量来表示一个点PPP
空间描述和变换
位置姿态与坐标系
位置的描述
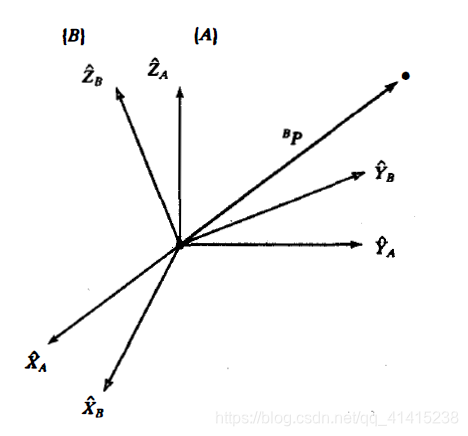
用三个相互正交的带有箭头的单位矢量来表示一个坐标系{A}。用一个矢量来表示一个点
A
P
^AP
AP
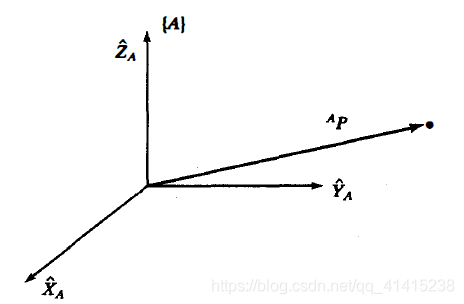
并且可等价地被认为是空间的一个位置,或者简单地用一组有序的三个数字来表示。矢量的各个元素用下标x, y和z来标明:
A
P
=
[
P
x
P
y
P
z
]
^AP= \begin{bmatrix} P_x \\ P_y \\P_z \end{bmatrix}
AP=⎣⎡PxPyPz⎦⎤
姿态的描述
为了描述物体的姿态,我们将在物体上固定一个坐标系并且给出此坐标系相对于参考系的表达。
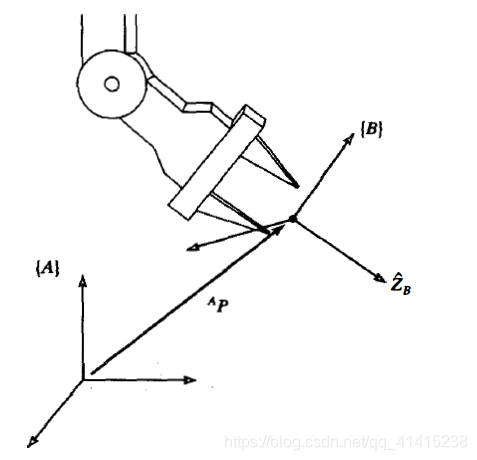
我们用
X
^
B
\hat{X}_B
X^B,
Y
^
B
\hat{Y}_B
Y^B,
Z
^
B
\hat{Z}_B
Z^B来表示坐标系{B}主轴方向的单位矢量。当用坐标系{A}的坐标表达时, 它们被写成
A
X
^
B
^A\hat{X}_B
AX^B,
A
Y
^
B
^A\hat{Y}_B
AY^B,
A
Z
^
B
^A\hat{Z}_B
AZ^B。我们很容易将这三个单位矢量按照
A
X
^
B
^A\hat{X}_B
AX^B,
A
Y
^
B
^A\hat{Y}_B
AY^B,
A
Z
^
B
^A\hat{Z}_B
AZ^B的顺序排列组成一个3x3的矩阵,我们称这个矩阵为旋转矩阵,井且由于这个特殊旋转矩阵是{B}相对千{A}的表达,所以我们用符号
B
A
R
{^A_B}R
BAR来表示:
B
A
R
=
[
A
X
^
B
A
Y
^
B
A
Z
^
B
]
=
[
r
11
r
12
r
13
r
21
r
22
r
23
r
31
r
32
r
33
]
{^A_B}R=\begin{bmatrix}^A\hat{X}_B&^A\hat{Y}_B&^A\hat{Z}_B\end{bmatrix}=\begin{bmatrix} r11&r12&r13 \\ r21&r22&r23 \\ r31&r32&r33 \end{bmatrix}
BAR=[AX^BAY^BAZ^B]=⎣⎡r11r21r31r12r22r32r13r23r33⎦⎤
标量
r
i
j
r_{ij}
rij可用每个矢量在其参考坐标系中单位方向上投影的分量来表示。于是,
B
A
R
{^A_B}R
BAR各个分量可用一对单位矢量的点积来表示:
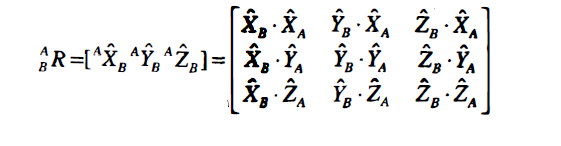
B
A
R
{^A_B}R
BAR为坐标系{A}相对于{B}的描述,那么{B}相对于{A}的转换可有
B
A
R
{^A_B}R
BAR的转置得到;即:
A
B
R
=
B
A
R
T
{^B_A}R={^A_B}R^T
ABR=BART
坐标系的描述
用 B A R {^A_B}R BAR和 A R B O R G {^A}R_{BORG} ARBORG来描述坐标系{B},其中 A R B O R G {^A}R_{BORG} ARBORG是确定坐标系{B}的原点的位置矢量: { B } = { B A R , A R B O R G } \lbrace B\rbrace=\lbrace {^A_B}R ,{^A}R_{BORG} \rbrace {B}={BAR,ARBORG}
关于平移旋转坐标系的映射
平移
A
P
=
B
P
+
A
R
B
O
R
G
^AP=^BP+{^A}R_{BORG}
AP=BP+ARBORG
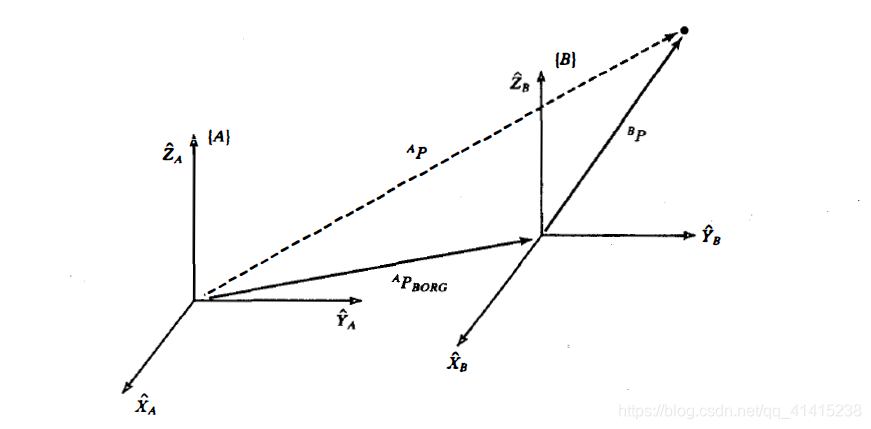
旋转
三个单位矢最排列在一起形成一个3 X 3的矩阵的列,我们称此矩阵为旋转矩阵。如果这个旋转矩阵专门是指{B}相对千{A}的描述,我们用符号
B
A
R
{^A_B}R
BAR来表示。
由于
B
A
R
{^A_B}R
BAR的列是{B}的单位矢量在{A}中的描述,所以
B
A
R
{^A_B}R
BAR的行是{A}的单位矢量在{B}中的描述。那么一个旋转矩阵即为三个一组的列向量或三个一组的行向量,即:
B
A
R
=
[
A
X
^
B
A
Y
^
B
A
Z
^
B
]
=
[
B
X
^
A
T
B
Y
^
A
T
B
Z
^
A
T
]
{^A_B}R=\begin{bmatrix}^A\hat{X}_B&^A\hat{Y}_B&^A\hat{Z}_B\end{bmatrix}=\begin{bmatrix}^B\hat{X}^T_A\\^B\hat{Y}^T_A\\^B\hat{Z}^T_A\end{bmatrix}
BAR=[AX^BAY^BAZ^B]=⎣⎡BX^ATBY^ATBZ^AT⎦⎤
我们已知矢量相对于某坐标系{B}的定义,现在想求矢量相对另一个坐标系{A}的定义,且这两个坐标系
的原点重合。
A
p
x
=
B
X
^
A
.
B
P
^Ap_x=^B\hat{X}_A.^BP
Apx=BX^A.BP
A
p
y
=
B
Y
^
A
.
B
P
^Ap_y=^B\hat{Y}_A.^BP
Apy=BY^A.BP
A
p
z
=
B
Z
^
A
.
B
P
^Ap_z=^B\hat{Z}_A.^BP
Apz=BZ^A.BP
可知{^A_B}R的行
B
X
^
A
^B\hat{X}_A
BX^A,
B
Y
^
A
^B\hat{Y}_A
BY^A,
B
Z
^
A
^B\hat{Z}_A
BZ^A,那 么可利用旋转矩阵将式简化成:
A
P
=
B
A
R
B
P
^AP={^A_B}R^BP
AP=BARBP
这个式子进行了一个映射一一它改变了矢量的描述一一将空间某点相对于{B}的描述
B
P
^BP
BP转换成了该点相对千{A}的描述
A
P
^AP
AP。
关于一般坐标系的映射
用一个矩阵形式的算子表示从一个坐标系到另一个坐标系的映射。 这比之外了的表达更简洁, 概念更明确。 定义一个4x4的矩阵算子并使用了4 X 1位置矢量, 式子就成为:
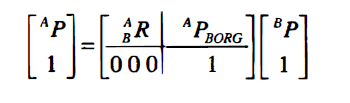
这个矩阵被称为齐次变换矩阵。它完全可以被看作是用一个简单的矩阵形式表示了一般变换的旋转和位移。
平移算子和旋转算子
平移算子
一个矢量相对千一个坐标系”向前移动”时,既可以认为是矢量”向前移动”,也可以认为坐标系”向后移动”,二者的数学表达式是相同的,只不过是观察位置不同。
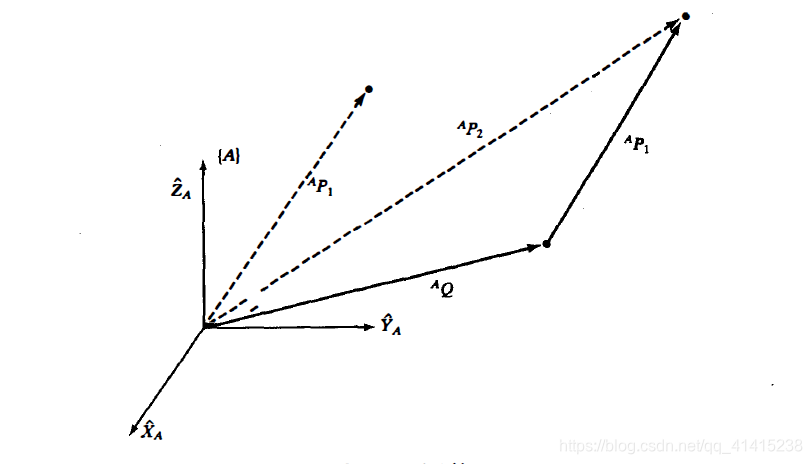
运算的结果是得到一个新的矢量
A
P
2
^AP_2
AP2
A
P
2
=
A
P
1
+
A
Q
^AP_2=^AP_1+^AQ
AP2=AP1+AQ用矩阵算子写出平移变换, 有:
A
P
2
=
D
Q
(
q
)
A
P
1
^AP_2=D_Q(q)^AP_1
AP2=DQ(q)AP1式中, q沿矢量Q方向平移的数量, 它是有符号的。算子
D
Q
D_Q
DQ可被看成是一个特殊形式的齐次变换:
D
Q
=
[
1
0
0
q
x
0
1
0
q
y
0
0
1
q
z
0
0
0
1
]
D_Q= \begin{bmatrix} 1 & 0&0&q_x \\ 0 & 1&0&q_y \\0 & 0&1&q_z\\0 & 0&0&1 \end{bmatrix}
DQ=⎣⎢⎢⎡100001000010qxqyqz1⎦⎥⎥⎤
旋转算子
将一个矢量
A
P
1
^AP_1
AP1用旋转R变换成一个新的矢最
A
P
2
^AP_2
AP2。
A
P
2
=
R
A
P
1
^AP_2=R^AP_1
AP2=RAP1

变换算子
将旋转算子和平移算子应用在一个坐标系上,能够的到一个齐次变换矩阵:经旋转R和平移Q的齐次变换矩阵与一个坐标系相对于参考坐标系经旋转R和平移Q的齐次 变换矩阵是相同的。
变换方程
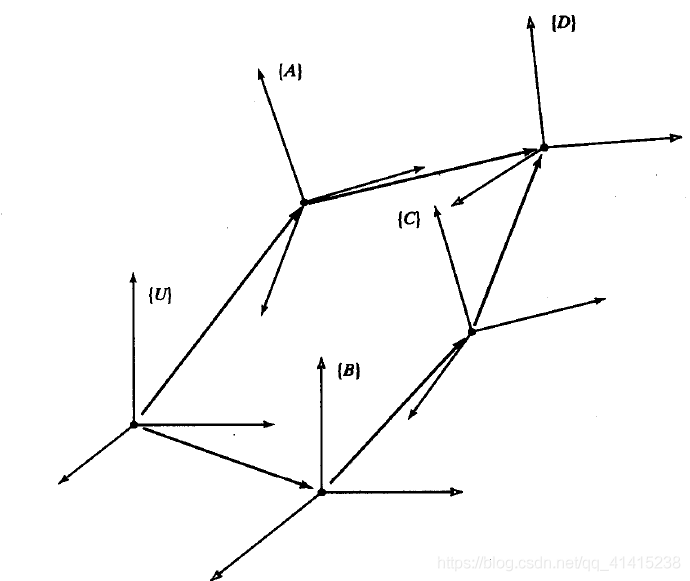
表示坐标系{D}可以用两种不同的方式表达成变换相乘的形式,第一种:
D
U
T
=
A
U
T
D
A
T
^U_DT=^U_AT^A_DT
DUT=AUTDAT第二种:
D
U
T
=
B
U
T
C
B
T
D
C
T
^U_DT=^U_BT^B_CT^C_DT
DUT=BUTCBTDCT将两个表达式构造成一个变换方程
A
U
T
D
A
T
=
B
U
T
C
B
T
D
C
T
^U_AT^A_DT=^U_BT^B_CT^C_DT
AUTDAT=BUTCBTDCT
如有n个未知变换和n个变换方程, 这个变换可由变换方程解出。如果除了
C
B
T
^B_CT
CBT外均已知,求
C
B
T
^B_CT
CBT:
C
B
T
=
B
U
T
−
1
D
A
T
D
C
T
−
1
^B_CT=^U_BT^{-1}{^A_D}T^C_DT^{-1}
CBT=BUT−1DATDCT−1
姿态的其他表述
首先将坐标系{B}和一个已知参考坐标系{A}重合。先将{B}绕
Z
^
B
\hat{Z}_B
Z^B旋转α角, 再绕
Y
^
B
\hat{Y}_B
Y^B旋转β角,最后绕
X
^
B
\hat{X}_B
X^B 旋转γ角。每次都是绕运动坐标系{B}的各轴旋转而不是绕固定坐标系{A}的各轴旋转。这样三个一组的旋转被称作欧拉角。注意每次旋转所绕的轴的方位取决于上次的旋转。由于三个旋转分别是绕着
Z
^
\hat{Z}
Z^,
Y
^
\hat{Y}
Y^,
X
^
\hat{X}
X^,所以称这种表示法为Z- Y-X欧拉角。
B
A
R
z
′
y
′
x
′
=
R
Z
(
α
)
R
Y
(
β
)
R
X
(
γ
)
=
[
c
α
−
s
α
0
s
α
c
α
0
0
0
1
]
[
c
β
0
s
β
0
1
0
−
s
β
0
c
β
]
[
1
0
0
0
c
γ
−
s
γ
0
s
γ
c
γ
]
^A_BR_{z'y'x'}=R_Z(α)R_Y(β)R_X(γ)=\begin{bmatrix} cα & -sα &0\\ sα & cα &0\\0 & 0 &1 \end{bmatrix}\begin{bmatrix} cβ &0 &sβ\\ 0 & 1&0\\-sβ & 0 &cβ \end{bmatrix}\begin{bmatrix} 1 &0 &0\\ 0 & cγ&-sγ\\0 & sγ &cγ \end{bmatrix}
BARz′y′x′=RZ(α)RY(β)RX(γ)=⎣⎡cαsα0−sαcα0001⎦⎤⎣⎡cβ0−sβ010sβ0cβ⎦⎤⎣⎡1000cγsγ0−sγcγ⎦⎤

B
A
R
z
′
y
′
x
′
(
α
,
β
,
γ
)
=
[
c
α
c
β
c
α
s
β
s
γ
−
s
α
c
γ
c
α
s
β
s
γ
+
s
α
c
γ
s
α
c
β
s
α
s
β
s
γ
+
c
α
c
γ
s
α
s
β
c
γ
−
c
α
s
γ
−
s
β
c
β
s
γ
c
β
c
γ
]
^A_BR_{z'y'x'}(α,β,γ)=\begin{bmatrix} cαcβ & cαsβsγ-sαcγ& cαsβsγ+sαcγ \\ sαcβ & sαsβsγ+cαcγ& sαsβcγ-cαsγ \\-sβ&cβsγ&cβcγ \end{bmatrix}
BARz′y′x′(α,β,γ)=⎣⎡cαcβsαcβ−sβcαsβsγ−sαcγsαsβsγ+cαcγcβsγcαsβsγ+sαcγsαsβcγ−cαsγcβcγ⎦⎤注意这个结果与以相反顺序绕固定轴旋转三次得到的结果完全相同!总之,这是一个不太直观的结果:三次绕固定轴旋转的最终姿态和以相反顺序三次绕运动坐标轴旋转的最终姿态相同。
欧拉角的变换一共有24种,绕固定坐标系旋转的有12种,绕变化后的坐标系旋转的有12种,方法都是一样的,算出绕每个轴的旋转矩阵,把后绕的矩阵右乘前绕的矩阵,就能得到整个旋转的矩阵。
John J.Craig《机器人学导论》(第四版)
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容








所有评论(0)