logit方程怎么写_简单易懂,结构方程模型思路总结
结构方程模型是结合了多种统计分析方法,可同时检验因子、分析项、误差项间的关系。本文将基于SPSSAU系统进行说明。1、方法辨别结构方程模型SEM包括测量关系和影响关系;既可以测量各因素内部结构及相关之间的关系情况,也可以测量多个自变量与多个因变量之间的影响关系。结构方程模型与路径分析主要区别就在于完整的结构方程模型包含了测量关系,如果仅包括影响关系,此时称作路径分析。如此以外,还有一些容易混淆的方

结构方程模型是结合了多种统计分析方法,可同时检验因子、分析项、误差项间的关系。本文将基于SPSSAU系统进行说明。
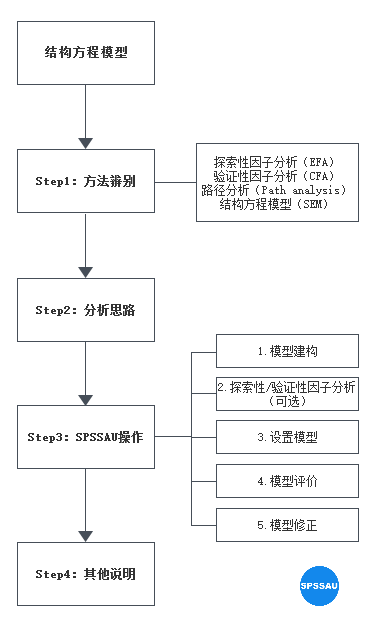
1、方法辨别
结构方程模型SEM包括测量关系和影响关系;既可以测量各因素内部结构及相关之间的关系情况,也可以测量多个自变量与多个因变量之间的影响关系。
结构方程模型与路径分析主要区别就在于完整的结构方程模型包含了测量关系,如果仅包括影响关系,此时称作路径分析。如此以外,还有一些容易混淆的方法,都在下表中列出:
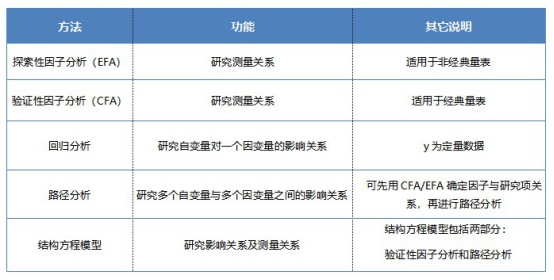
2、分析思路
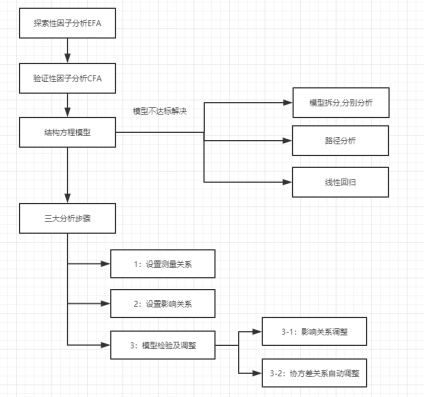
从整体分析角度看,完整分析可以包括以下几个步骤:模型构建→探索性因子分析/验证性因子分析→设置模型→评估模型→模型调整。
3、SPSSAU操作
下面通过案例进行说明。
案例:利用结构方程模型研究课程满意度
A1~A4:感知质量 B1~B3:感知价值 C1~C3:顾客满意 D1~D2:顾客忠诚

①理论模型构建
结构方程模型需要有完善的理论支持,分析前应结合自己的专业知识结合文献参考,建立初步的模型,同时可以先绘制出假设的模型或变量间关系,再通过分析验证这种观点或调整模型。
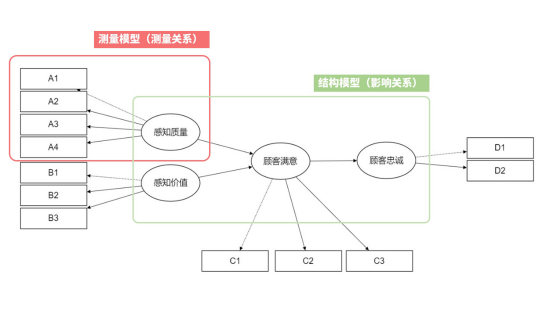
本例中,我们想要使用结构方程模型,构建顾客满意度模型。也就是研究感知质量(Factor1)和感知价值(Factor2)对于顾客满意度(Factor3)的影响关系,以及顾客满意度(Factor3)对顾客忠诚度(Factor4)的影响关系。
②前置步骤:探索性因子分析+验证性因子分析
结构方程模型对于数据质量,包括样本量,测量关系和影响关系均有着很高的要求,如果数据质量稍低则会导致拟合效果不佳,拟合指标不达标。
所以从分析角度看,在正式分析之前,需要保障测量关系具有良好的质量,通过探索性因子分析和验证性因子分析,共两步分析后,以保测量关系的高质量。
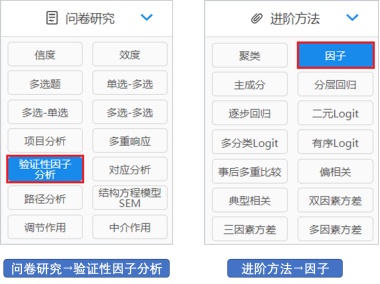
有关探索性因子分析与验证性因子分析的内容可查看SPSSAU帮助手册,里面有详细说明:
探索性因子分析
验证性因子分析
③设置模型
在确认好测量关系的高质量之后,接着正式进行结构方程模型构建。SPSSAU中可以直接使用结构方程模型。
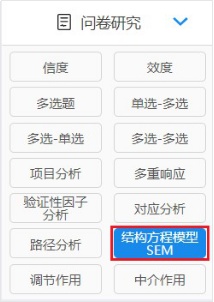
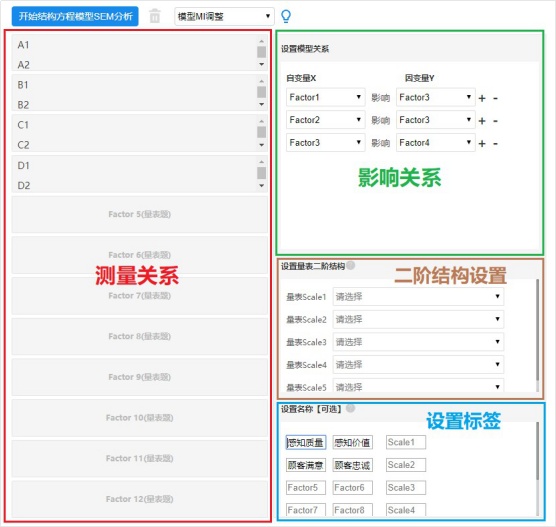
分别在SPSSAU平台上,设置好测量关系,影响关系后进行分析。
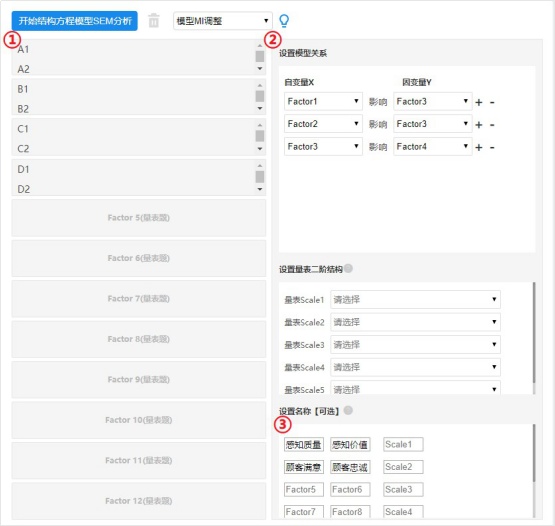
第一步:根据假设将对应分析项放入因子框,验证测量关系。
第二步:设置影响关系。
第三步:设置因子与量表标签,用于结构图展示。
- 二阶结构是在有一阶影响关系的基础上才需要设置,本例中暂不需要设置。
④模型评价
表1 模型回归系数表格
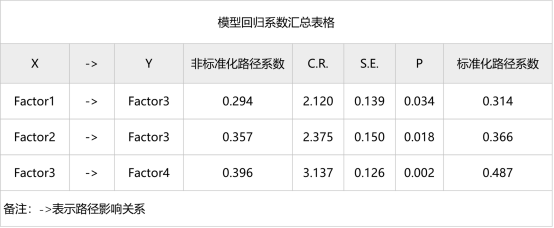
表1 提供了非标准化及标准化路径系数等指标,展示潜变量的影响关系,也就是看因子间的影响关系是否能成立。如果多个路径没呈现出显著性,可重新调整模型。
SPSAU提供了智能分析结果,可结合智能分析结果进行调整。

表2 载荷系数表格
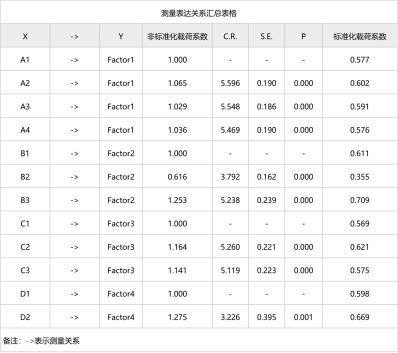
- C.R.值:为临界值,相当于t值,用于得到P值。
- S.E.值:估计值标准误,标准误越小,表明样本统计量与总体参数的值越接近。
表2展示的是测量关系情况。如果P值均呈现出显著性水平,标准化因子载荷系数大于0.5,则说明模型测量关系较好。如果出现某条路径没有呈现出显著性(P>0.05),或载荷系数过低,则可考虑对其进行删除再尝试进行分析。
表3 模型拟合指标
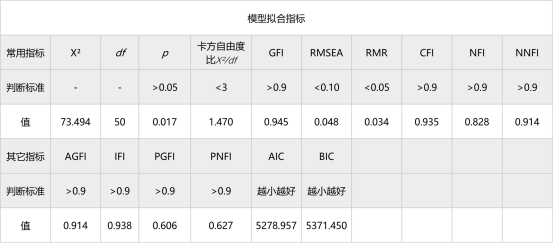
表3提供了多种常见模型拟合指标。如果多项指标能够标准,即可接受代表模型构建良好。建议结合SPSSAU提供的分析建议按步分析。

表4 MI指标表格
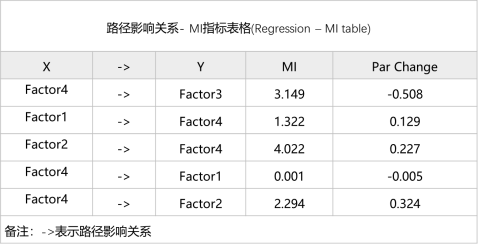
表4展示影响关系路径的MI指标值。MI指标值越大,意味着对模型调整优化帮助越大,一般情况下如果MI值大于20,此时可考虑进行修正。
表5 协方差关系表
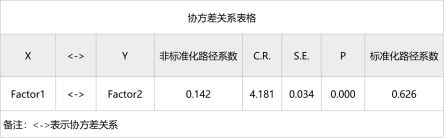
表5展示变量之间协方差关系情况。如果2个因子(潜在变量)间存在较强的相关关系,则SPSSAU会自动建立协方差关系。上表中显示Factor1和Factor2两个因子间的相关系数为0.626,并称显出显著性水平,因此自动建立协方差关系。
⑤模型修正
如果对模型进行检验时有发现拟合效果不佳时,此时有两种调整模型的办法,分别是‘影响关系调整’和‘协方差关系自动调整’。
‘影响关系调整’需要结合专业知识和MI指标进行调整,即重新在模型中加入影响关系,此种调整的目的是在于调整‘影响关系结构’;‘协方差关系自动调整’是指设置参数,让SPSSAU结合参数设置调整协方差关系,此种调整的目的是在于调整‘测量关系结构’。
最终模型结果呈现在结构图上,如下图所示:
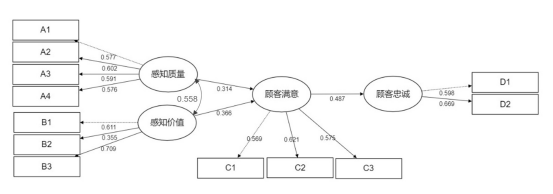
4、其他说明
如果模型无论如何拟合效果均不好,可有三种解决办法:
第一种处理是将结构方程模型进行拆分成多个小模型分别进行分析;复杂越复杂拟合越难,因此将模型的复杂度减低可有效提高拟合效果;
第二种处理是改为路径分析(即直接放弃掉测量关系进行多元模型构建,尤其是测量关系质量不佳时);
第三种处理是使用线性回归这种复杂度最低的模型进行研究。
更多内容登录SPSSAU官网查看:
SPSSAU-在线SPSS分析软件www.spssau.com?100001000
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容








所有评论(0)