矩阵定义

直接输入法

A=[1 2 3;4 5 6;7 8 9]

矩阵用方括号 “[ ]” 括起
矩阵同一行中的元素之间用 空格 或 逗号 分隔
矩阵行与行之间用 分号 分开
直接输入法中，分号可以用 回车 代替

A=[1 2 3
4 5 6
7 8 9;1 2 3]

由向量生成

通过编写m文件生成

利用MATLAB函数创建矩阵

基本矩阵函数如下：

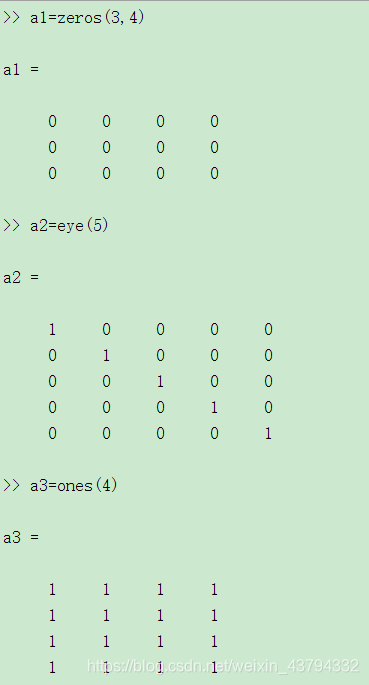
(1) ones()函数：产生全为1的矩阵，ones(n)：产生nn维的全1矩阵，ones(m,n)：产生mn维的全1矩阵；

(2) zeros()函数：产生全为0的矩阵；

(3) rand()函数：产生在（0，1）区间均匀分布的随机阵；

(4) eye()函数：产生单位阵；

(5) randn()函数：产生均值为0，方差为1的标准正态分布随机矩阵。

(6)tril()下三角矩阵

(7)triu()上三角矩阵

(8)diag（X）：若 X 是矩阵，则 diag(X) 为 X 的主对角线向量
若 X 是向量，diag(X) 产生以 X 为主对角线的对角矩阵
diag(X,k)是提取第k条对角线的元素

使用格式

A=zeros(N) 产生NN的全零矩阵
A=zeros(M,N) 产生MN的全零矩阵
A=zeros(M,N,P,…)产生MNP*…的全零矩阵
A=zeros(siza(b)) 产生和矩阵B维数相同的全零矩阵
生成五阶的随机矩阵，元素在10到90之间

矩阵元素赋值

矩阵元素可以是任何形式的表达

x=[-1.3,sqrt(3),(1+2+3)*4/5]

矩阵元素的单独赋值

x(5)=abs(x(1))

Matlab自动将向量 x 的长度扩展到 5，
并将未赋值部分置零。

大矩阵可以把小矩阵作为其元素

A=[A;11 12 13]

矩阵元素的引用

单个元素的引用
x(i)向量x中的第i个元素
A(i,j)矩阵A中的第i行，第j列元素

多个元素的引用：冒号的特殊用法
产生一个由等差序列组成的向量； a 是首项，b 是公差，c 确定最后一项；若 b=1，则 b 可以省略。
A(i:j, m:n) 表示由矩阵 A 的第 i 到第 j 行和第 m 到第 n
列交叉线上的元素组成的子矩阵。
可利用冒号提取矩阵 的整行或整列。

用于专门学科的特殊矩阵

矩阵操作

提取矩阵的部分元素： 冒号运算符

A( : )	A的所有元素
A(: , : )	二维矩阵A的所有元素
A(:,k)	A的第K列
A（k,:）	A的第k行
A（k:m）	A的第k个元素到第m个元素
A(:,k:m)	A的第 k 到第 m 列组成的子矩阵

矩阵的旋转

fliplr(A)	左右翻转
flipud(A)	上下翻转
rot90(A)	逆时针旋转90度
rot90(A,k)	逆时针旋转k*90度

矩阵转置与共轭转置

把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵，这一过程称为矩阵的转置。

矩阵 A 的共轭转置A * 定义为:将矩阵A 的行与列对换，且在将行与列对换时还要将每个元素换成该元素的共轭。

’	共轭转置
.’	转置，矩阵元素不能取共轭

点与单引号之间不能有空格

矩阵的逆和伪逆

对于一个方阵A,如果存在一个与之同阶方针B，使得AB=BA=E,此时矩阵B为A的逆矩阵，A也是B的逆矩阵，使用函数inv(A)
矩阵的伪逆如果矩阵A不是一个方阵，或者A是一个非满秩的方阵时，矩阵A没有逆矩阵，但可以找到一个与A的转置矩阵A’同型的矩阵B，使得：ABA=A，BAB=B 此时称矩阵B为矩阵A的伪逆，也称为广义逆矩阵。在MATLAB中，求一个矩阵伪逆的函数是pinv(A)。

改变矩阵的形状

reshape(A,m,n)

将矩阵元素按 列方向 进行重组,重组后得到的新矩阵的元素个数必须与原矩阵元素个数相等！

查看矩阵的大小

size(A)	列出矩阵的行数和列数
size(A，1）	返回矩阵的行数
size（A,2）	返回矩阵的列数
length(A)	等价于max(size(A))

矩阵的行列式

把一个方阵看作一个行列式，并对其按行列式的规则求值，这个值就称为矩阵所对应的行列式的值。在MATLAB中，求方阵A所对应的行列式的值的函数是det(A)。

矩阵的秩与迹

矩阵的秩 矩阵线性无关的行数与列数称为矩阵的秩。在MATLAB中，求矩阵秩的函数是rank(A)。

矩阵的迹矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和。在MATLAB中，求矩阵的迹的函数是trace(A)。

向量和矩阵的范数

矩阵或向量的范数用来度量矩阵或向量在某种意义下的长度。范数有多种方法定义，其定义不同，范数值也就不同。

(1) 向量的3种常用范数及其计算函数 在MATLAB中，求向量范数的函数为：

a、norm(V)或norm(V,2)：计算向量V的2-范数；

b、norm(V,1)：计算向量V的1-范数；

c、norm(V,inf)：计算向量V的∞-范数。

(2) 矩阵的范数及其计算函数 MATLAB提供了求3种矩阵范数的函数，其函数调用格式与求向量的范数的函数完全相同。

(3) 矩阵的条件数 在MATLAB中，计算矩阵A的3种条件数的函数是：

a、cond(A,1) 计算A的1-范数下的条件数；

b、cond(A)或cond(A,2) 计算A的2-范数数下的条件数；

c、cond(A,inf) 计算A的 ∞-范数下的条件数。

矩阵的特征值与特征

向量在MATLAB中，计算矩阵A的特征值和特征向量的函数是eig(A)，常用的调用格式有3种：

(1) E=eig(A)：求矩阵A的全部特征值，构成向量E。

(2) [V,D]=eig(A)：求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量。

(3) [V,D]=eig(A,’nobalance’)：与第2种格式类似，但第2种格式中先对A作相似变换后求矩阵A的特征值和特征向量，而格式3直接求矩阵A的特征值和特征向量。

矩阵的基本运算

矩阵的加减

对应分量进行运算，要求参与加减运算的矩阵具有 相同的维数

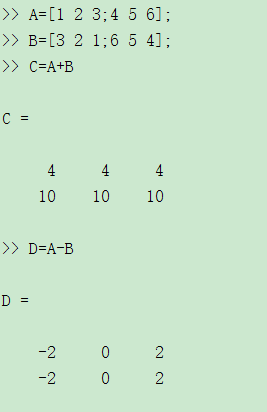
矩阵的普通乘法

矩阵的除法

矩阵的乘法

A 是方阵，p 是正整数
A^p 表示 A 的 p 次幂，即 p 个 A 相乘。

若 A 是方阵，p 不是正整数
A^p 的计算涉及到 A 的特征值分解，即若
A = VDV-1
则 A^p=V*(D.p)/V

矩阵的 Kronecker 乘积

矩阵的数组运算

数组运算：对应元素进行运算
数组运算包括：点乘、点除、点幂
相应的数组运算符为： “.* ” ， “./ ” ， “.\ ” 和“ .^ ”
点与算术运算符之间不能有空格！

矩阵中所有元素

矩阵所有元素求和

sum(A)	对矩阵每一列的元素分别求和
sum(A,2)	对矩阵每一行的元素分别求和
sum(A(😃)	将矩阵的所有元素相加求和

求期望

mean(A)	对矩阵每一列的元素分别求期望
mean(A,2)	对矩阵每一行的元素分别求期望
mean(A(😃)	将矩阵的所有元素相加求期望

求均方差

std2（A）:求矩阵所有元素的均方差

矩阵与数的运算

加减：矩阵的每个元素都与数作加减运算

数乘：矩阵的每个元素都与数作乘法运算

矩阵除以一个数：每个元素都除以这个数

点幂：
底为矩阵，指数为标量
底为标量，指数为矩阵

稀疏矩阵

MATLAB的矩阵有两种存储方式：完全存储方式和稀疏存储方式。

完全存储方式

完全存储方式是将矩阵的全部元素按列存储。以前讲到的矩阵的存储方式都是按这个方式存储的，此存储方式对稀疏矩阵也适用。

稀疏存储方式

稀疏存储方式仅存储矩阵所有的非零元素的值及其位置，即行号和列号。在MATLAB中，稀疏存储方式也是按列存储的。
注意，在讲稀疏矩阵时，有两个不同的概念，一是指矩阵的0元素较多，该矩阵是一个具有稀疏特征的矩阵，二是指采用稀疏方式存储的矩阵。

sparse(S)

将矩阵S转化为稀疏存储方式。当矩阵S已经是稀疏存储方式时，则函数调用相当于ans=S。
例如

sparse函数还有其他一些调用格式：sparse(m,n)：生成一个m×n的所有元素都是0的稀疏矩阵。
sparse(u,v,s,m,n)：u,v,s是3个等长的向量
s是要建立的稀疏矩阵的非0元素
u(i)、v(i)分别是s(i)的行和列标
m,n分别是矩阵的行数和列数。当m,n未被指定时，该函数建立一个max(u)行、max(v)列并以s为稀疏元素的稀疏矩阵
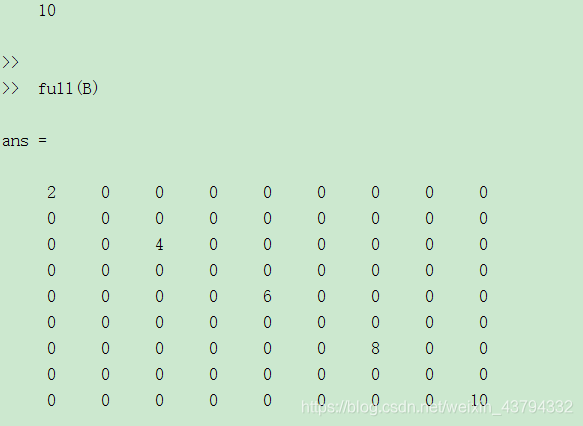
还有一些和稀疏矩阵操作有关的函数。例如[u,v,s]=find(A)：返回矩阵A中非0元素及下标。产生的u,v,s可作为sparse(u,v,s)的参数。full(A)：返回和稀疏存储矩阵A对应的完全存储方式矩阵。

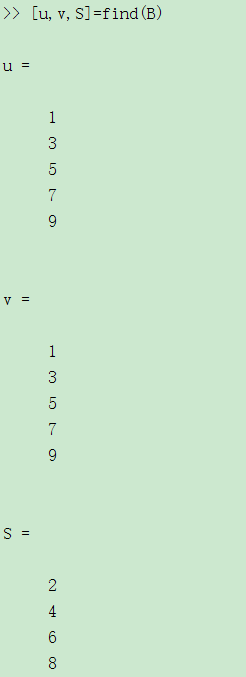
特殊稀疏矩阵

单位矩阵只有对角线元素为1，其他元素都是0，是一种具有稀疏特征的矩阵。
函数eye产生一个完全存储方式的单位矩阵。
函数speye(m,n)返回一个m×n的稀疏存储方式的单位矩阵。若m=n可简写为speye(n)。
spones(S):把矩阵S的非零元素值改为1。
sprand：产生非零元素为均匀分布的随机数的稀疏矩阵 。

稀疏存储矩阵只是矩阵的存储方式不同，它的运算规则与普通矩阵是一样的。所以，在运算过程中，稀疏存储矩阵可以直接参与运算。当参与运算的对象不全是稀疏存储矩阵时，所得结果一般是完全存储形式。