微分方程的解析解

求微分方程（组）的解析解命令：

dsolve('方程1','方程2',...'方程n','初始条件','自变量')

注：字母D表示求微分，D2、D3等表示求高阶微分，D后所跟的字母为因变量，自变量可以指定或由系统规则选定为缺省，默认是以t为自变量。
如，微分方程d²y/dx² =0 应表达为：D2y=0

例1：求 du/dt=1+u²的通解。
输入命令：dsolve(‘Du=1+u^2’,‘t’)
运行结果：u=tan(t-c)

输入命令y=dsolve('D2y+4*Dy+29*y=0','y(0)=0,Dy(0)=15','x')
运行结果为y =3sin(5x)exp(-2x)

输入命令：[x,y,z]=dsolve('Dx=2*x-3*y+3*z','Dy=4*x-5*y+3*z','Dz=4*x-4*y+2*z','t')
运行结果为：
x = C3exp(2t) + C4exp(-t)
y = C3exp(2t) + C4exp(-t) + C5exp(-2t)
z = C3exp(2t) + C5exp(-2t)

以上都是常微分方程的精确解法，也称为常微分方程的符号解。但是，我们知道，有大量的常微分方程虽然从理论上讲，其解是存在的，但我们却无法求出其解析解，此时，我们需要寻求方程的数值解。

用MATLAB求微分方程的数值解

在求解常微分方程数值解方面，MATLAB具有丰富的函数，我们统称为solver，其一般格式为：

参数说明：
t是时间点组成的列向量；
x是微分方程（组）的解矩阵，每一行对应相应t的该行上时间点的微分方程（组）的解；
ts有两种形式 [t0,tf] 和[t0,t1,…tf]，两种都以 t0 为初始点，根据 tf 自动选择积分步长。前者返回实际求解过程中所有求解的时间点上的解，而后者只返回设定时间点上的解。后者对计算效率没有太大影响，但是求解大型问题时，可以减少内存存储。
solver为命令 ode45,ode23,ode113,ode15s,ode23s,ode23t,ode23tb之一，其中前3个适用于求解非刚性（Nonstiff）问题，后4个适用于刚性问题。这些命令各有特点，列表说明：

求解器	ODE类型	特点	说明
ode45	非刚性	一步算法，4，5阶Runge-Kutta方法累积截断误差(△x)3	大部分场合的首选算法
ode23	非刚性	一步算法，2，3阶Runge-Kutta方法累积截断误差(△x)3	使用于精度较低的情形
ode113	非刚性	多步算法，Adam算法，高低精度均可达到 10-3~10-6	计算时间比ode45短
ode23t	适度刚性	采用梯形算法	适度刚性情形
ode15s	刚性	多步法，Gear’s 反向数值积分，精度中等	若ode45失效时，可尝试使用
ode23s	刚性	一步法，2阶Rosebrock算法，低精度	当精度较低时，计算时间比ode15s短
ode23tb	刚性	梯形算法，低精度	当精度较低时，计算时间比ode15s短

例4：求解常微分方程 y’=-2y+2x²+2x，0<=x<=0.5，y(0)=1的程序如下：fun=inline(’-2y+2xx+2x’); [x,y]=ode23(fun,[0,0.5],1)
结果为：
x =
0, 0.0400,0.0900,0.1400,0.1900,0.2400,0.2900,0.3400,0.390,0.4400,0.4900,0.5000
y =
1.0000,0.9247,0.8434,0.7754,0.7199,0.6764,0.6440,0.6222,0.6105,0.6084,0.6154,0.6179

例5：求解常微分方程的解.
分析：这是一个二阶非线性方程，用现成的方法均不能求解，但我们可以通过下面的变换，将二阶方程化为一阶方程，即可求解，这种方法是打靶法。
令：x1=y, x2=dy/dt , u=7，则得到：

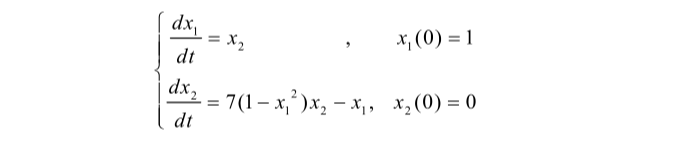
接着，编写vdp.m如下：

//新建函数vdp，并保存在vdp.m文件中
function fy=vdp(t,x)	
fy=[x(2);7*(1-x(1)^2)*x(2)-x(1)];	//矩阵

再编写m文件sy12_6.m如下：

//调用ode算法来求解
y0=[1;0];	//初始条件
[t,x]=ode45(@vdp,[0,40],y0);
plot(t,x(:,1),t,x(:,2))	%分别画出x数组第一列和第二列的数随t的变化曲线

运行结果：

上机题：

程序：dsolve('D3y-D2y-3*Dy+2*y','x')


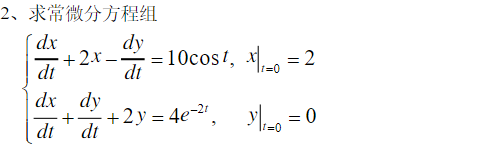
程序：[x,y]=dsolve('Dx=5*cos(t)+2*exp(-2*t)-x-y','Dy=-5*cos(t)+2*exp(-2*t)+x-y','x(0)=2,y(0)=0','t')

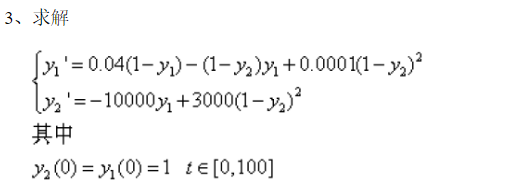
用ode45函数求解，并画出图形。
建立f2.m文件，

function dx=f2(t,y)
dx=zeros(2,1);	%初始化dx为两行一列的矩阵
dx(1)=0.04*(1-y(1))-(1-y(2))*y(1)+0.0001*(1-y(2))^2;
dx(2)=-10000*y(1)+3000*(1-y(2))^2;

利用ode45算法求解，建立f3.m文件，

[t,x]=ode45('f2',[0 100],[1 1]);
plot(t,x(:,1),'+',t,x(:,2),'*');

程序：
求解析解：y=dsolve('Dy=-y+t+1','y(0)=1','t')结果为：y =t + exp(-t)
在[0,1]上作图：

ezplot('t + exp(-t)',[0,1])
title('t + exp(-t)')

用ode45求数值解：

%f2.m
function dy=f2(t,y)
dy=zeros(1,1);
dy(1)=-y(1)+t+1;

%f3.m
[t,y]=ode45('f2',[0 1],[1]);
plot(t,y,'ro');
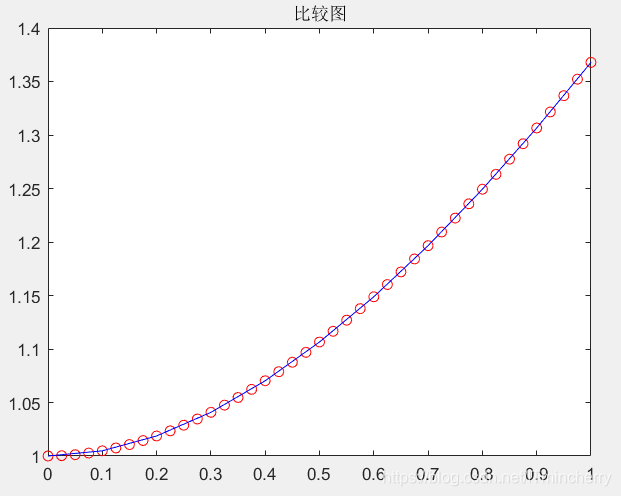
title('比较图');

在同一幅图中比较：

[t,y]=ode45('f2',[0 1],[1]);
plot(t,y,'ro');
title('比较图');
t=0:0.1:1;
y=t+exp(-t);
hold on
plot(t,y,'b');