机器人学中的状态估计——学习笔记
机器人学中的状态估计——学习笔记离散时间的批量估计问题1、最大后验概率法(Maximum A Posteriori, MAP)2、贝叶斯推断(Bayesian inference)离散时间的迭代平滑问题1、Cholesky平滑算法2、Rauch-Tung-Striebel 平滑算法离散时间的迭代滤波问题离散时间的批量估计问题问题描述:在离散线性高斯模型下,利用所有时刻的数据估计某一时刻的状态。..
机器人学中的状态估计——学习笔记
离散时间的批量估计问题
问题描述:在离散线性高斯模型下,利用所有时刻的数据估计某一时刻的状态。
符号:

方法:
1、最大后验概率法(Maximum A Posteriori, MAP)
x
^
=
arg
max
x
p
(
x
∣
v
,
y
)
\hat{\boldsymbol{x}}=\arg \max _{\boldsymbol{x}} p(\boldsymbol{x} | \boldsymbol{v}, \boldsymbol{y})
x^=argxmaxp(x∣v,y)
where
x
=
x
0
:
K
=
(
x
0
,
…
,
x
K
)
,
v
=
(
x
ˇ
0
,
v
1
:
K
)
,
y
=
y
0
:
K
=
(
y
0
,
…
,
y
K
)
\boldsymbol{x}=\boldsymbol{x}_{0: K}=\left(\boldsymbol{x}_{0}, \ldots, \boldsymbol{x}_{K}\right), \quad \boldsymbol{v}=\left(\check{\boldsymbol{x}}_{0}, \boldsymbol{v}_{1: K}\right), \quad \boldsymbol{y}=\boldsymbol{y}_{0: K}=\left(\boldsymbol{y}_{0}, \ldots, \boldsymbol{y}_{K}\right)
x=x0:K=(x0,…,xK),v=(xˇ0,v1:K),y=y0:K=(y0,…,yK)
Note:
p
p
p是概率密度函数,不是概率。
重要步骤:
- 由贝叶斯公式得:
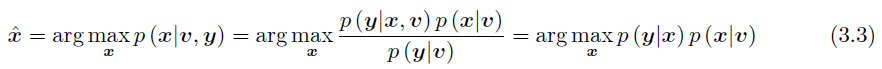
- 由于噪声之间相互独立(假设1):

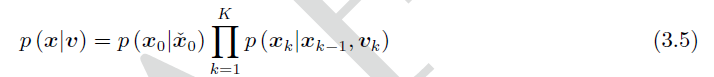
因此,(3.3)式被分解成了三个式子。
- 用条件高斯分布公式分别求解以上三个式子。这一步能够引出
c
o
s
t
f
u
n
c
t
i
o
n
cost function
costfunction
先给出条件高斯分布公式:
对于联合概率分布是高斯分布 p ( x a , x b ) p(x_{a},x_{b}) p(xa,xb)的两个变量,其条件高斯分布 p ( x a ∣ x b ) p\left(x_{a} | x_{b}\right) p(xa∣xb)和边缘分布 1 ^1 1都是高斯分布,其中 p ( x a ∣ x b ) p\left(x_{a} | x_{b}\right) p(xa∣xb)的均值和协方差矩阵的公式为:
μ a l b = μ a + Σ a b Σ b b − 1 ( x b − μ b ) Σ a ∣ b = Σ a a − Σ a b Σ b b − 1 Σ b a \begin{aligned} \mu_{\mathrm{alb}} &=\mu_{a}+\Sigma_{a b} \Sigma_{b b}^{-1}\left(x_{b}-\mu_{b}\right) \\ \Sigma_{a | b} &=\Sigma_{a a}-\Sigma_{a b} \Sigma_{b b}^{-1} \Sigma_{b a} \end{aligned} μalbΣa∣b=μa+ΣabΣbb−1(xb−μb)=Σaa−ΣabΣbb−1Σba
1、 边缘分布(Marginal Distribution)指在概率论和统计学的多维随机变量中,只包含其中部分变量的概率分布。
那么, 对(3.3)等式右端取对数,并假设 P ˇ 0 , Q k \check{P}_{0}, Q_{k} Pˇ0,Qk和 R k R_{k} Rk都是可逆的(假设2),可得:
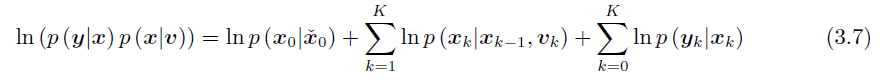
化简掉与 x x x无关的 l n ( ⋅ ) ln(\cdot) ln(⋅)项,可得:
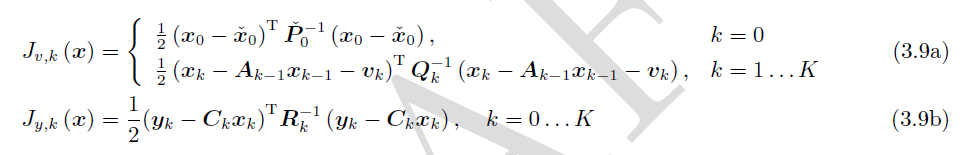
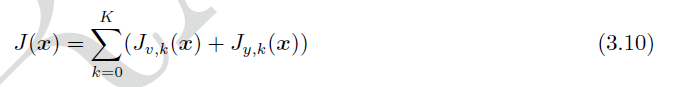
最终将原始问题化成了:

将以上式子化成矩阵形式:

求偏导:
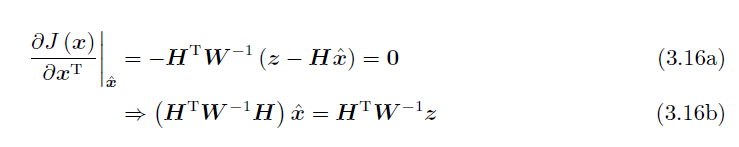
最终结果如上。
2、贝叶斯推断(Bayesian inference)
暂略。
离散时间的迭代平滑问题
某些叫法:矩阵有稀疏结构,代表他含有对角块,如:

本节内容的目的:上一节虽然能得到最优解,但是效率很低,因为要求矩阵的逆等等。因此,可以利用矩阵稀疏结构加速求解。采用的方法:一次前向递推和一次后向地推,称为固定区间平滑算法。
本节的问题:利用稀疏矩阵的特性求解方程:
(
H
T
W
−
1
H
)
x
^
=
H
T
W
−
1
z
\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{W}^{-1} \boldsymbol{H}\right) \hat{\boldsymbol{x}}=\boldsymbol{H}^{\mathrm{T}} \boldsymbol{W}^{-1} \boldsymbol{z}
(HTW−1H)x^=HTW−1z
1、Cholesky平滑算法
步骤:
- 利用稀疏Cholesky分解可得:
H T W − 1 H = L L T \boldsymbol{H}^{\mathrm{T}} \boldsymbol{W}^{-1} \boldsymbol{H}=\boldsymbol{L} \boldsymbol{L}^{\mathrm{T}} HTW−1H=LLT
其中,

下面首先利用前向迭代求解其中的每一个小矩阵: - 由
H
T
W
−
1
H
=
L
L
T
\boldsymbol{H}^{\mathrm{T}} \boldsymbol{W}^{-1} \boldsymbol{H}=\boldsymbol{L} \boldsymbol{L}^{\mathrm{T}}
HTW−1H=LLT得:

先求 L 0 L_{0} L0,这需要利用一次⼩型块的稠密矩阵分解。然后一项一项地求,可得到 L L L。 - 由上可得,
L
L
T
x
^
=
H
T
W
−
1
z
LL^{T}\hat{x} = H^{T}W^{-1}z
LLTx^=HTW−1z, 令
L
T
x
^
=
d
L^{T}\hat{x} = d
LTx^=d, 那么先计算
d
d
d:
用类似的方法:

一项一项求解 d 0 , . . . , d K d_{0},...,d_{K} d0,...,dK。 - 最后求解:
L
T
x
^
=
d
L^{\mathrm{T}} \hat{x}=d
LTx^=d,展开后:

先求 x ^ K \hat{\boldsymbol{x}}_{K} x^K,一项一项求解,称为逆向迭代。
总结:

初值:
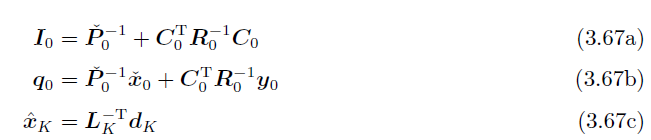
其中的五个向前迭代又是***卡尔曼滤波***。
2、Rauch-Tung-Striebel 平滑算法
该算法是Cholesky平滑算法的标准形式,更接近于我们平时用的卡尔曼滤波。
离散时间的迭代滤波问题
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)