普通条幅波AM可以用包络检波来得到中频信号

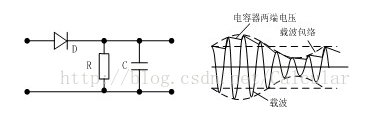
下面是包络检波电路：

注意：上图电路中经推算输入电阻约等于R/2 （左端电压除以流经二极管的电流）

基本原理：左端输入电压正向作用于二极管时，电流经过电阻R流入地（一切正常）同时R两端的电压又给电容器充电，当反向电压作用于二极管时，电流不能通过，此时已充满电的电容开始放电了，放电的速度和时间常数=R*C有关，当R*C远大于高频频率的倒数时（就是最短周期），就可以滤除高频分量。

在右图中可以看出充电速度明显快于放电速度，每当信号电压将要大于电容两端电压的时候，电容将要充电，而每当信号电压将要小于电容两端电压的时候，电容将要放电，放电速度取决于R*C

设输入的调幅波AM信号为：

vi(t)=Vcm*(1+ma*cos(w1*t))*cos(w2*t)

其中，Vcm为载波幅度值，ma为条幅系数（ma<1），w1为低频信号角频率，w2为高频载波角频率。

当输入为小信号时（<100mV）为保证二极管导通，应加偏置电压Vq，此时二极管的非线性特性可以用幂级数来逼近，当输入为大信号时，可以用两段折线来描述（包络前者是光滑的后者是折线）

 

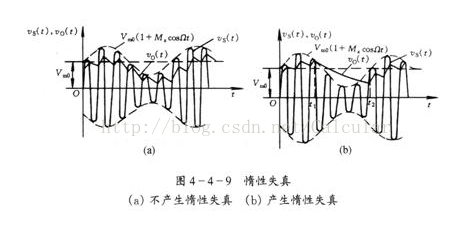
当输入为大信号时有以下两种失真

为不产生如下惰性失真，R*C不能太大

在输入信号幅度下降的任何时候都应满足电容器通过R的放电速度大于包络下降的速度。

经推导必须满足如下式子：

R*C<=sqrt(1-ma^2)/(w1*ma)   其中sqrt()为平方根，ma为调幅系数，w1为包络角频率（低频）

当然另有 5~10/w2<=R*C 其中5~10为估计值，w2为高频率载波角频率

角频率w=2*pi*f 这个不用多说，f为频率

 

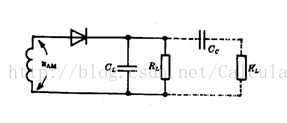
同时，为了去除直流影响，检波器与下一级间采用加隔直流电容的交流耦合方式

为了不产生负峰切割失真，还必须满足：

ma*(R=/R~)<1

其中R=为从电容往右看去的直流总电阻，R~为交流总电阻

如上图中R=为Rl，R~为Rl//R`l

 

性能指标：

动态检波效率 kd=Vav/(Vcm*ma)    表示 输出交流幅度与输入信号包络幅度之比

检波器从信号源吸取的功率 Pi=0.5*Vcm^2/Ri    其中Ri为输入电阻

输出到负载R上的功率 Po=Vav^2/R 在输入大信号时(峰值包络检波)kd约为1 所以Po=Vcm^2/R